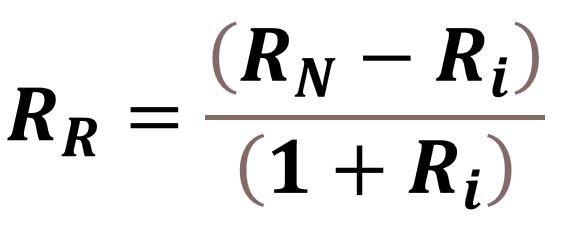Inflation Rates, Real Returns and Nominal Returns 

Inflation Rates, Real Returns and Nominal Returns

Last Update: February 14, 2024 

Inflation

Let’s derive an equation showing the relationship between Real Returns and Nominal Returns. But first, we need to define what economic inflation means. 

Inflation is the general increase in price levels. Inflation could be caused by central bank monetary policies like reducing interest rates or increasing the money supply. Other factors like supply chain shocks could contribute to inflation as well.   

To differentiate growth due to the overall increase in price levels from other factors , like

• increases in capital goods,
• improvements in technology,
• increases in the labor force or
• improvement in labor force productivity (output/hours worked),

we can define two types of return: The Nominal Return and the Real Return. 

Nominal Returns and Real Returns

• A Nominal Return is the actual all inclusive return. It includes the impact of inflation (general increase in prices). 
• The Real Return is the Nominal Return without the the effects of inflation; it is the inflation adjusted return.
• Not 100% accurately (more on this in the next section), Nominal Rate – Inflation Rate ≅ Real Rate.
• For example a 10% nominal rate with an inflation rate of 4% gives you, approximately, a 6% Real Rate. 
• The Real Rate can be described as a Constant Dollar Rate, meaning it reflects growth that doesn’t include changes in prices (i.e. we are fixing the purchasing power of the dollar so  prices are constant). 
• In the example above, the 6% Real Rate compared to the 10% nominal rate reflects the loss of purchasing power of your dollars (i.e. the inflation rate). In absolute terms the purchasing power is still positive though.  
• Nominal and Real GDP can be described the same way where,  
• Real GDP = (Nominal GDP in year Y ) x (Baseline Price Basis Defined as 100)/(Price relative to basis in year Y) 

Nominal Rate and Real Rate Relationships

Let’s develop a more rigorous relationship between the Nominal and Real Rates.

1.  We can Approximate the Real Return as Nominal Return – Inflation Rate  e.g. A 10% nominal return with 3.5% inflation would produce a Real Return of 6.5%.    

To be a little more rigorous, let

• FV = Future Value
• PV = Present Value
• n = number of years 
• R_R = Real Return (does not include inflation)
• R_i = Inflation rate
• R_N = Nominal Return (the actual return, which includes inflation)

The lump sum or single sum compounding equation is,

2. FV = PV(1+Rate)ⁿ

We can express the growth factor (1+Rate)ⁿ  as the product of an inflation growth factor and a real growth factor:

3. FV =   PV (1+R_i)ⁿ(1+R_R)ⁿ  which can be expressed as

4. FV =   PV ( (1+R_i)(1+R_R))ⁿ 

Define the Nominal Rate R_N  which reflects the actual or total rate. 

5. FV = PV (1+R_N)ⁿ 

We can express the equality of equations 4. and 5. as equation 6.

6. (1+R_N) = (1+R_i)(1+R_R)

Finally, Equation 6. can be expressed as equations 7. , 8. and 9.

Primary Relationships between Inflation, Real, and Nominal Rates

7. R_i = [(1+R_N)/(1+R_R)] – 1

8. R_R = [(1+R_N)/(1+R_i)] – 1 = (R_N–R_i)/(1+R_i)

9. R_N = [(1+R_i)(1+R_R)] – 1

Lets go back to the 10% nominal return with 3.5% inflation example. We said that the difference was the Real Return of 6.5%. But lets apply equation 8. to get the rigorous answer: 

R_R = [(1+10%)/(1+3.5%)] – 1 = 6.28%. 

This is not far off in absolute terms from our 6.5% estimate, but you need to be as accurate as possible, because over long periods of time, small differences in growth rates can result in very large outcomes (see my power of compounding post) . 

Example 1

Your investment returns 10% in 2022. What is the inflation adjusted rate of return if inflation ran at 7% in 2022?

R_R = [(1+R_N)/(1+R_i)] – 1 = (1.10)/(1.07)-1 = 2.8%.  

The Real Rate of Return is 2.8%. 

Example 2

A bond pays you 4.5 % per year. If the inflation rate is currently 7% per year, then the real return is actually negative: 

R_R =  (1.045)/(1.05)-1 = -2.34%. 

In this case the loss in purchasing power results in a loss in your real wealth. 

Example 3

A Real Rate of Return can be used in college (or other) tuition funding calculations where the desire is to compute an equivalent lump sum payment in the first year of college given a 1st year payment and given a tuition increase that occurs each year of the four years. 

For example, if you expect to earn 7% on your investments but college tuition is going to increase 6% per year, the rate of return in this calculation would be 

(1.07)/(1.10)-1 = .94%