Menu (linked Index)
Vector Math
Last Update: August 12, 2025
Introduction
Vectors are mathematical constructs that indicate magnitude and time.
They are very useful in science and engineering fields.
In this post, we’ll cover the basic math of vectors.
Vectors and Scalars
- Intro vectors 1 ; Intro vectors 2 (khanacademy.org)
- Adding vectors (khanacademy.org); Subtracting vectors
- Multiplying a vector by a scalar (khanacademy.org)
- Vector dot product and vector length (khanacademy.org)
- Vector Cross product introduction (khanacademy.org)
Scalar
A scalar only has magnitude (size).
Example: Speed
Vector
A vector has magnitude (size) and direction.
Example: Velocity = Speed in a specified direction
Example: Force has magnitude and direction
Vectors Are not Defined by the Position of the Tail
Vectors have magnitude and direction but graphically they don’t specifically place anywhere.
- Vectors are not uniquely fixed on a coordinate space because they represent a magnitude and direction, not a specific starting point.
- The same vector can be drawn starting from any point in the coordinate system, as long as its length and direction remain unchanged.
The Unit Vector
Unit vectors are dimensionless vectors of magnitude 1 unit.
They specify the direction of a vector on a Cartesian (x,y,z etc.) coordinate system and are usually symbolized by the letter i, j, k with a circumflex on top:
- î : unit vector in the x direction
- ĵ : unit vector in the y direction
- k̂ : unit vector in the z direction
These are often used to express any vector as a sum of its components.
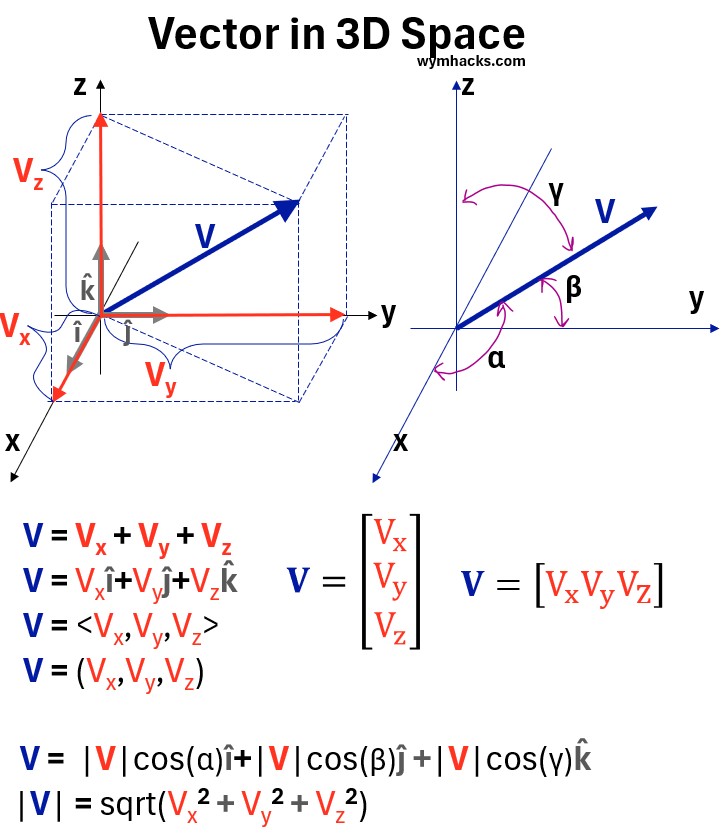
For example, a vector V in three-dimensional space can be written as:
V=Vxî + Vy ĵ + Vzk̂
Where
- Vx , Vy, Vz are the scalar components of the vector along each axis.
Since a unit vector is a vector with a magnitude (or length) of 1 , you can create a unit vector from any non-zero vector by dividing that vector by its own magnitude.
- This process is called normalization.
So, For any given vector V , its unit vector = V/|V|
- where |V| is the magnitude of vector V
Specifying (Defining a Vector)
Two Methods of Specifying a Vector
Specifying or defining a vector can be done in two ways
Consider the vector V in the drawing below.
Graph: Vector in 2D Space
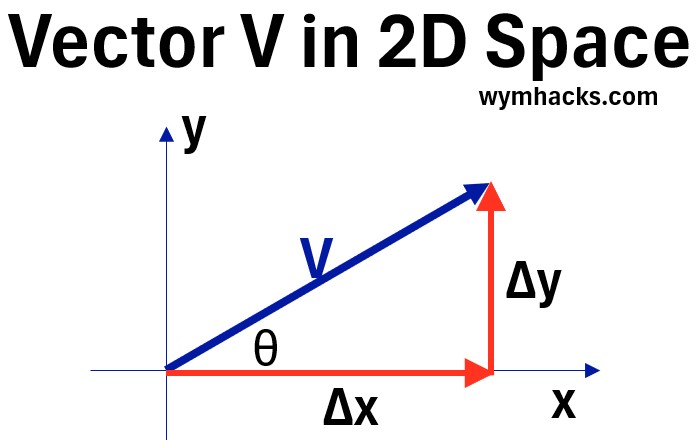
A vector can be specified by length and an angle . That is
- by the magnitude of V or |V|
- and the angle θ between V and x.
A vector can also be specified by its components. In the graph above,
- V is defined by starting at its tail and then
- moving Δx units to the right on the x axis
- and them up Δy units going up on the Y axis
- tan θ = Δy/Δx
It is true that the Vector V = Vector Δx + Vector Δy
We will learn more about addition of vectors in a following section.
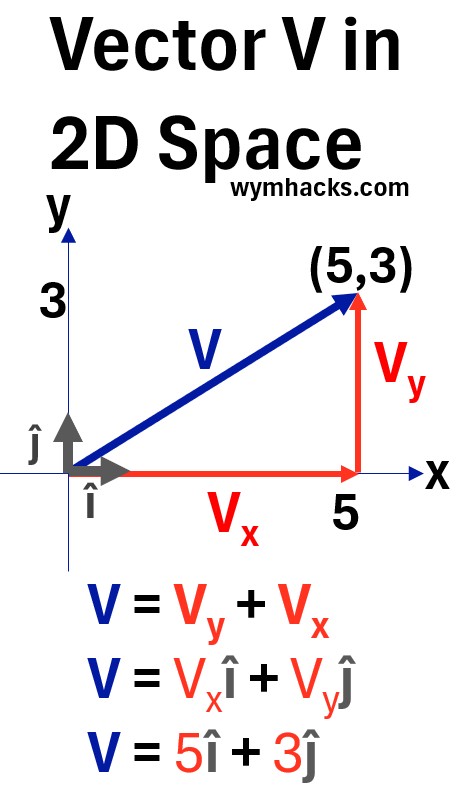
Consider the vector shown in the graph below. The unit vectors are shown as the grey arrows on the x and y axes.
Graph: Vector V in 2D Space with Unit Vectors î and ĵ
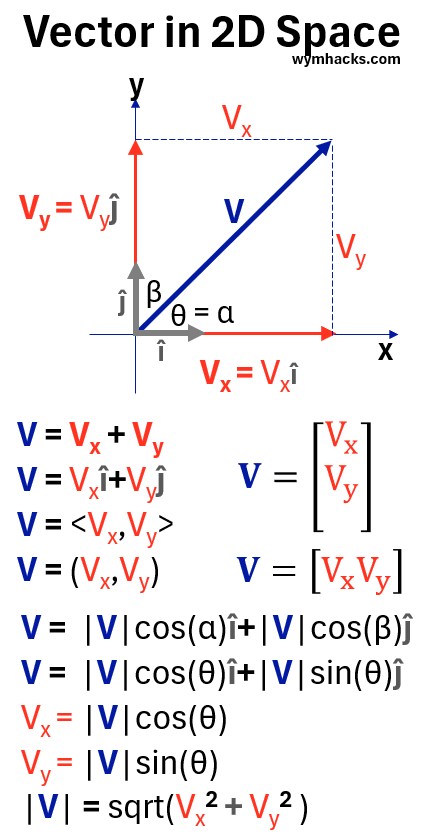
In the example above, the vector V begins at point (0,0) and is displaced to point (5,3).
We can express the vector V as follows:
- V = Vx + Vy
- these are all vectors
- V = Vx î + Vyĵ
- Un-bolded Vx and Vy are expressed as scalar multipliers of the unit vectors.
- V = 5î + 3ĵ
- i.e. A vector V is created starting at its tail; with 5 moves in the x direction (i.e. 5î) and with 3 moves in the y direction (or 3ĵ)
Another way to express a vector is with angle bracket notation (called component form).
In our example V = <5,3> where:
- This notation represents a vector in a two-dimensional plane.
- For a 3-D vector the expression is expanded to one more term.
- The numbers inside the brackets are the components of the vector, which describe its movement or direction from a starting point.
- The first component, 5, represents a movement of 5 units along the x-axis (horizontally).
- The second component, 3, represents a movement of 3 units along the y-axis (vertically).
So, the vector ⟨5,3⟩ describes a displacement that is 5 units to the right and 3 units up.
Also , the unit vectors expressed in component form would be
- î = <1,0,0>
- ĵ = <0,1,0>
- k̂ = <0,0,1>
The component format can take on a few more styles like
- Parenthesis ( ) instead of angle brackets < >
- Brackets [ ] with values in column or row, comma format
In the two graphs below, I show the basic generalized graphics, notations, and equations for a 2D and 3D vector.
Graph: Vector in 2D Space
Graph: Vector in 3D Space
Vector Addition
To add vectors algebraically, sum their corresponding components.
- If a=(ax,ay,az) and b=(bx,by,bz), then: a+b=(ax+bx,ay+by,az+bz)
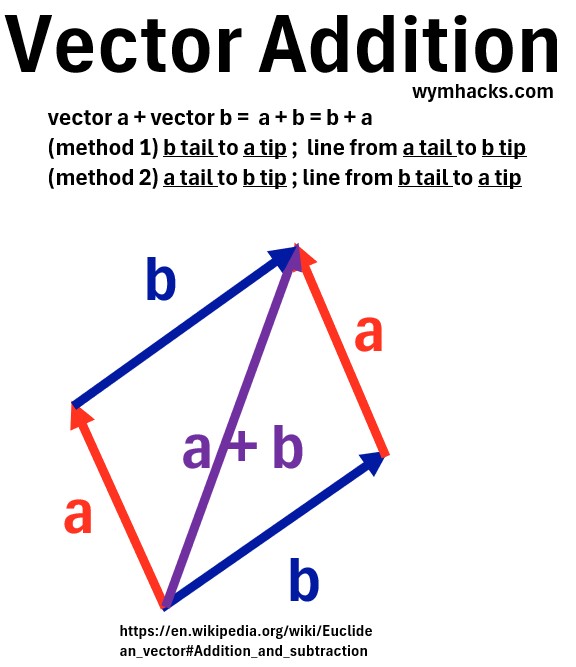
Vector Addition: Graphical (Tip-to-Tail / Triangle Rule):
- Place the tail of the second vector (b) at the tip (arrowhead) of the first vector (a).
- The resultant sum vector (a+b) is drawn from the tail of the first vector to the tip of the second vector.
Vector Addition: Graphical (Parallelogram Rule):
- Draw both vectors (a and b) with their tails at the same starting point.
- Complete the parallelogram formed by these two vectors as adjacent sides.
- The resultant sum vector (a+b) is the diagonal of the parallelogram that starts from the common tail point.
Properties of Vector Addition:
For vectors a, b, c and the zero vector 0:
- Commutativity: The order of addition does not affect the sum. a + b = b + a
- Associativity: The grouping of vectors in addition does not affect the sum. (a + b) + c = a+(b + c)
- Identity Element (Zero Vector): Adding the zero vector to any vector leaves the vector unchanged: a+0 = a
- Inverse Element (Negative Vector): For every vector a, there exists a unique negative vector (−a) such that their sum is the zero vector: a+(−a)=0
- Closure: The sum of two vectors is always another vector.
Vector Subtraction
- Subtracting vector b from vector a, (a−b), is defined as adding vector a to the negative of vector b: (a+(−b)).
- The negative vector (−b) has the same magnitude as b but points in the exact opposite direction (i.e. flipped 180 degrees).
- Subtract the corresponding components of the vectors.
- If a=(ax,ay,az) and b=(bx,by,bz), then: a−b=(ax−bx,ay−by,az−bz)
- Graphical (tip to tip): If vectors a and b are drawn with their tails at the same starting point, the resultant vector a−b is drawn from the tip of b to the tip of a.
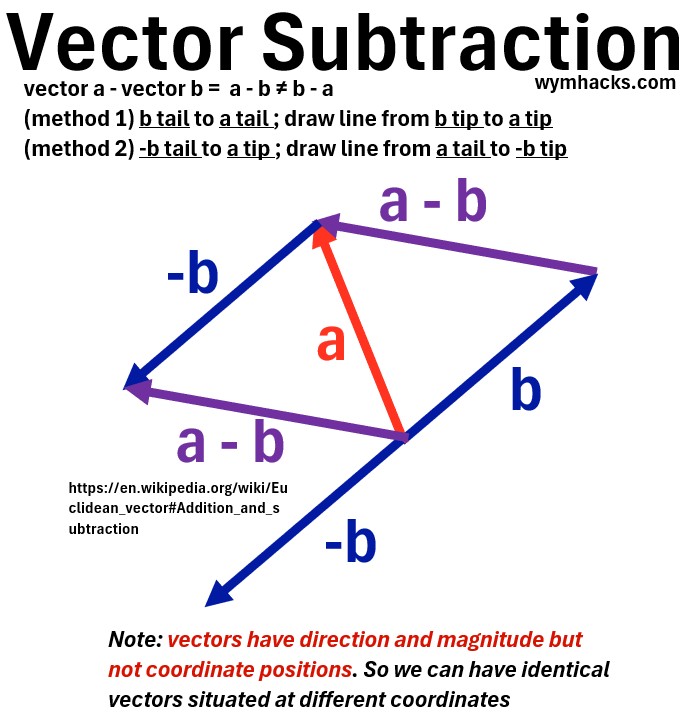
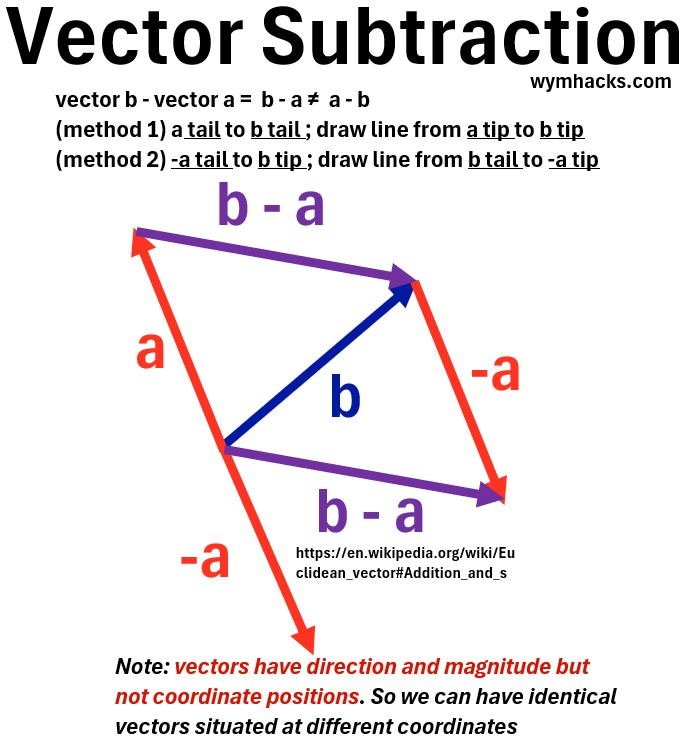
- Graphical (flip subtrahend vector and add): Flip the subtrahend vector 180 degrees and add this to the first vector
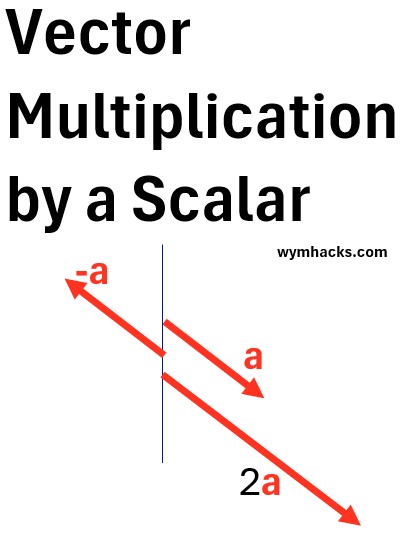
Vector Multiplication by a scalar
- Multiplying a vector by a positive scalar increases the magnitude of the vector
- Multiplying a vector by negative one, flips the direction by 180 degrees
Length (Magnitude of a vector)
The length or magnitude of a vector is a scalar quantity that represents the “size” or “extent” of the vector, without regard to its direction.
The magnitude of a vector v is typically denoted as ∥v∥ or ∣v∣.
For a vector in a coordinate system:
- In two dimensions (e.g., v=⟨x,y⟩): The magnitude is calculated using the Pythagorean theorem: ∥v∥=sqrt(x2+y2)
- In three dimensions (e.g., v=⟨x,y,z⟩): The magnitude is also found using a generalization of the Pythagorean theorem: ∥v∥=sqrt(x2+y2+z2)
This makes sense. Just plot
This concept extends to vectors in any number of dimensions, where the magnitude is the square root of the sum of the squares of all its components.
Vector Dot Product
The dot product (also known as the scalar product or inner product) of two vectors is an algebraic operation that takes two equal-length sequences of numbers (vectors) and returns a single number (a scalar).
Vector Dot Product Algebraic Definition
Given two vectors a=⟨a1,a2,…,an⟩ and b=⟨b1,b2,…,bn⟩ in n-dimensional space,
- their dot product is the sum of the products of their corresponding components:
that is, a⋅b=a1b1+a2b2+⋯+anbn=∑aibi for i = 1 to n
Vector Dot Product Geometric Definition
Given two vectors a and b in Euclidean space, their dot product is the product of their magnitudes and the cosine of the angle θ between them:
a⋅b=∣a∣∣b∣cos(θ)
- where ∣a∣ is the magnitude (length) of vector a,
- and ∣b∣ is the magnitude of vector b.
- Lower case versus bold is sometimes used to differentiate a vector from its scalar form.
- The Dot product a · b
- = scalar product of b & “the projection of a onto b” = bacos(θ)
- = scalar product of a & “the projection of b onto a” = abcos(θ)
The dot product is the product of the lengths of the vectors that are aligned in the same direction.
- The maximum value of a dot product will occur when the vectors are colinear (aligned the same way i.e. θ =0)
- When vectors a and b are perpendicular to each other, their dot product is zero (i.e. θ =90 degrees).
Picture: Geometric Interpretation of Dot Product
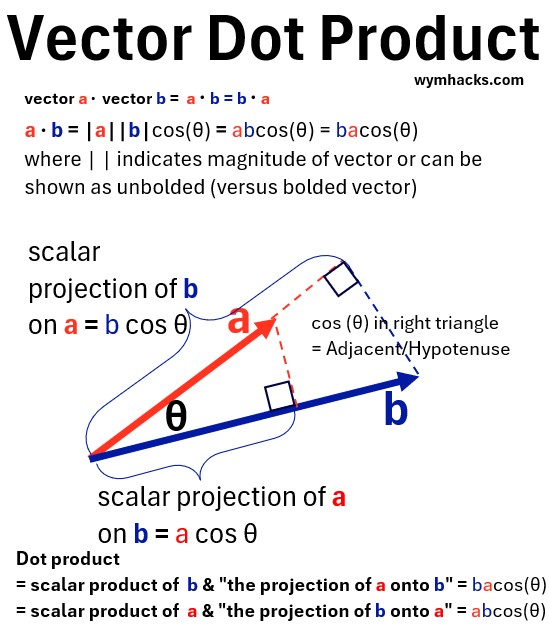
Properties of the Dot Product:
Let u, v, and w be vectors, and c be a scalar.
- Commutative Property: The order of the vectors does not affect the result. u⋅v=v⋅u
- Distributive Property over Vector Addition: u⋅(v+w)=u⋅v+u⋅w
- Scalar Multiplication Property (Associative with Scalar Multiplication): (cu)⋅v=u⋅(cv)=c(u⋅v)
- Relationship with Magnitude (Squared Length): The dot product of a vector with itself gives the square of its magnitude. u⋅u=∣u∣2 .This also implies that ∣u∣=u⋅u.
- Orthogonality Condition: Two non-zero vectors are perpendicular (orthogonal) if and only if their dot product is zero. u⋅v=0⟺u⊥v (for non-zero u and v)
- Dot Product with the Zero Vector: The dot product of any vector with the zero vector is zero. u⋅0=0
These properties make the dot product a fundamental tool in various areas of mathematics, physics, and engineering, particularly for calculating angles, projections, and work done by forces.
Vector Cross Product
- The cross product is defined only in three-dimensional Euclidean space. (each vector can only have three components)
- Unlike the dot product, the result of a cross product is another vector, not a scalar and it is orthogonal to the the multiplicand vectors
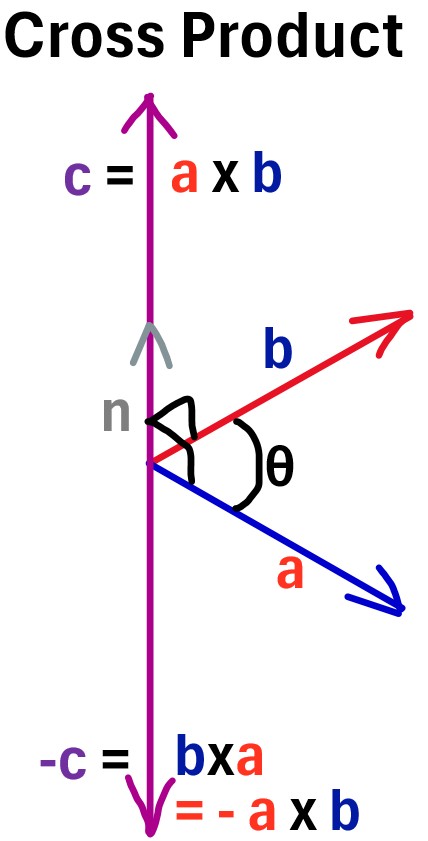
It is denoted as a×b.
The cross product a×b is a vector c that possesses the following characteristics:
Direction: The vector c is orthogonal to both a and b (if the vectors are non zero vectors we can say perpendicular)
Picture: 3 D Coordinates of a Cross Product (order of first and second vectors are unique)
Geometrically the cross product of vectors a and b is a measure of how orthogonal (perpendicular for non zero vectors) a and b are to each other.
- The cross product magnitude is a maximum when the angle between the vectors is 90 degrees.
- The cross product is a vector whose direction will be orthogonal to both vectors a and b\
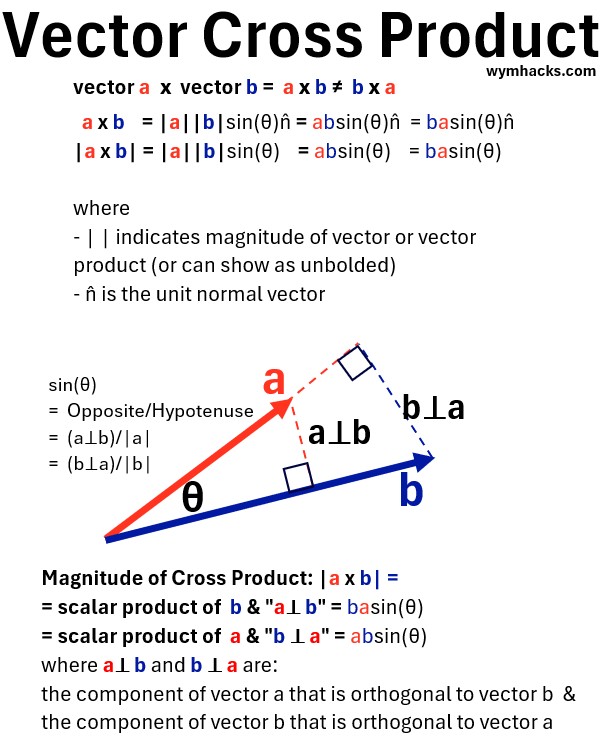
The magnitude of c = a x b is given by the formula: |c|= |axb| =|a||b|sin(θ) where θ is the angle between a and b (0≤θ≤π).
- Vector Form: a x b = |a||b|sin(θ)n = absin(θ)n = basin(θ)n
- Scalar Form: |a x b| = |a||b|sin(θ) = absin(θ) = basin(θ)
- where
- | | indicates magnitude of vector or vector product (or the scalar form is sometimes just un-bolded)
- n is the unit normal vector
- Geometrically, this magnitude represents the area of the parallelogram formed by vectors a and b when their tails are at the same point.
Picture: Geometric Interpretation of Cross Product
- a x b does not equal b x a
- The direction of the cross product is determined by the right-hand rule
- If you curl the fingers of your right hand from the direction of a to the direction of b (through the smaller angle between them), your thumb will point in the direction of c.
- There are actually two other right hand rule methods you can use. I show schematics for all three methods below.
Method 1: Right Hand: Put open hand on plane of vector a, then curl fingers towards b, thumb points in direction of c.
Picture: Vector Cross Product Right Hand Rule Method 1 (Curl)
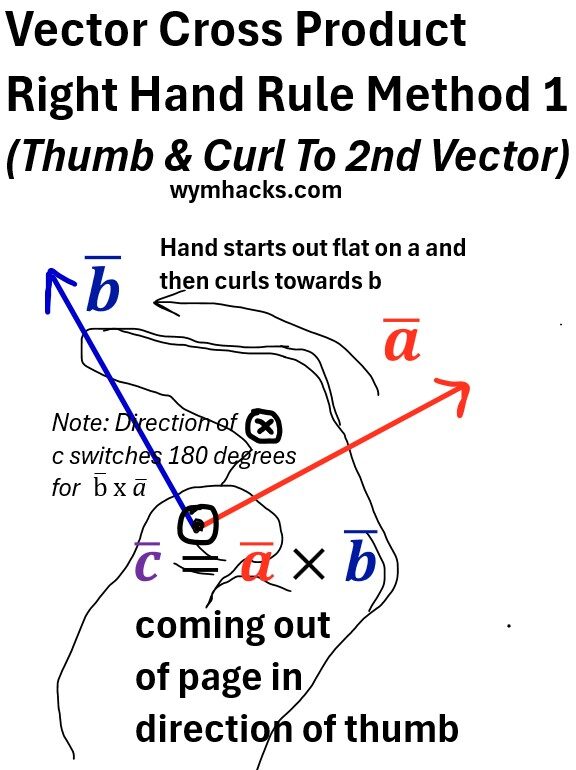
Method 2: Right Hand: Index towards a, Middle finger towards b, thumb points in direction of c
Picture: Vector Cross Product Right Hand Rule Method 2 (Index, Middle, Thumb)
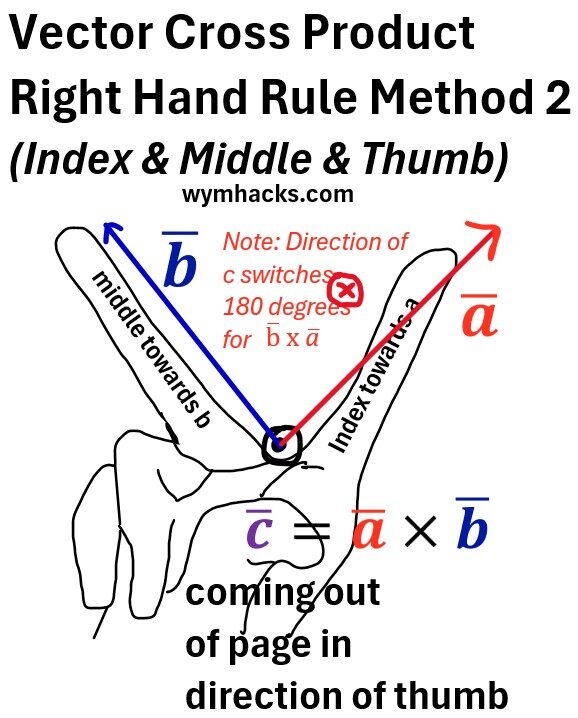
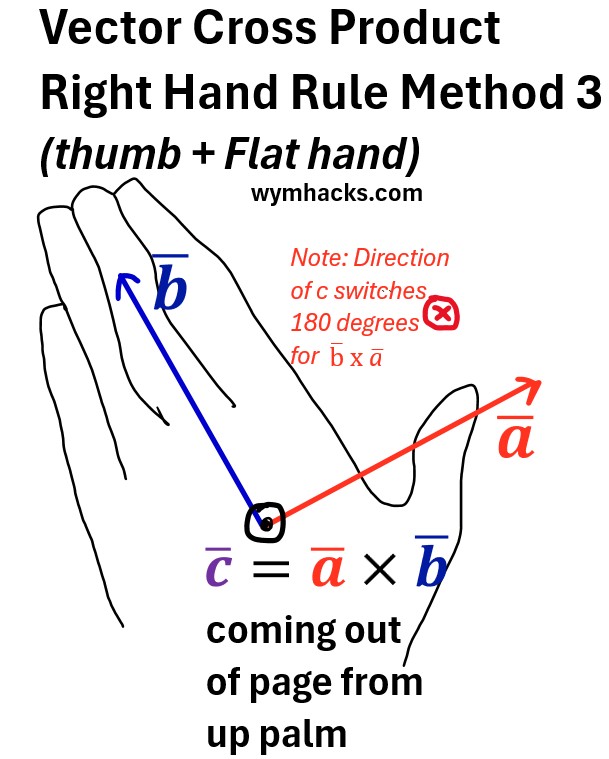
Method 3: Right Hand. Open hand. Thumb towards a and other fingers toward b. Then c comes out of open side of palm.
Picture: Vector Cross Product Right Hand Rule Method 3 (Open Palm)
Algebraic Definition (in Cartesian Coordinates)
Let a = three dimensional vector a and
let b = three dimensional vector b
a = (ax, ay, az)
b = (bx, by, bz)
c = a x b = a vector with three components that are computed as the determinants of three 2 x 2 matrices:
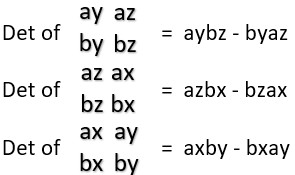
If you look at the a and b vectors as a collection of three columns of components: col1= ax/bx, col2 = ay/by and col3 = az/bz,
notice that the sequence of matrices to compute the determinant on are col2 with col3, then col3 with col1, then col 1 with col2 (a left to right sequence).
So,
c = a x b = (aybz – byaz, azbx – bzax, axby – bxay)
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.