Menu (linked Index)
Circuit Analysis Math Basics: Trig, Complex Numbers, and Euler’s Equation
Last Update: November 19, 2025
Introduction
This article explores the basic math that underpins the modeling of alternating current (AC) circuits.
We begin with the basic geometric ratios of right-triangle trigonometry and extend these concepts using the unit circle to define trigonometric functions for all angles.
We then introduce complex numbers and the geometric rotation property of the imaginary unit j to reveal a powerful mathematical tool: Euler’s formula.
This formula allows us to represent time-varying sinusoidal waveforms (like current and voltage) as simple rotating vectors on the complex plane, providing the essential framework used by engineers to analyze and solve complex electrical systems.
Source:
I heavily used these excellent videos by Willy McAllister
Khan Academy – Electrical engineering Unit 2 Lesson 5 AC circuit analysis
Right Triangle Trigonometry
In a right triangle, you can remember the formulas for sine, cosine, and tangent by using the mnemonic SohCahToa.
Picture: Right Triangle Trig
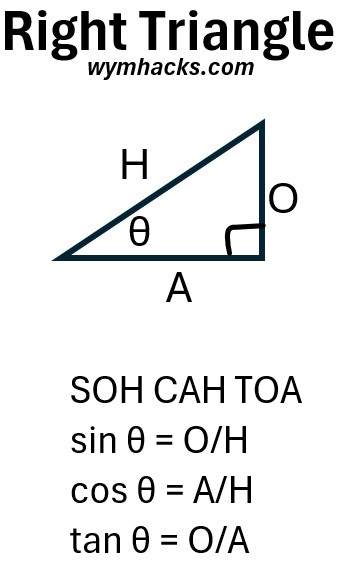
SOH CAH TOA
sin θ = O/H
cos θ = A/H
tan θ = O/A
Unit Circle
The unit circle is a circle with a radius of 1 centered at the origin (0, 0).
It is essential because it is the standard reference used to define the trigonometric functions for any angle θ.
Angles are measured counter-clockwise from the positive x-axis in degrees (0o – 360o ) or radians (0 to 2π).
This framework is crucial for understanding fundamental relationships like the Pythagorean Identity (sin2(θ) + cos2(θ) = 1) and visualizing function periodicity.
Picture: Unit Circle

A Radius of One (Unit)
Since the hypotenuse of any right triangle drawn inside the circle (with one side on the x-axis) is always the radius, and the radius is 1, the trigonometric ratios become incredibly simple:
sin(θ) = opposite}/hypotenuse = 1/y = y
cos(θ) = adjacent/hypotenuse = 1/x = x
This means that for any point (x, y) on the unit circle, the x-coordinate is the cosine of the angle, and the y-coordinate is the sine of the angle.
Extending Trigonometry Beyond 90o
Traditionally, sine and cosine are defined using right triangles, which only works for angles between 0 and 90 degrees.
The unit circle removes this limitation.
By using the coordinate point (x, y) as the definition for (cosθ, sinθ), we can find the sine and cosine for angles in all four quadrants, for angles greater than 360o (by wrapping around the circle), and even for negative angles.
It clearly shows which functions are positive or negative in each quadrant.
- Quadrant I is the area bounded by the positive x and y axis
- Quadrant II, III, and IV follow in a counterclockwise direction
For example, in the second quadrant, x-values (cosine) are negative, but y-values (sine) are positive.
Connecting to Periodic Functions
The unit circle is the foundation for understanding periodic functions like the sine wave and cosine wave.
As an angle increases, the x and y coordinates go up and down in a repetitive, smooth cycle.
This visual movement around the circle is what creates the shape of a wave.
This is crucial for modeling real-world phenomena that repeat, such as voltage, current, light waves, sound waves, or simple harmonic motion.
In short, the unit circle is a convenient, visual, and fundamental tool that makes working with angles and trigonometry much more consistent and powerful.
SOA CAH TOA
sin θ = o/r = y0/r
cos θ = a/r = xa/r
tan θ = o/a = y0/xa = rise/run = slope
Unit Circle
r = 1
θ Measured Counter-Clockwise from positive x axis
θ in degrees or radians (0o – 360o) or (0 – 2π radians)
1 radian = 57.3o where arc = radius
Complex Numbers
This section is a high level review of complex numbers.
Refer to my blogs
for more information.
Complex numbers are extensions of real numbers, formed by combining a real part and an imaginary part.
The imaginary part is based on the imaginary unit i (or j in electrical engineering) , which is defined as the square root of negative one √-1.
In electrical engineering they can be written in the form z = x + jy, where x and y are real numbers.
They are essential for solving equations that have no real solutions (i.e. finding roots of finding the roots of all polynomial equation.
Complex numbers are essential in electrical engineering because they provide a powerful, simplified way to analyze Alternating Current (AC) circuits.
They allow engineers to treat the two defining characteristics of AC signals—magnitude (size) and phase (timing shift)—as a single algebraic quantity, vastly simplifying calculations.
Picture: Complex Plane: Imaginary Number
Complex Numbers
- based on imaginary number or unit j
- j known generally as “i” but in Electrical Engineering “j” is used to avoid confusing it with current
- j2 = -1
- Most agree they are badly named (not really imaginary)
- Very useful in Electrical Engineering (e.g. AC circuit analysis)
- complex number: z = x + jy
- z = complex number
- x = real part and
- y = real also but is called the imaginary part
- jy = imaginary term
- I see this being called the imaginary part as well but to avoid confusion we’ll stick to imaginary term.
- Real numbers are a subset of the Complex numbers (e.g. z = x + 0 = x is a real number)
- plot in the complex plane;
- real part on x axis and
- imaginary part on vertical axis
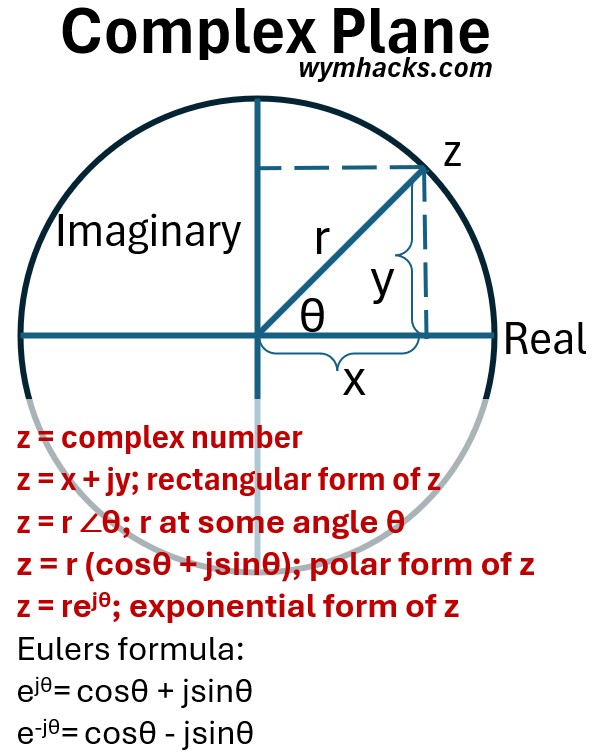
Two common ways to express a complex number are:
z = x + jy ; complex number equation in rectangular form
- x = real part and
- y = (real) imaginary part
- jy = imaginary term
z = r ∠θ ; complex number z
- reads as “r at some angle θ”
From the unit circle we know that:
- x = rcosθ
- y = rsinθ
- r2 = x2 + y2
- tan θ = y/x
- θ = arctan (y/z)
Substituting x = rcosθ and y = rsinθ into “z = x + jy” gives a 3rd way of expressing complex numbers:
z = r (cosθ + jsinθ); polar form of z
Euler’s Formula
If you are interested in more details around Euler’s Formula you can start with my post: Exploring Euler’s Formula.
Here I’ll just present two forms of the equation:
ejθ = cosθ + jsinθ; Euler’s Formula
e-jθ = cosθ – jsinθ; Euler’s Formula
We can use the first Euler’s Equation above to express a complex number in a fourth way:
z = rejθ ; exponential form of z
Powers of Imaginary Unit j
Complex numbers can be displayed visually on a complex plane.
The complex plane is a two-dimensional coordinate system used to graph complex numbers.
Unlike the standard Cartesian plane with an x and y axis, the complex plane has
- a real axis (the horizontal axis, representing the real part) and
- an imaginary axis (the vertical axis, representing the imaginary part).
Any complex number z = x + jy is plotted as a single point with coordinates (x, y), giving it a visual location that is crucial for understanding operations like addition and multiplication geometrically.
Multiply j by Itself
Lets plot the consecutive multiples of j on the complex plane.
- j0 = 1
- j1 = j
- j2 = -1
- j3 = -j
- j4 = 1
- j5 = j
- j6 = -1
- j7 = -j
- j8 = 1
- etc…
Picture: Complex Plane: Imaginary Number
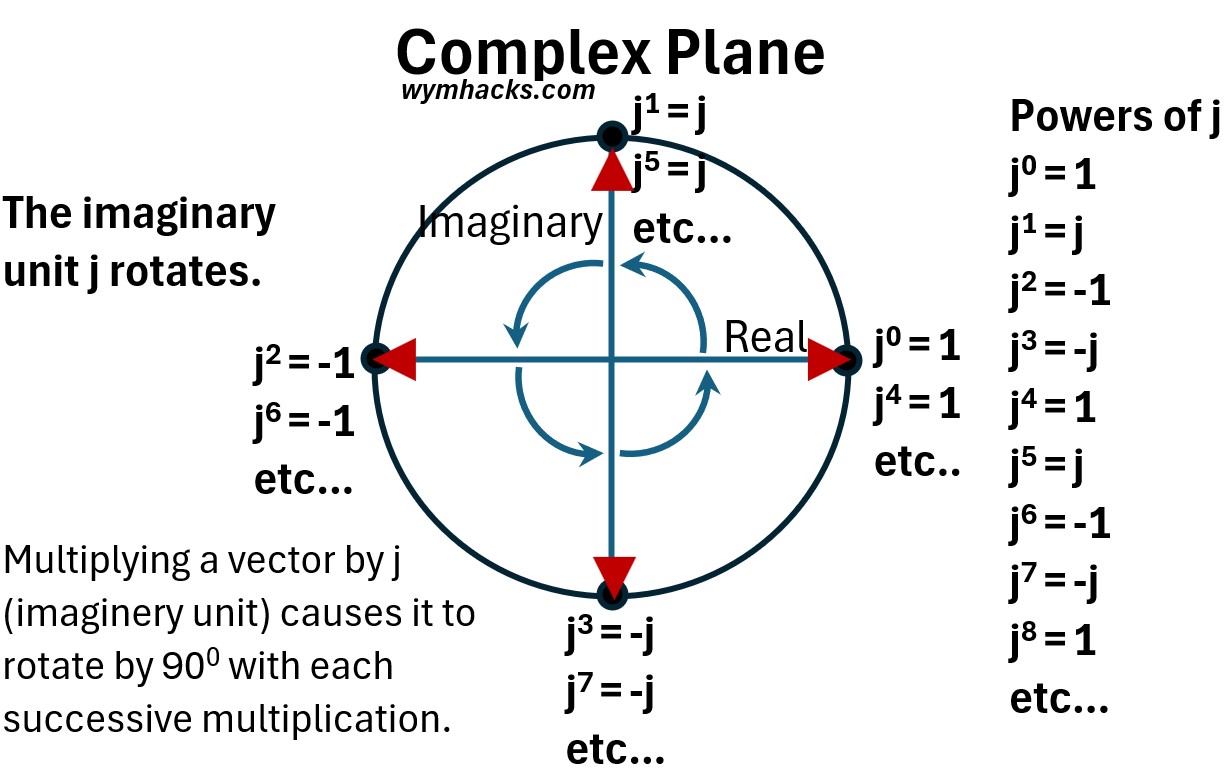
Plotting these power of j onto the complex plane results in a repeating circular pattern.
- eg. j0 = j4 and j1 = j5 etc.
- The j “to the power” values result in a repeating 1, j, -1, -j sequence
We see that
Multiplying a vector by j (imaginary unit) causes it to rotate by 900 with each successive multiplication.
The imaginary unit j rotates.
An interesting Property of j
j-1 = 1/j
multiply the right hand side by j/j
(1/j)(j/j) = j/j2
since j2 = -1 we get
j-1 = -j
j Multiplier Rotates z by +900
The act of multiplying any complex number z by the imaginary unit j performs a counter-clockwise rotation of 900 (or π/2 radians) around the origin on the complex plane.
Multiplying A Complex Number by j (Rectangular Form)
Starting with a complex number z which we will arbitrarily place in the 1st quadrant of the complex plane (I).
z = a + jb
multiply by j
jz = ja + jjb
jj = j2 = -1 , so
jz = -b + ja
From the picture below,
- the z vector (from circle center to point z on the circumference of circle in a complex plane) is plotted in the first quadrant (I).
- the resultant jz vector is located in the second quadrant (II)
Picture: Complex Plane: Multiplying by j
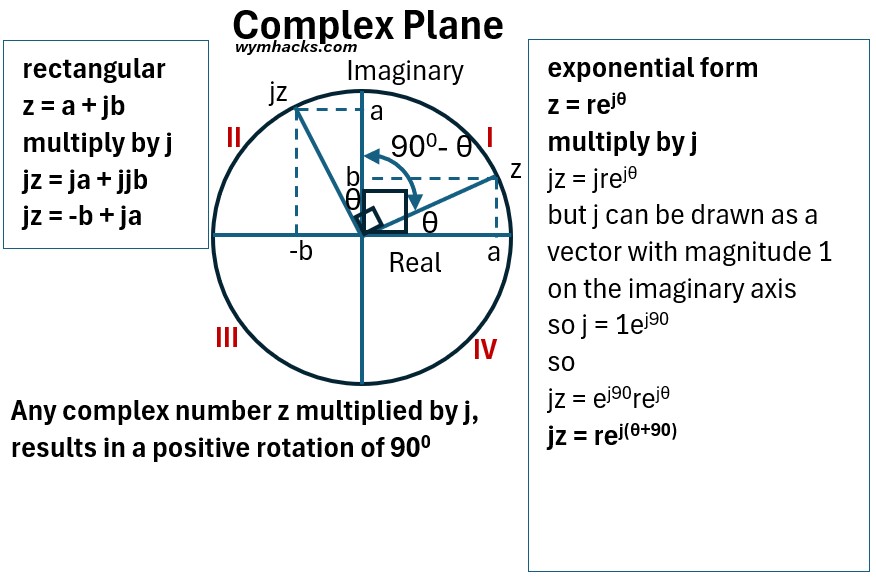
We can prove that the vector result is a 900 degree positive (counterclockwise) shift in the complex plane
Proof that Angle between z and jz is 900
Refer to the picture as you read the simple proof below:
- z moved by 900 to jz
- We know that the angle of the vertical and horizontal axis in quadrant I is 900 (represented by the larger angle “box”), so
- θ + (900– θ) = 900
- So jz must be at 900 from z (represented by the smaller angle “box”)
We can do the same multiplication using the exponential form of a complex number.
Multiplying a Complex Number by j (Exponential Form)
z = rejθ
multiply by j
jz = jrejθ
but j can be drawn as a vector with magnitude 1 on the imaginary axis
so j = 1ej90
then
jz = ej90rejθ
so,
jz = rej(θ+90)
Therefore,
Any complex number z multiplied by j, results in a positive rotation of 900
Cosine and Sine Expressions from Euler’s Formula
Euler’s Formula(s)
ejθ = cosθ + jsinθ; Euler’s Formula
e-jθ = cosθ – jsinθ; Euler’s Formula
Check out my blog Exploring Euler’s Formula to learn about this amazing equation.
Electrical engineers love Euler’s formula for two reasons:
- Euler’s relates exponentials to cosine and sine
- e is easily to deal with mathematically
- d/dx (ex) = ex ; the derivative of ex is itself
- d/dx (eax) = aeax ; the derivative of eax is a scalar of itself
- Sinusoids (sines and cosines) happen in nature
- e.g. music and sound travel in pressure waves
- e.g. circuits make sine waves
- etc.
Add Euler’s Equations
Add the two Euler’s equations below
ejθ = cosθ + jsinθ; Euler’s Formula
e-jθ = cosθ – jsinθ; Euler’s Formula
To get,
ejθ + e-jθ = 2 cosθ
Rearranging, we get an expression for cosθ:
cosθ = 1/2 (ejθ + e-jθ) ; cosine definition in terms of exponentials
Subtract Euler’s Equations
Subtract the two Euler’s equations below
ejθ = cosθ + jsinθ; Euler’s Formula
e-jθ = cosθ – jsinθ; Euler’s Formula
to get,
ejθ – e-jθ = 2jsinθ
Rearranging, we get an expression for sinθ:
sinθ = (1/2)(1/j)(ejθ – e-jθ) ; sine definition in terms of exponentials
Preference In Electrical Engineering to use Cosine
In electrical engineering, the cosine function is the preferred method for representing AC voltage and current sinusoids,
- A cos(ω t + Φ), because
- it maps directly to the real part of the complex number used in phasor analysis.
Using Euler’s formula, ejθ = cosθ + jsinθ,
- taking the real part of the complex exponential
- simplifies the time-domain differential equations into algebraic equations,
- allowing the amplitude and phase information to be easily tracked and manipulated for circuit analysis.
ejθ Spins
Let’s plot Euler’s formula in the complex plane
ejθ = cosθ + jsinθ; Euler’s Formula
Picture: Complex Plane: ejwt Spins

The magnitude (by definition) of ejθ is:
|ejθ| = sqrt{ (real part)2 + (imaginary part)2 }
so,
|ejθ|2 = cos2θ + sin2θ = 1
therefore,
|ejθ| = 1
So ejθ is somewhere on circumference of this circle at an angle θ.
As the angle changes, ejθ spins (rotates) in a circular path.
For something not on the unit circle we have
Aejθ ,
where A is some amplitude and where
|Aejθ| = A (i.e. a circle with radius A)
Picture: Complex Plane: ejθ Spins

We can express the angle θ (units of radians) as angular velocity x time = ωt (rad/s x s = radians).
So we can also say that ejωt spins (rotates) in a circular path.
ejωt Spins
Recall our cosine expression in terms of exponentials
cosθ = 1/2 (ejθ + e-jθ) ; cosine definition in terms of exponentials
let x = ωt where
- ω = angular velocity (rad/s)
- t = time in s
Substitute into the cosine equation above
cos(ωt) = 1/2 (ejwt + e-jwt)
- ejwt is a complex number;
- It’s magnitude is 1;
- It’s angle increases with t;
- and it completes a full circle at ωt = 2π;
- It is rotating with time.
- e-jwt is a complex number with the same properties but rotates with time in the opposite direction
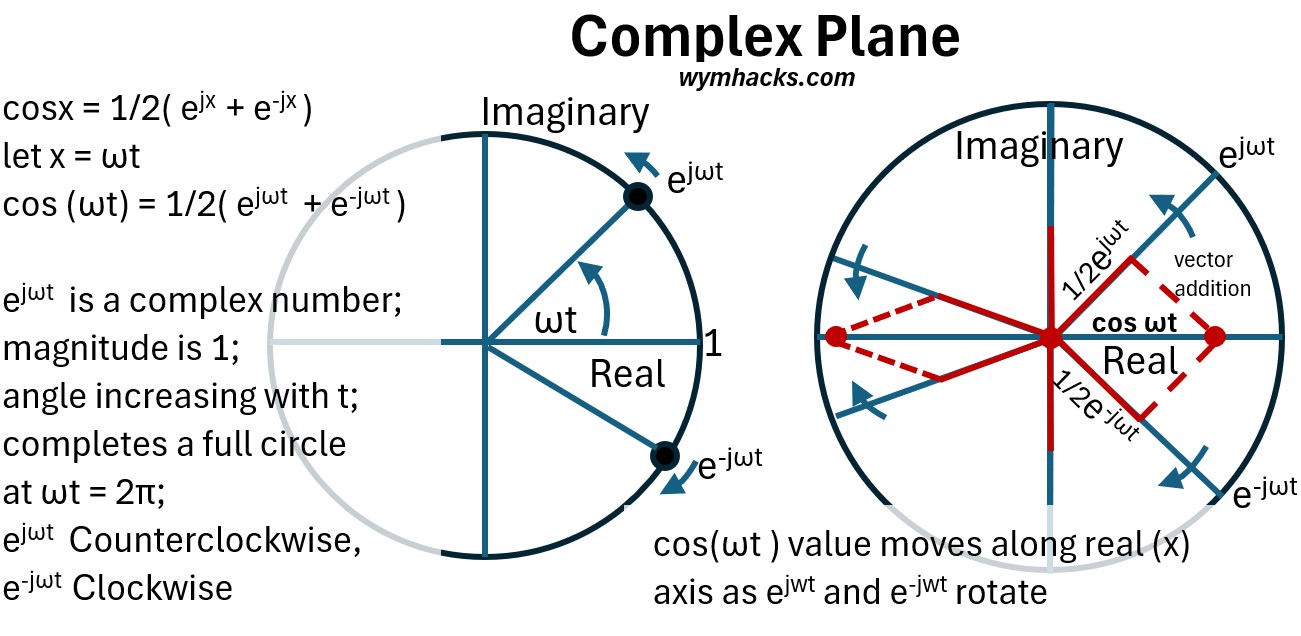
Check out the picture below where
- ejwt rotates counterclockwise,
- e-jwt rotates clockwise
- and the sum of the vectors 1/2 ejwt
- and 1/2 ejwt
- equal the values cos (wt) located on the real axis (the x axis)
Picture: Complex Plane: Cos From Euler’s Equation
If we start with the sine form of the equation:
sin(ωt) = (1/2)(1/j)(ejwt – e–jwt) ; sine definition in terms of exponentials
then we’ll get a similar complex plane chart but now
- the sum of the vectors 1/2 ejwt
- and –1/2 ejwt
- equal the values jsin(ωt) located on the imaginary axis (the y axis)
Very cool!!
We can these equations and the complex plane to project the values of cos(ωt) and sin(ωt) onto a graph over time, resulting in sinusoid curves.
These can be and are used to model voltage and current in AC systems for example.
See these beautiful videos created by Willy McAllister.
https://www.khanacademy.org/ee-ac-analysis/v/ee-eulers-sine-wave
https://www.khanacademy.org//ee-ac-analysis/v/ee-euler-cosine
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.