Capacitance

Capacitance Equation Derivation

In my post,  Electric Field of a Charged Infinite Plane , we established that the magnitude of the electric field E of a uniformly charged infinite plate (plane) is

E = 2(k)(π)(σ) = (σ)/(2εo)

= Magnitude of the electric field (E) at any point outside a single, infinite, uniformly charged plane (plate)

where

• k = 1/(4πε₀) = coulomb’s constant
• ε0 = electric constant = electric permittivity of free space (i.e. a vacuum)
• ε0 = 8.854e-12 C2 / Nm2  or can use units of “F/m” or “s4A2/(m3kg)”

• σ = charge density = Q/A

2 Plates 

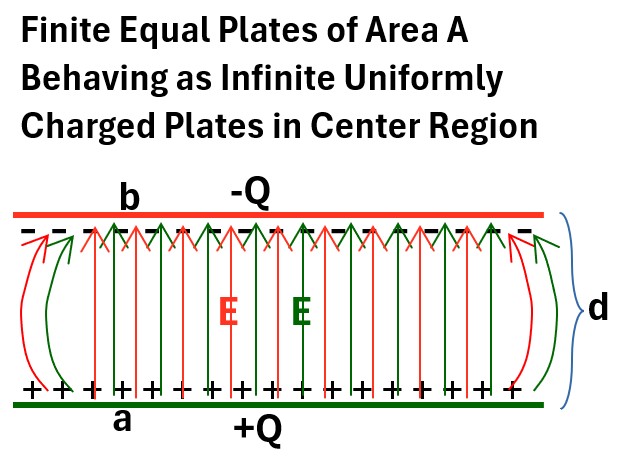
Imagine two uniformly charged but finite plates of equal Area A and separated by a distance d. 

• One plate is positively charged and the other is negatively charged
• Assume that away from the edges, the plates behave like infinite , uniformly charged plates.

So we’ll have something like the picture below. 

Picture: Finite Equal Oppositely Charged Plates 

Each plate will generate an electric field and they will all point towards the negative plate.

Away from the edges we assume we have constant and perpendicular E lines. 

Total Magnitude of E

Each plate will generate an electric field with magnitude 2(k)(π)(σ) so the total electric field of both plates will be:

(1) E = 2(k)(π)(σ) + 2(k)(π)(σ) = 4(k)(π)(σ) = 4(k)(π)(Q/A)

Voltage Across the Plates

Let’s choose two points a and b across from each other on the plates. 

The Voltage between a and b will be the Electric Potential Difference between them. 

And this will be equal to the amount of energy it takes to move 1 Coulomb of positive charge from b to a.

Work = (1 Coulomb)(E Newtons/Coulomb)(d)

So, 

(2) Voltage = Joules/Coulomb = Work/Charge = (E)(d)

Substitute (1) into (2) to get

Voltage = (E)(d) = [4(k)(π)(Q/A)](d)

which can be rearranged to:

(3) Q/V = C = A/(4kπd) ;Parallel Plate Capacitor

where C = Capacitance and has units of Farad.

If we substitute for k = 1/(4πε₀) = coulomb’s constant in equation (3) we get

(4) Q/V = C =  (Aεo)/d ;Parallel Plate Capacitor

Where 

• εo = 1/[4kπ]
• k = 1/(4πε₀) = coulomb’s constant

The equations above apply to two charged plates in a vacuum or air. 

Capacitance

Capacitance is a measure of an object’s ability to store an electric charge.

The higher the capacitance, the more charge it can hold for a given voltage.

• The primary component designed to do this is called a capacitor.

The standard unit for capacitance is the farad (F), named after Michael Faraday.

• Most electronic components are measured in microfarads ($\mu$F) or picofarads (pF).

In its simplest form, a capacitor consists of two conductive plates separated by an insulating material called a dielectric.

A dielectric will do two things

• It keeps the metal separated so no circuit exists and
• it always increases the capacitance (non conducting dielectrics always increase the capacitance).

If C is the capacitance of a capacitor before a dielectric is installed, then the capacitance after a dielectric is installed is κC

• where κ is the dielectric constant of that material.
• κ is a dimensionless quantity that measures a material’s ability to store electrical energy within an electric field.

The capacitance is determined by the physical properties of the capacitor:

• The area of the plates.

• The distance between the plates.

• The type of dielectric material used

For a parallel plate capacitor with a dielectric installed, the equations are:

(5) Q/V = κC = κA/(4kπd); Parallel Plate Capacitor with dielectric

(6) Q/V = κC =  κ(Aεo)/d ; Parallel Plate Capacitor with dielectric

where

• κ = dielectric constant of dielectric material
• C = Capacitance and has units of Farad = F =  C/V
• k = 1/(4πε₀) = coulomb’s constant (Nm²/C)
• ε0 = electric constant = electric permittivity of free space (i.e. a vacuum)  (F/m)
• A = area of one of the plates (m²)
• d = distance between the plates (m)
• Q = charge on one of the plates (C)
• V = voltage across the plates (J/C)

Return to Menu