Menu (linked Index)
Electric Field of a Charged Infinite Plane
Last Update: September 20, 2025
Introduction
The magnitude of the electric field E of a uniformly charged infinite plate (plane) is
Total E = 2(k)(π)(σ) = (σ)/(2εo)
= Magnitude of the electric field (E) at any point outside a single, infinite, uniformly charged, non-conducting plane.
where
- k = 1/(4πε0) = coulomb’s constant
- ε0 = electric constant = electric permittivity of free space (i.e. a vacuum)
- ε0 = 8.854e-12 C2 / Nm2 or can use units of “F/m” or “s4A2/(m3kg)”
- σ = charge density = Q/A
In this post I’ve used Sal Khan’s excellent videos to derive these expressions
Read this post and enjoy a little vector math, trigonometry , and calculus applied to a real-world (although idealized) physics problem.
Computation Set Up
The picture below shows an infinite plate sitting on the xy plane of a cartesian coordinate system.
The plate is represented by the black dotted line.
Picture: Test Charge in an Infinite Uniformly Charged Plate
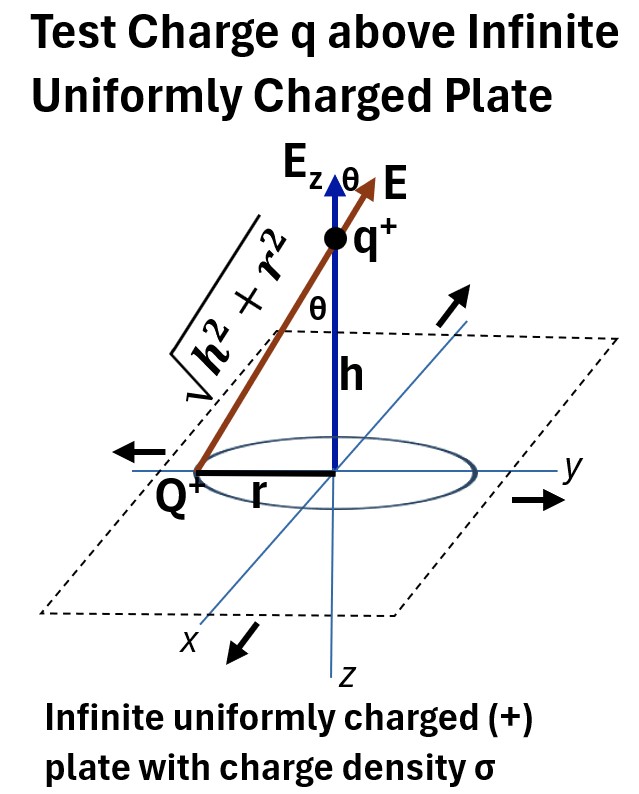
Let’s assume
- the plate is positively and uniformly charged.
- the charge density of the plate is σ which is the Charge (Q) per unit Area (A): Q/A
- a positive test charge q is placed a height h above the plate.
Now, choose a point charge on the plate that is on the circumference of a circle with radius r.
Pythagoras tells us that the distance from this point on the plate to q will be √(h2 + r2)
Symmetry in the Infinite Uniformly Charged Plate
The arbitrary point on the plate that we chose will put an electric force F and an electric field E at q.
- these are both vectors that point outwards (because the plate and the charge are positive).
- the E vector is the brown arrow in the picture above.
We want to compute the magnitude of the electric field at the test charge.
In a uniformly charged infinite plate the E to compute at q will be the vertical component shown as Ez in the picture above.
This is due to symmetry and the cancellation of the non vertical E field vector components, i.e.
- for every Q on the plate there will be an opposite Q on the hypothetical circle we are in (on the plate).
- These two E vectors (which can be broken down into vertical and horizontal components) will sum to a vertical vector only because the horizontal vectors cancel out.
- See Appendix 1 for a nice drawing and a more detailed description.
Equation Development
Let’s put the same picture below as we set up our equation.
Picture: Test Charge in an Infinite Uniformly Charged Plate

We want to compute Ez, the magnitude of the electric field at the test charge q.
(1) Ez = Ecosθ; where cosθ = Adjacent/Hypotenuse in a right triangle
The Vertical Angle Theorem says that when two lines intersect, the angles that are directly opposite each other are called vertical angles, and they are always equal.
So the vertically located acute angle of the “big triangle” also has this same angle θ.
So, we can re-write (1) using the sides of the bigger triangle.
(2) Ez = Ecosθ = (E)(Adj/Hyp) = (E)(h)/√(h2 + r2)
Now, consider the point charge Q+ that sits on the circumference of this hypothetical circle we imagined on the plate.
Assume this circumference has an infinitesimally small width of dr such that we can define the area of this ring as:
ring area = circumference x width = (2πr)(dr)
We know the charge density so we can compute the total charge of this singular ring:
(3) Qr = (Area of ring)(charge density) = (2πr)(dr)(σ)
Determine the electric field generated by this ring.
Coulomb’s law (see Appendix 2) for the Force generated by the ring will be
(4) Fr = (k)(Qr)(q)/(d2) = (k)(Qr)(q)/(√(h2 + r2))2 = (k)(Qr)(q)/(h2 + r2)
Since E = F/q we can re-write (4) in terms of Er
(5) Er = (k)(Qr)/(h2 + r2)
Substitute (5) into (2):
(6) Erz = (Er)(h)/√(h2 + r2) = ( (k)(Qr)/(h2 + r2) )* (h)/√(h2 + r2)
Substitute (3) into (6) and clean it up a little to get
(7) Erz = (k)(h)(2πr)(dr)(σ)/(h2 + r2)3/2
Equation (7) is the magnitude of the E field at q for 1 infinitesimal ring on the infinite plate.
We need to integrate this so we can sum up the E values for the entire plate.
Integration
We want to integrate equation (8) and move the constants out of the integral,
- except we’ll keep the constant 2 inside the integral so we can solve by parameterization.
(8) ∫r = 0 to ∞Erz =(k)(h)(π)(σ)∫r = 0 to ∞(2r)(dr)/(h2 + r2)3/2
Let
(9) u = h2 + r2
then
(10) du/dr = 2r
and
(11) du = 2rdr
Substitute (9) and (11) into the (8)
(12) ∫r = 0 to ∞Erz = (k)(h)(π)(σ)∫r = 0 to ∞du/(u)3/2
(13) ∫r = 0 to ∞Erz = (k)(h)(π)(σ)∫r = 0 to ∞(u)-3/2du
(14) ∫r = 0 to ∞Erz = (k)(h)(π)(σ)[-2/√u]r = 0 to ∞
Substitute for u using (9)
(15) ∫r = 0 to ∞Erz = (k)(h)(π)(σ)[-2/√(h2 + r2)]r = 0 to ∞
(16) ∫r = 0 to ∞Erz = (k)(h)(π)(σ)-2[0 – 1/√(h2 )]
(17) ∫r = 0 to ∞Erz = 2(k)(h)(π)(σ)/(h)
The h terms cancel out! This means the magnitude of the electric field is independent of the distance from the plane.
(18) ∫r = 0 to ∞Erz = Total E = 2(k)(π)(σ) ; Magnitude electric field (E) at any point outside a single, infinite, uniformly charged, non-conducting plate.
For this formula to hold true, several key conditions must be met:
- Non-conducting Plane: The formula is for an insulating or non-conducting plane.
- This ensures that the charge is distributed uniformly and remains fixed on the surface.
- Infinite: The plane must be considered infinite in size.
- The electric field lines are therefore perfectly parallel and perpendicular to the surface.
- The field from charges far away perfectly cancels out all parallel components, leaving only the perpendicular component.
- This also means that the magnitude of the electric field is independent of the distance from the plane.
- Uniformly Charged: The charge must be spread uniformly across the surface,
- meaning the surface charge density (σ) is constant everywhere.
- Test Charge Location: The formula gives the field magnitude at a test charge q, but
- the value of E does not depend on the test charge itself.
- The test charge is simply used to measure the field.
Expressed in Terms of Electric Permittivity
Total E = 2(k)(π)(σ) ; Magnitude electric field (E) at any point outside a single, infinite, uniformly charged, non-conducting plate.
We know that (see Appendix 2)
- k = 1/(4πε0) = coulomb’s constant
- ε0 = electric constant = electric permittivity of free space (i.e. a vacuum)
- ε0 = 8.854e-12 C2 / Nm2 or can use units of “F/m” or “s4A2/(m3kg)”
Total E = 2(1/(4πεo))(π)(σ) = (σ)/(2εo) ; Magnitude electric field (E) at any point outside a single, infinite, uniformly charged, non-conducting plate.
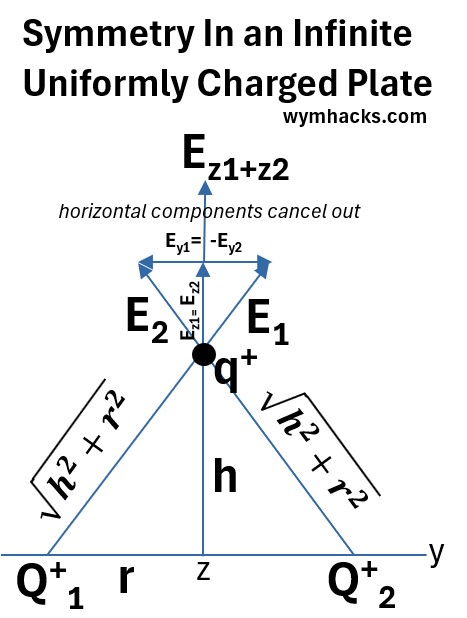
Appendix 1: Symmetry in a Uniformly Charged Plane
On an infinite uniformly charged plane; if we pick a radius of points and then pick two opposite points, the E vectors at a test charge will point in different directions but have the same magnitude.
If you add these vectors up, the result is the sum of the vertical components because the horizontal components cancel out.
i.e. The geometric addition of the electric field vectors from two symmetrically opposite points on a uniformly charged plate results in a vector that points only vertically (perpendicular to the plate).
In the picture below, a side view of the plate is shown on a y axis.
Picture: Symmetry in an Infinite Uniformly Charged Plate
Individual E-Field Vectors
Every tiny piece of charge on the plate creates its own electric field.
For two symmetrically opposite points on a radius, their individual electric fields at a test charge will have the same magnitude because they are the same distance away.
However, they will point in different directions, forming a symmetrical “V” shape.
Vector Decomposition
Each of these two vectors can be broken down into two components:
A vertical component (Ez) that points perpendicular to the plate.
A horizontal component (Ey) that points parallel to the plate.
Cancellation of Horizontal Components
Because the two original points are symmetrically opposite, their horizontal components will be equal in magnitude but point in opposite directions.
When you add these two vectors, the horizontal components cancel each other out completely (Ey +(−Ey)) = 0.
Summation of Vertical Components
The vertical components, however, both point in the same direction (straight up because all charges are positive).
Therefore, they add together.
The total electric field from these two points is the sum of their vertical components.
This principle of vector cancellation due to symmetry is the reason why the electric field of an infinite uniformly charged plate is a simple, uniform field that is always perpendicular to the plate.
Appendix 2: Coulomb’s Law
The magnitude or strength of the electric force between two charged particles is given by:
Fe = kq1q2/r2 ; Magnitude of Electric (Electrostatic) Force
- Fe = electrostatic force
- q1, q2 =The quantity of charge of objects 1 and 2
- F is positive when q1 and q2 are of like charge and negative when q1 and q2 are of opposite charge.
- r = distance between the charges.
- Notice the inverse square relationship between force and distance.
- k = 1/(4πε0) = coulomb’s constant
- ε0 = electric constant = electric permittivity of free space (i.e. a vacuum)
- ε0 = 8.854e-12 C2 / Nm2 or can use units of “F/m” or “s4A2/(m3kg)”
- k = 8.99e9 Nm2/C2
- F = farad
- 1 F = 1 s4A2/(m2kg) where
- A = ampere
- 1 A = 1 C/s
- m = meters
- kg = kilograms
In general Permittivity ε indicates how much a material resists the formation of an electric field within it.
- A material with high permittivity will oppose the formation of an electric field more strongly
- than a material with low permittivity.
ε0 is a measure of how dense of an electric field is “permitted” to form in response to electric charges (in a vacuum).
- ε0 is a measure of how “permissive” the vacuum of space is to the formation of an electric field (which are generated by electric charges).
- ε0 tells you the relationship between the amount of charge and the strength of the electric field it creates in empty space.
Check out these videos:
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.