Menu (linked Index)
Faraday’s Law and Lenz’s Law
Last Update: Sept 26, 2025
Introduction
Michael Faraday discovered that a changing magnetic field could induce a current.
His breakthrough came in 1831 with a series of ingenious experiments. (see my post: Faraday’s 1831 Electromagnetic Experiments)
In one of the experiments, he wrapped two coils of wire around an iron ring, and observed a brief, momentary current in the second coil only when the current in the first was starting or stopping.
This showed that a changing magnetic field could induce a current.
He further demonstrated this by moving a bar magnet into and out of a coil of wire, noting that a current was only produced when the magnet was in motion.
He also built the first electric generator, the Faraday disc, which used a rotating copper disc to produce a continuous direct current.
In this post we’ll explore Faraday’s law of induction, which mathematically describes how a changing magnetic field creates an electromotive force (or voltage).
We will then introduce Lenz’s law, which provides a crucial addition to Faraday’s law by explaining the direction of the induced current and the opposition to the change that created it.
These concepts are fundamental because they explain the principle of electromagnetic induction, which is the basis for how electric generators, transformers, and many other electrical devices operate.
Consider reading this book if you want to learn about Michael Faraday and James Clerk Maxwell, the man who codified his experimental discoveries.
- Faraday, Maxwell, and the Electromagnetic Field by Nancy Forbes and Basic Mahon; 2019 by Prometheus Books
Magnetic Flux
Let’s start with the definition of magnetic flux.
Picture: Magnetic Field B and Magnetic Flux

Magnetic flux , ΦB , is the measure of a magnetic field passing through a surface.
ΦB = Magnetic Flux = (B)(Ap) =BAcos(θ) = B̄•Ā ; for Uniform B and Flat Surface where
- ΦB = magnetic Flux (units: (N/C)m2)
- Ap (units: m2) = Perpendicular component of A that the magnetic field passes through.
- B = The magnetic field (units: N/C)
- B̄•Ā = dot product of the magnetic field vector and the area vector.
- θ = angle between area vector and B vector
ΦB = Magnetic Flux =∫BdAcos(θ) =∫sB̄•dĀ for any B for any surface
- For any B through any surface we can restate the equation as the surface integral ∫s of B times infinitesimal areas.
- This is a a general expression for the magnetic flux through any surface
So, what can change magnetic flux? From the equation (and the drawing) we know it is
- A change in the magnitude of B
- A change in the surface area B passes through and
- A change in the angle between B and the surface
Faraday’s Law of Electromagnetic Induction (The Flux Rule)
It was the Scottish physicist James Clerk Maxwell, about 30 years later, who translated Faraday’s experimental work and conceptual ideas into the precise mathematical form we use today.
The general form of Faraday’s law of induction describes how a changing magnetic field creates an electromotive force (EMF) in a circuit (i.e. electromagnetic induction):
EMF=−NdΦB/dt ; Faraday’s Law of Electromagnetic Induction (the Flux Rule)
or
EMFavg=−NΔΦB/Δt ; Faraday’s Law of Electromagnetic Induction (the Flux Rule) – Average form
where
- EMF (symbolized as ε) is the induced electromotive force (EMF).
- EMF is not really a force.
- It is a measure of the energy per unit charge, similar to voltage, that causes a current to flow in a closed circuit.
- It’s measured in Volts (V).
- The EMF is the driving potential that gets charges moving.
- N: the number of turns in the coil of wire.
- is the sum of the EMFs induced in each individual loop.
- dΦB/dt : the instantaneous rate of change of the magnetic flux through the circuit.
- ΦB : the magnetic flux
- The Negative Sign (-): this represents Lenz’s Law (more on this below).
- i.e. the direction of the induced EMF (and the resulting current) is such that it creates a magnetic field that opposes the change in magnetic flux that produced it.
- The average form of Faraday’s law of induction is used to calculate the average induced electromotive force (EMF) over a specific, finite time interval.
- You write it by replacing the differential symbols with delta symbols.
Faraday’s Law: Coil in a Magnetic Field
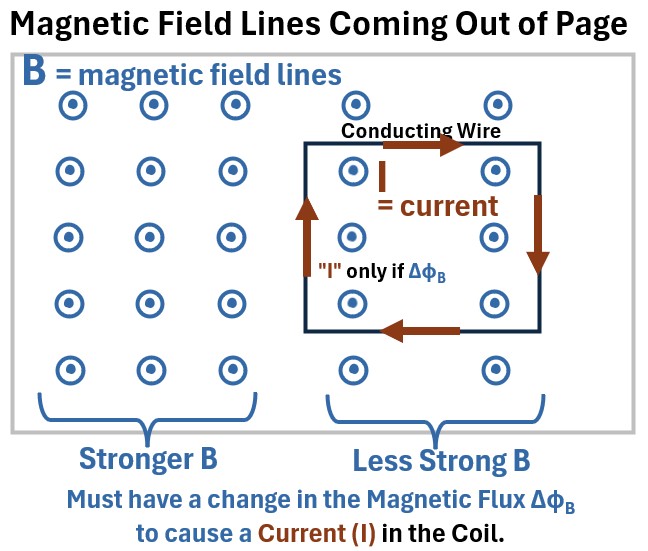
The picture below is a plan view of a magnetic field coming out of the page towards you (represented by the circles with dots…where you can imagine the dots to be the tips of arrows).
We’ll drop a rectangular conducting coil into this field such that its bounded surface is perpendicular to the B field.
Picture: Magnetic Field Lines With Closed Loop Conducting Wire
The B field is shown as having various fixed (constant) intensities based on the distance of the points from each other.
As long as the field is constant and the coil is stationary we will not see any current in this coil.
A current “flows” in the wire only if the magnetic flux changes.
So, a current I will start “flowing” in the loop if the magnetic flux changes somehow (ΔΦB > 0):
- e.g. the flux strength decreases or increase
- e.g. the conducting wire boundaries are expanded or contracted
The current I direction is shown going clockwise in the schematic. How do we know that? Read on!
References
Lenz’s Law
Induction and Lenz’s Law (The Negative Sign In Faraday’s Law)
Lets rotate the picture in the previous section so we see a side view of the coil and the magnetic field lines coming up through it (see below).
Now, let’s increase the strength of the magnetic field lines and show these as bigger vectors in the “after the arrow” drawing below (ΦB1 → ΦB2).
Picture: Changing Magnetic Field Lines through a Closed Conducting Wire
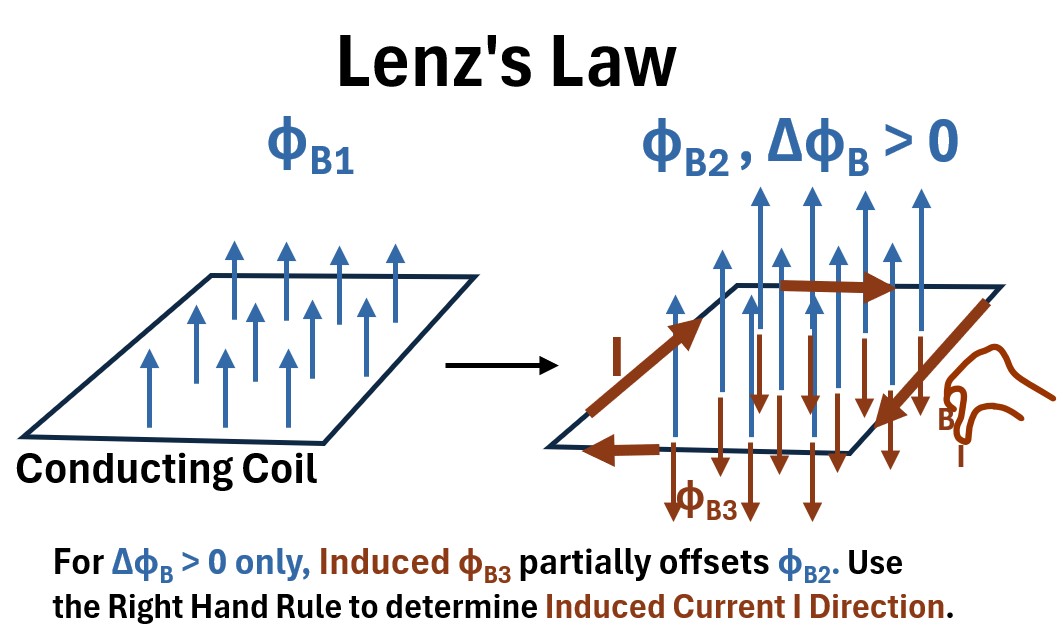
This is what happens:
(1) Change ΦB1 by amount ΔΦB which
(2) induces an Electric Field which
(3) induces a Voltage which
(4) induces Current I which
(5) induces an oppositely directed ΦB3 which
(6) partially offsets ΦB2 .
(7) Based on ΦB3 ‘s direction, use the Right Hand Rule to determine I direction (clockwise in this example).
Lenz’s Law states that the direction of an induced current is such that it creates a magnetic field that opposes the change in magnetic flux that created it.
- This is conservation of energy in action.
- It ensures that to induce a current, you must do mechanical work against a resulting opposing force.
- If the induced current did not oppose the change, it would create a self-perpetuating loop of increasing current and energy from nothing.
Lenz’s law simply states that nature abhors a change in magnetic flux.
- The induced current will always produce a magnetic field that opposes the change that caused it.
- This opposition is why the induced EMF in Faraday’s law has a negative sign
References
This section is mostly based on this great video by Sal Khan.
EMF Expression For a Closed Conducting Loop
So, we have a general expression for Faraday’s law and understand the negative sign through Lenz’s law:
EMF=−NdΦB/dt ; Faraday’s Law of Electromagnetic Induction (the Flux Rule)
Now, we want to develop an expression for the EMF and use it to explain interactions of a magnetic field and a conducting coil.
EMF
We see that the induced voltage, or electromotive force (EMF), is fundamentally related to the rate of change of magnetic flux (ΦB) through the coil.
EMF is equal to work done per unit charge or
EMF = work/charge = (force)(distance along coil)/charge = (F)(L)/q.
Recall the Lorentz Force expression for F (see my blog post: Lorentz Force Law)
F̅ = q(E̅ + (v̅ x B̅))
where
- F̅ = Total Force. The Lorentz Force
- F̅B = Force on charge q by magnetic field B
- F̅e = Force on charge q by electric field E
- q= charge
- v = velocity of charge
- E̅ = electric field
- B̅ = Magnetic Field
Substitute for F in the EMF expression (using the Lorentz Force Law) to get a general expression for EMF in a closed conducting loop.
Notice the q’s cancel out.
EMF=∮(E̅ + v̅ x B̅)⋅dL̄
where:
- EMF is the induced electromotive force (work per unit charge, in volts).
- E̅ is the induced electric field (a non-conservative field that arises from a time-varying magnetic flux, or the existing conservative electric field from charges).
- v̅ is the velocity of the conductor (the loop) relative to the magnetic field.
- B̅ is the magnetic field.
- v̅ x B̅ is the magnetic force per unit charge.
- dL̄ is an infinitesimal length element along the closed loop C.
- The integral ∮ is a line integral around the closed circular coil (or any coil really).
We are now ready to describe Motional EMF and Transformer EMF.
Motional EMF: Moving Conducting Coil and Stationary Magnetic Field
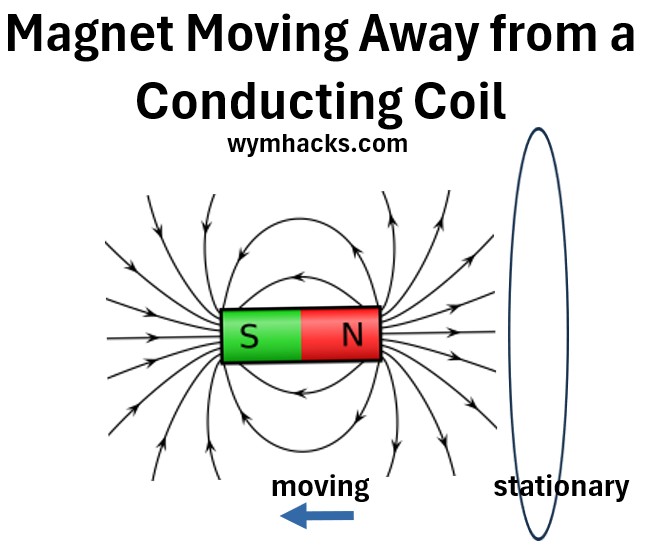
Picture: Conducting Coil Moving Away from a Magnet
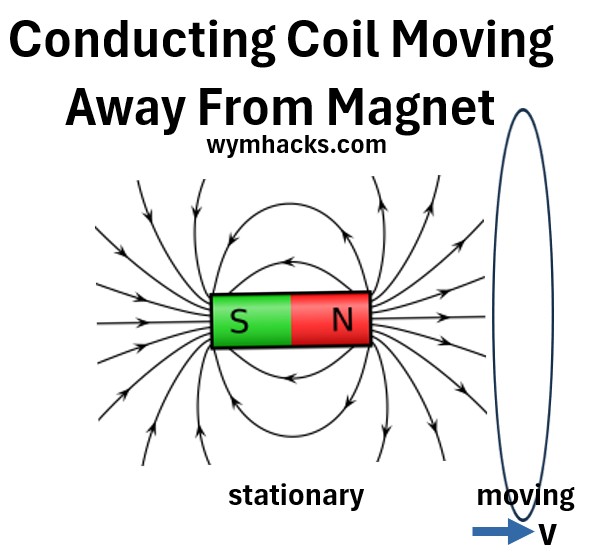
In this scenario, the coil is moved through a uniform, but spatially varying, magnetic field produced by a stationary magnet (or vice-versa), such that the flux through the coil changes.
So let’s start with our EMF equation:
EMF=∮(E̅ + v̅ x B̅)⋅dL̄
- The motion of the coil causes the term v×B to be non-zero only along the coil’s path through the field.
- The E field that arises in a moving conductor is electrostatic (conservative), meaning the net work it does on a charge moving around any closed loop is zero.
- Therefore, the E’s contribution to the net EMF (∮E̅⋅dL̄) is zero, and the entire EMF is due to the magnetic v×B force.
EMF=∮(v̅ x B̅)⋅dL̄ ; Motional EMF; Moving Conducting Coil over Stationary Magnetic Field
The moving charge carriers (q) within the coil experience a magnetic force due to their velocity (v) and the external magnetic field (B).
- This magnetic force per unit charge is v̅ x B̅.
- This force pushes the charges along the wire, driving the current.
- This is called Motional EMF.
- The work is done by the magnetic component of the Lorentz force per unit charge, v̅ x B̅, as it moves charges around the loop.
- Note that the magnetic force FB = q(v̅ x B̅) does no net work on the charge over time because it is always perpendicular to the charge’s instantaneous velocity (v),
- but it does work along the path of the wire to separate charges and establish the EMF.
Motional EMF: Expandable Coil in a Constant Magnetic Field
In the previous section we established a general expression for the EMF for a moving coil in a stationary magnetic field:
Motional EMF = ∮(v̅ x B̅)⋅dL̄
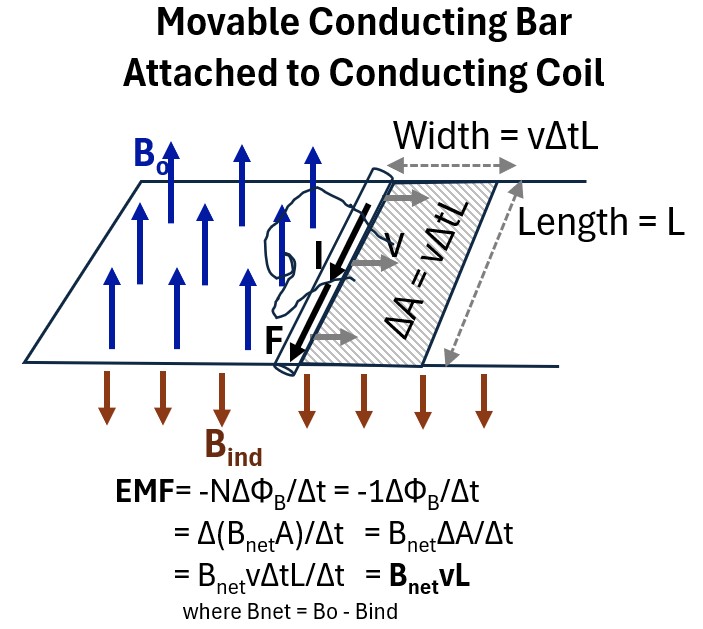
We can simplify this expression (i.e. get rid of the integral) if we assume we now have a conducting coil that is expandable via a moving rod that is connected to it.
It is placed (perpendicularly) into a fixed magnetic field Bo.
Picture: Movable Conducting Coil in a Fixed Magnetic Field
If we move the rod to the right
- for a duration of time Δt
- at a velocity v ,
- it will traverse an area ΔA equal to the product of the length of the bar (L) and the distance traversed (ΔA = vΔtL).
We are dealing with finite distances here so let’s use the average form of Faraday’s Law:
EMFavg=−NΔΦB/Δt
We also have an expression for magnetic flux:
ΦB = Magnetic Flux = (B)(Ap) =BAcos(θ) = B̄•Ā ; for Uniform B and Flat Surface where
Substitute for ΦB in the EMF expression to get:
EMF =−NΔBA/Δt = −BΔA/Δt
because
- cos(θ) = cos(0) = 1 and
- B is constant and
- N = 1 (just one coil)
Substitute for ΔA (with vΔtL)
EMF = −BΔA/Δt = −BvΔtL/Δt =−BvL
So
Motional EMF = −ΔΦB/Δt = −BvL ; Faraday’s Law for Fixed B and Perpendicular Expanding/Moving Coil
Notice that the current that is generated (I) by the moving rod will have a clockwise direction because:
- Lenz’s Law tells us that a counter acting magnetic field will be induced Bind .
- Use the right hand rule on Bind (fingers pointing down) to determine that the current will go in a clockwise direction.
- In the Feynman Lectures (ch.17),for a similar example, Bind is considered to be negligible for a weak current I.
- For completeness we can assume this is a Bnet value and we’ll just call it B.
So, in summary, looking at the drawing above, if we move the rod to the right at a velocity v,
- A motional EMF is produced (work or energy per unit charge) = BvL = (Force*Distance)/Charge
- Where B is a composite of the original magnetic field and any induced magnetic field (which is often assumed to be negligible in text book examples).
- So, a Force F is exerted on the electrons in the rod and pushes or moves the electrons (creating current I).
See this great video by Sal Khan: Emf induced in rod traveling through magnetic field
Ok, what about the scenario of a moving magnetic field and a stationary conducting coil?
Transformer EMF: Moving Magnetic Field and a Stationary Conducting Coil
In the last section we moved a coil over a stationary magnetic field and found that it is the v̅ x B̅ component of the Lorentz force that creates the EMF that causes the current to flow.
We want to imagine now that we are subjecting a stationary conducting coil to an changing magnetic field.
Picture: Moving Magnetic Field and Stationary Conducting Coil
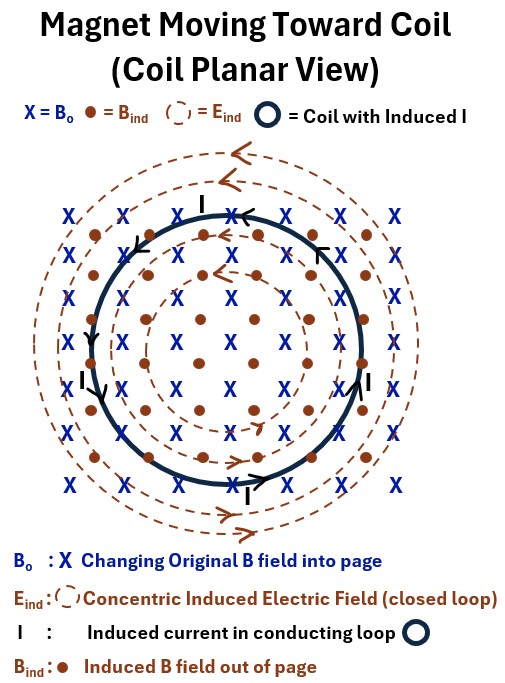
Let’s flip the picture so we have a plan view of the coil (looking down on it from above).
This is the view you see below where
- the solid black circle is the conducting coil and
- X represents the magnetic field going into the page (symbolized as the fletching, the back end, of an arrow).
Picture: Planar View: Changing Magnetic Filed with Fixed Conducting Coil
As Bo , the original or external magnetic field, changes, a current I will begin to “flow” in the coil.
What is the responsible force that makes this happen? Let’s start with our EMF general equation:
EMF=∮(E̅ + v̅ x B̅)⋅dL̄ ; EMF Expression Using the Lorentz Force Components
There are no moving electrons to begin with in this example, so the v̅ x B̅ term is zero!
EMF= ∮Ē•dL̄ ; Transformer EMF; Moving Magnetic Field and Stationary Conducting Coil
So it’s an Electric field E that forces the electrons around the coil.
- But, very importantly, this E field is NOT an electrostatic field (which is a conservative field)
- E is a very unique , looping, non-conservative Electric field that is able to push the electrons around as current.
More on this E field later , but now lets go through the sequence of events that occur after this E field is created (use the picture above as you read).
- Bo changes.
- A non conservative , looping, electric field Eind is induced.
- Eind forms concentric closed loop circles that move counterclockwise.
- This induces a current I which
- induces a magnetic field Bind
- We know Bind will be opposite Bo according to Lenz’s Law.
- This is represented as the brown dots in the drawing above indicating the induced B field is coming out of the page.
- We can then use the right hand rule (Right hand thumb towards I and curled fingers towards B) to determine the direction of I which will be counter-clockwise.
Let’s come back to the Eind .
Eind is not the same as the electrostatic E field, Eelectrostatic
So, in a changing magnetic field and a stationary conducting coil, an induced electric field is created and applies the force to move the current.
But Eind is distinctly different than the electrostatic field Eelectrostatic .
- Eind makes loops (like B fields); has no explicit charge source; not static and always changing
- Eelectrostatic is created by stationary static charges ; i.e. it starts and stops on a charge and is static
Eelectrostatic field lines extend radially outward or inward. These fields are conservative, which means the work done by the field on a charged particle moving in a closed loop is always zero.
- So we can say the closed loop line integral on the circuit (i.e. work done) is zero i.e. W/q = ∮Ē•dL̄ = 0
- This is because the force exerted by the field is independent of the path taken and
- only depends on the starting and ending points.
- This property allows us to define an electric potential, where the work done is simply the change in potential energy between two points.
Eind , generated by a changing magnetic field, are non-conservative.
- The work done by Eind on a charged particle moving in a closed loop is not zero.
- There will therefore be no well defined electric potential.
-
The EMF term, then, is W/q = ∮Ēind•dL̄
So we can write Faraday’s Law as follows:
∮Ēind•dL̄ = −NdΦB/dt ; Transformer EMF ; Faraday’s Law of Electromagnetic Induction (line integral form relating E to B)
-
This equation describes the phenomenon known as Transformer EMF (or non-motional EMF), where the electric field is induced by a time-varying magnetic field.
- Name: It has different names
- The Maxwell-Faraday Equation (Integral Form) – One of the four Maxwell Equations.
- Faraday’s Law of Induction – Most common and general name
- Physical Meaning: The line integral of the induced electric field (Eind) around a stationary closed loop is equal to the negative rate of change of the magnetic flux (ΦB) through the surface bounded by that loop.
- Requirement: The loop of integration (dL̄) must be stationary (fixed in space).
-
Eind is the electric field vector. It is an induced non conservative field (its not an electrostatic field).
- dL̄ is the infinitesimal vector of a path element along a closed loop.
- The direction of this vector is tangent to the path.
- ∮ is a closed line integral. It means you are summing up the dot product of Ē and dL̄ along an entire closed loop.
-
- The result of this integral is the electromotive force (EMF), which is the work done per unit charge in moving a charge around the closed loop.
- For induced electric fields, this value is non-zero, indicating that the field is non-conservative.
-
-
N: # of coils
- ΦB is the magnetic flux, which is a measure of the total number of magnetic field lines passing through a given surface
- dΦB/dt = Is the rate of change of magnetic flux with time
- −: The negative sign represents Lenz’s Law.
- It indicates that the direction of the induced electric field (and thus the induced current) will be such that it creates a magnetic field that opposes the change in the original magnetic flux.
- This is a fundamental statement of energy conservation in electromagnetism.
We also know that
ΦB = ∫sB̄•dĀ so let’s substitute this into the expression above to get
∮Ēind•dL̄ = −NdΦB/dt = -Nd/dt∫sB̄•dĀ ; Transformer EMF ; Faraday’s Law of Electromagnetic Induction (line integral form relating E to B)
The Differential Form (The Maxwell-Faraday Equation)
This is the most fundamental and generalized form, fitting in as the final piece.
It extends the concept from a physical loop to any point in space, showing that a time-varying magnetic field (B) creates a circulating electric field (E) at a fundamental level, even in a vacuum.
It is one of the four Maxwell’s Equations and is mathematically derived from the integral form using Stokes’ Theorem.
Please see how this is derived in my blog post: Maxwell Equations: From Integral to Differential Forms
∇×Ē=-∂B̄/∂t ; Faraday Equation (Differential Form)
This equation shows how fields themselves interact dynamically.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.