Last Revision: October 17, 2022
Summary
In seven graphs, this post shows 94 years of expected returns for various stock and bond allocations. These graphs plot annualized returns for 3, 5, 7, 10, 15, and 20 rolling yearly periods and show that:
- Variability of outcomes increases (risk increases) as the proportion of stocks relative to bonds increases. (left to right in each graph)
- The longer the holding period, the less the downside risk (smaller losses; see the trend as you go top to bottom through all the Graphs 2 – 7)
This kind of information can help investors decide on the proper stock and bond allocation that meets their risk/reward profile. But user beware, these graphs:
- are based on data going all the way back to 1928. This includes the 1929 crash recession and a few other tumultuous stock market periods that might not be repeated (Or they might. Nobody knows!)
- assume January to January periods. Other yearly periods have different return profiles e.g. February to February or July to July.
- are based on certain types and allocations of bonds
- are based on non normally distributed data sets, meaning interpreting the average and the standard deviation becomes a bit less clear.
- are based on past data and so don’t guarantee what future data will look like (a variation of bullet 1 really).
For this reason, don’t take the exact numbers in these graphs as gospel. Just grasp the general trends and use them to help you make reasonable decisions.
Menu
- Introduction
- Stock/Bond Allocation Expected Returns Methodology
- Importance of Context and Basis
- Rolling Return Calculation Methodology
- Historical Yearly Returns of Various Stock/Bond Allocations
- Example of How to Interpret the Graphs
- Rolling 3 Year Annualized Historical Returns
- Rolling 5 Year Annualized Historical Returns
- Rolling 7 Year Annualized Historical Returns
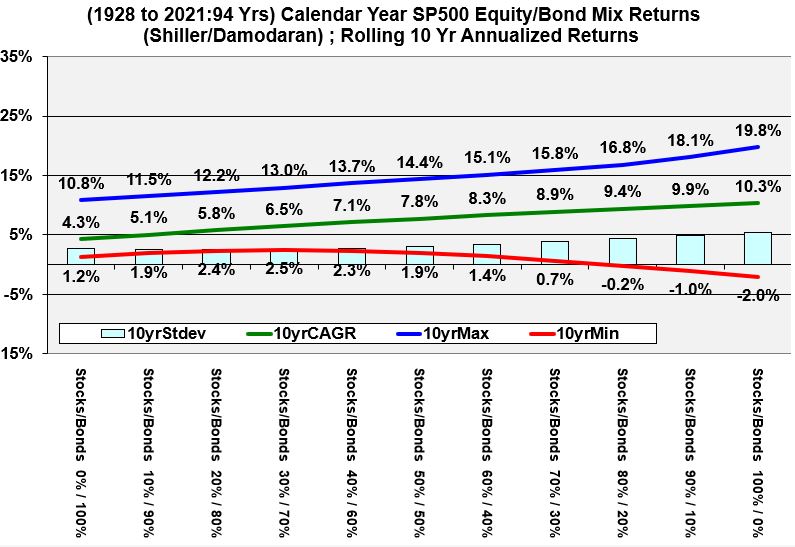
- Rolling 10 Year Annualized Historical Returns
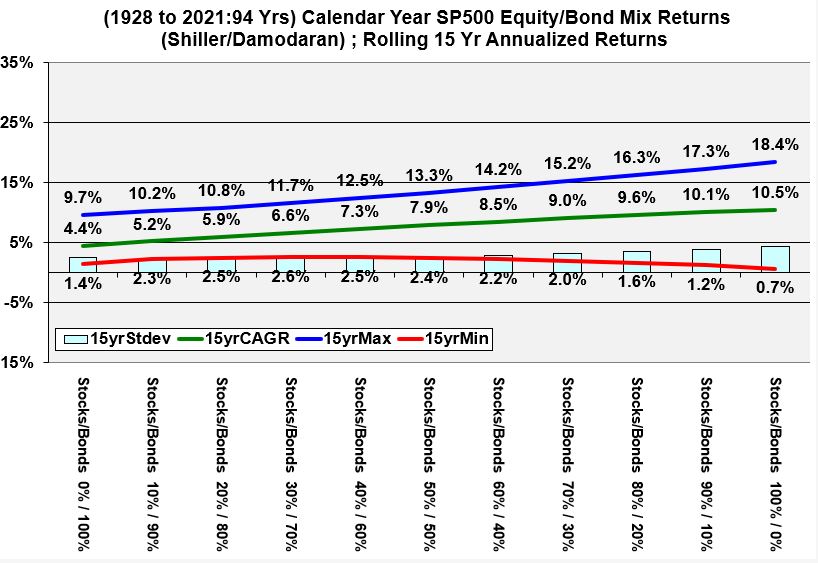
- Rolling 15 Year Annualized Historical Returns
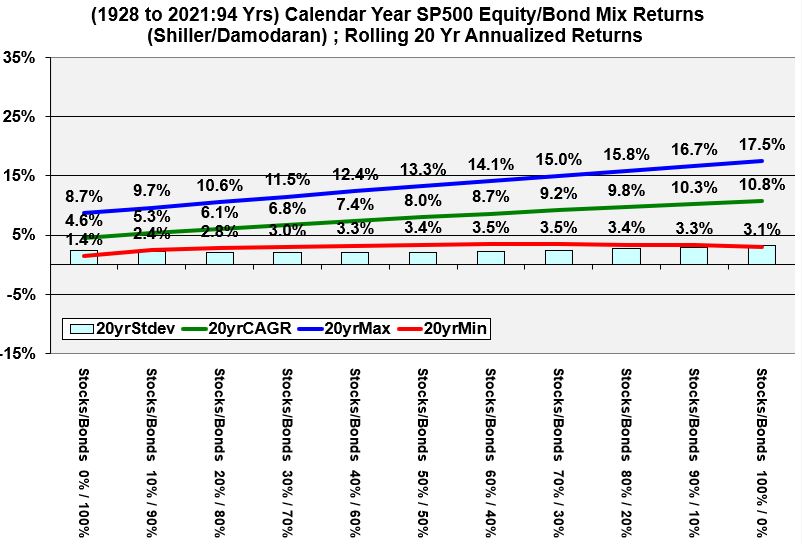
- Rolling 20 Year Annualized Historical Returns
- Analysis of the Historical Returns
- Conclusion
- Appendix (non-normal distributions)
Introduction
A fundamental question any investor has to answer is: “What balance of risky assets vs less risky assets should I choose?” The answer of course depends on the investor’s specific circumstances (age, tolerance for risk, financial and budgetary condition, etc.).
In this post we will look at stock and bond allocations as proxies representing the risk spectrum. There are other asset classes we could have used (e.g. real estate, commodities, specific stock types or sectors, etc.), however, at least for me, the big first question was: “Given that I have some money to invest and that I want to own stocks, what percent of my money should I allocate to stocks?” We choose bonds as the non-stock asset because these fixed income investments tend to be less volatile (but they also return less, especially in recent times). Also, if the methodologies described in this post make sense to you, you could apply them to other asset mixes as well.
If you’re curious about how I did the calculations, you can download and review these two spreadsheets
- Expected Stock/Bond Return Table Based on Shiller and Damodaran Data
- Annualized Expected Stock/Bond Returns for Various Rolling Periods
You can also accesses the related posts listed below. They should open into a separate tab so you can refer to them as needed.
Expected Returns of Bond and Stock Allocations Methodology
I downloaded two reference data sets from the internet to supply the raw data for this study:
- Monthly historical S&P 500 Index (and older related pre-1957 indices) returns from Robert Shiller which start in 1871.
- Yearly historical bond returns (Using 3 month Treasury Bills and 10 year U.S. Treasury Notes) from Aswath Damodaran which start in 1928.
I then
- converted the Shiller S&P 500 (and related pre-1957 indices) Index monthly returns into nominal yearly data using the January to January year periods. Be aware, as discussed in my S&P 500 performance post, that other calendar return periods will produce different numbers (e.g. February to February etc.).
- matched the Shiller yearly stock return list with Damodaran’s nominal historical 3 month Treasury Bill and 10 year Treasury Note performance list. Since Damodaran’s data starts in 1928, the matched list starts in this year (i.e. I don’t include 1871 through 1927 data).
- computed expected returns for each performance year for various mixtures of stocks and bonds assuming the bond component is 50% Treasury Bills and 50% Treasury Bonds. (expected return = % allocation stocks x % return stocks + % allocation bonds x % return bonds)
Data Context and Basis
Before we continue the methodology description, please get into the habit of always asking yourself, “What is the basis of the data or calculations that I am using?” Note that in this particular data set,
- I omitted several asset options (e.g. international stocks, corporate bonds, other alternative investments).
- I assumed a specific proportion of bond types to represent the bond investment (50/50 U.S. Treasury Bills and Notes respectively).
- I did yearly calculations and arbitrarily chose January to January periods.
- I assumed nominal returns (where inflation is included as opposed to real returns where values are inflation adjusted).
- I used data all the way back from 1928. The numbers would be different if I chose a data set starting in 1970 (we would have skipped the great recession caused by the 1929 crash).
Rolling Return Calculation Methodology
The methodology described in the previous section produces an expected stock/bond return table where the columns represent different stock and bond allocations (100% bonds/0%stocks to 0% bonds/100% stocks) in increments of 10%. The rows of the table represent each year, starting in 1928 and ending in 2021 (94 years of data). You can see the details by downloading my spreadsheet via the link in the introduction section.
Using this expected stock/bonds returns table, I computed annualized returns (using the CAGR formula) and descriptive statistics (e.g. average, min, max, standard deviation) for rolling 3, 5, 7, 10, 15, and 20 year periods. The resulting graphs are shown below.
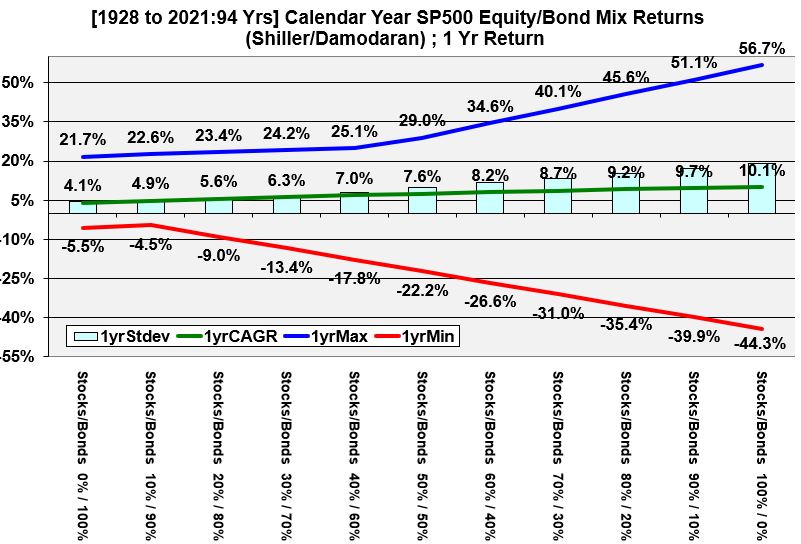
Historical Yearly Returns of Various Stock and Bond Allocations
Graph 1 below summarizes the expected returns table described above (using nominal returns for January to January calendar years of various stock and bond asset allocations over a 94 year period).
The average return (the CAGR) is represented by the Green line. This is bounded by maximum (blue line) and minimum (red line) lines. These lines show that as the stock allocation increases, the range of positive and negative returns also widen (i.e. the rewards and risks increase).
The bars in the graph represent the standard deviation, which is a way to describe risk in terms of variation from the mean (arithmetic average). Please be careful in how you interpret the standard deviation and the CAGR values since the return data set is not normally distributed. This means you cannot assume that the CAGR is the most likely value and you cannot assume that 1 standard deviation from the average will represent 68% of the data points. Please refer to the Appendix for more on this topic (see the “Non-Normal Distribution” section).
Historical Yearly Returns – Example of How to Interpret Graphs
Let’s take a look at a specific example and make sure we are interpreting these graphs correctly. Look at Graph 1 for a 50/50 bond/stock mix):
- The CAGR, Compound Annual Growth Rate, of the full 94 year period, for a 50/50 mix of stocks and bonds is 7.6%.
- Expect that at least 75% of the values will be within 2 standard deviations from the arithmetic average. Note that all the graphs show the CAGR and not the arithmetic average but these values are fairly close and very close as the period duration increases. The point here is, the “likelihood space” between the maximum and minimum values is pretty wide. Refer to the appendix under Chebyshev to understand the basis of this 75% rule.
- The maximum and minimum returns are 29% and -22.2%
Graph 1 (Historical Yearly Returns of Various Stock and Bond Allocations)
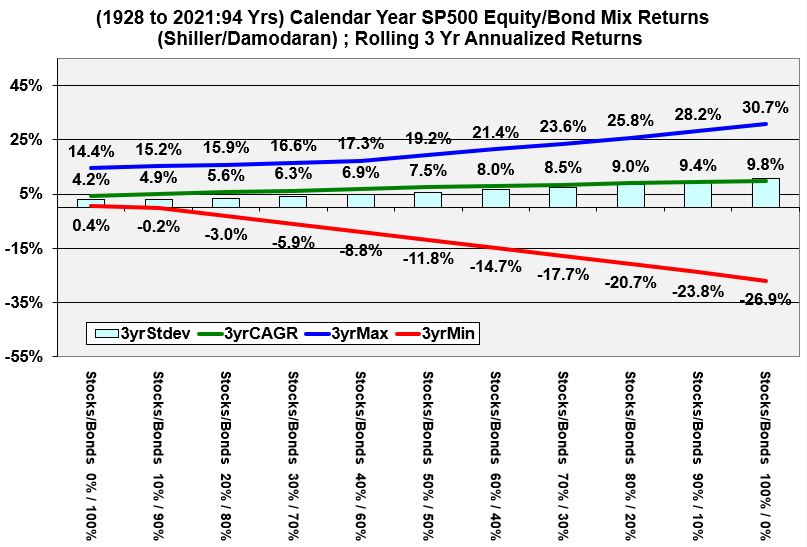
Rolling 3 Year Annualized Historical Returns of Various Stock and Bond Allocations
Graphs 2 through 7 below show annualized expected returns of bond and stock allocations for various rolling periods. As you look at the graphs, please notice that the
- riskiness always expands as we go from left to right on each graph (distance between minimum and maximum lines).
- the distances decrease between the maximum and minimum lines with increasing rolling periods.
- the red line eventually has only positive values in the 15 and 20 rolling year periods.
Graph 2 (Rolling 3 Year Annualized Historical Returns of Various Stock and Bond Allocations)
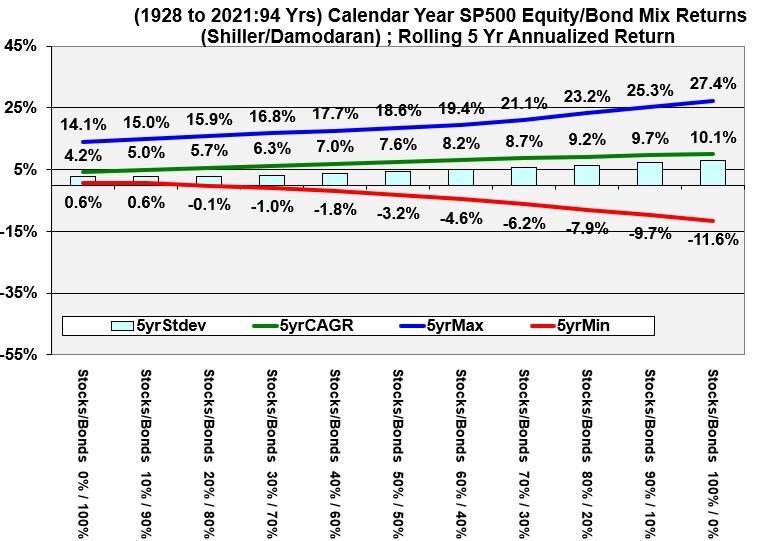
Rolling 5 Year Annualized Historical Returns of Various Stock and Bond Allocations
Graph 3 (Rolling 5 Year Annualized Historical Returns of Various Stock and Bond Allocations)
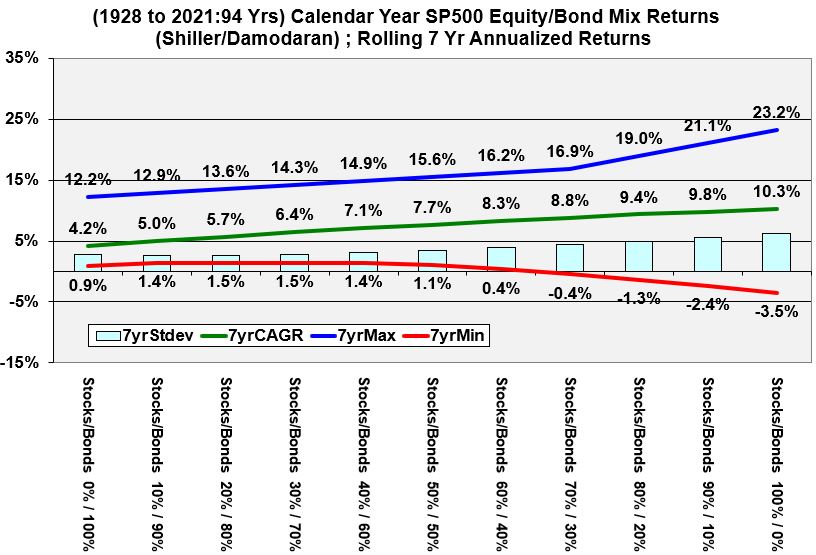
Rolling 7 Year Annualized Historical Returns of Various Stock and Bond Allocations
Graph 4 (Rolling 7 Year Annualized Historical Returns of Various Stock and Bond Allocations)
Rolling 10 Year Annualized Historical Returns of Various Stock and Bond Allocations
Graph 5 (Rolling 10 Year Annualized Historical Returns of Various Stock and Bond Allocations)
Rolling 15 Year Annualized Historical Returns of Various Stock and Bond Allocations
Graph 6 (Rolling 15 Year Annualized Historical Returns of Various Stock and Bond Allocations)
Rolling 20 Year Annualized Historical Returns of Various Stock and Bond Allocations
Graph 7 (Rolling 20 Year Annualized Historical Returns of Various Stock and Bond Allocations)
Analysis of the Historical Returns of Stock and Bond Allocations
The observations below are based on my interpretation of the graphs above. Please don’t construe my comments below to be specific advice for your particular situation. You need to do your own homework and make your own decisions.
- More stocks relative to bonds means a higher chance of making more or losing more money.
- Longer holding periods reduce the risk of losing money.
- Holding periods greater than 15 years don’t show any losses.
- For people who expect to hold investments for roughly 7 years or more, tilting towards a majority allocation to stocks might make sense. For example, in Graph 4, a 60/40 stock to bond allocation gives a minimum return of +.4%.
- For people who have a limited investment time horizon, using Graph 3 (rolling 5 year returns), for example, might guide them to a 30% – 50% stock allocation.
Conclusion
Studying historical annualized returns for varying bond and stock allocations can help you decide what the appropriate investment mix is for you. Your specific circumstances combined with your personality and investing psychology will probably require that you look at more than just a few graphs! But this kind of risk/reward data can definitely be a useful tool for your investment toolbox.
Appendix
Non-Normal Distributions – Example
In the S&P 500 performance post and in this post, we’ve noted that the data sets for these historical stock returns don’t show a normal distribution of data. A normal distribution is typically described by a Bell shaped symmetrical probability (frequency) vs data graph where points cluster in the middle and taper off evenly on each side of the center. Often we see bimodal (twin peaked distributions) and sometimes multi-peaked (multimodal) shapes to these investment return data sets.
A nice example that might explain why would be a bimodal distribution of test scores from two groups of students that we assume are the “same” but who have different teachers. One teacher has done a horrible job of teaching (we always blame the teacher don’t we?) and the other teacher is winning best teacher prizes left and right! Plotting the performance of these two classes would probably show up as a twin peaked bimodal distribution where the “left” shape represents one teacher’s class and the “right” shape, the other teacher’s class.
In the above example, an underlying phenomenon, “teachers with different teaching abilities”, is the main reason the bimodal shape exists.
Non-Normal Distributions – Investment Returns
Similarly, with historical investment returns spanning years and decades, there could have been several underlying phenomena that affected stocks in those time periods (e.g. wars, pandemics, and economic events like recessions). Recall from the S&P 500 performance post how devastating the aftermath of the 1929 stock market crash was.
With non-normal distributions, descriptive statistics formulas like the arithmetic average and standard deviation are still exactly correct. But rules using these terms when addressing normal distributions cannot be used. For example, for a normal distribution, it is expected that about 68% of the data points will be within 1 standard deviation of the mean and about 95% of the data points will be within 2 standard deviations of the mean.
So, for non-normal distributions, the descriptive statistics become a little more challenging to interpret. For example, the average might be roughly in the center of the data but it might not be anywhere near the most common value. Often the mode or even median might be more useful statistics. Plotting and observing the distribution graph should always be the first step when analyzing the data. Shape (skewness, modality, left and right tail shapes) and range of data (the X axis of the distribution chart basically) should be studied to see if any general conclusions can be made. Other statistical rules can be applied to non normal distributions as well (e.g. Chebyshev’s Inequality to determine % of data points occurring within certain standard deviations from the arithmetic average).
Non-Normal Distributions – Chebyshev’s Theorem
Chebyshev’s Theorem states that, for any number k greater than 1, at least 1 – 1/k^2 of the data values (for any kind of data set distribution) will be within k standard deviations of the mean. For example, for any distribution at least 1 – 1/2^2 = 75% of the values will be within 2 standard deviations of the mean.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.