Menu (linked Index)
Lorentz Force Law
Last Update: September 1, 2025
Introduction
The Lorentz force is the total force exerted on a charged particle that’s moving through a region containing both an electric field and a magnetic field.
This force is fundamental to electromagnetism and is responsible for many phenomena, including
- how electric motors work and
- how charged particles are deflected in particle accelerators.
In this post, we’ll describe this two part equation, and we’ll start with a review of some vector cross product rules and conventions.
Vector Cross Product Math Rules
Let’s denote c̅ = a̅×b̅ where
- a̅ = vector a
- b̅ = vector b
- c̅ = cross product of vectors a̅ and b̅
From vector math , we know that
- The vector c is perpendicular (orthogonal) to both a̅ and b̅
- Its direction is determined by the right-hand rule.
- There are actually three right-hand rule (RHR) methods that are equally valid
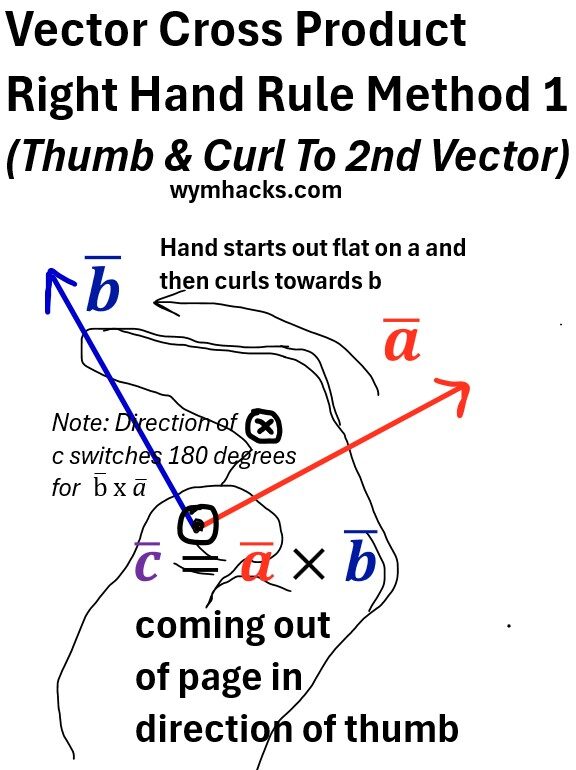
Vector Cross Product RHR Method 1
- Curl the fingers of your right hand from the direction of a̅
- to the direction of b̅ (through the smaller angle between them).
- Your thumb will point in the direction of c̅.
Picture: Vector Cross Product Right Hand Rule Method 1 (Curl Method)
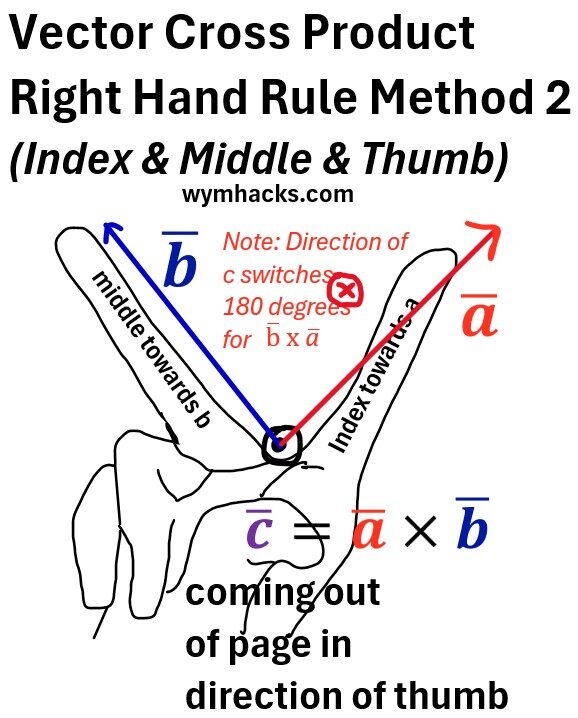
Vector Cross Product RHR Method 2
- Index finger towards a̅
- , middle finger towards b̅
- thumb points in direction of the cross product c̅.
Picture: Vector Cross Product Right Hand Rule Method 2 (Index, Middle, Thumb)
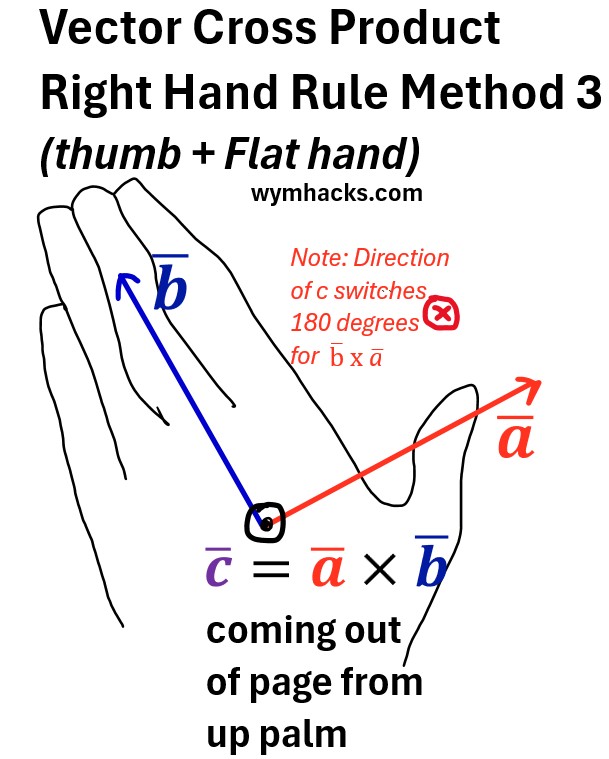
Vector Cross Product RHR Method 3
- Flat open hand, thumb towards a̅
- and other fingers toward b̅
- c̅ vector comes out of open palm side of hand.
Picture: Vector Cross Product Right Hand Rule Method 3 (Open Hand)
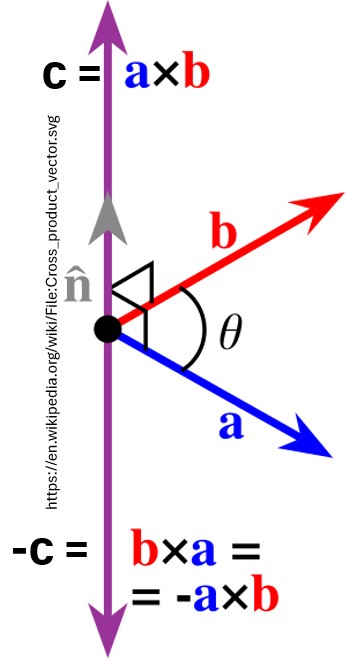
The magnitude of c̅ is given by the formula:
|c̅|=|a̅||b̅|sin(θ) ; Magnitude of cross product of vectors a̅ and b̅ (a̅ x b̅)
where
- θ is the angle between a̅ and b̅ (0≤θ≤π).
Picture: 3D Coordinates Vector Cross Product : c̅ = a̅ x b̅
Force on a Charge in an Electric Field
We can manipulate Coulomb’s Law to derive some useful expressions:
F̅e = kqtqs/r2 ; Coulomb’s Law
E̅ = F̅e/qt = kqs/r2 ; Electric Field
F̅e = qtE̅ ; Electric Force as a function of Charge and Electric Field
where,
- Fe = electric force (a vector)
- E = electric field = electric field strength = Force/Charge (a vector)
- qs = source charge (produces the electric field)
- qt = test charge (entering the electric field of qs)
- k = coulomb’s constant
- SI units for E: Newtons/Coulomb = N/C
- Other SI units for E = Nm/Cm = Volts/meter = V/m
- N = newton
- C = coulomb
- V = voltage
- M = meter
The schematic below shows a force F acting on a test charge qt in an electric field E.
- Remember that the F and E are vectors while q is a scalar.
Picture: Charge q in Electric Field E

Characteristics of a charge in an Electric Field
- A charge q placed in an electric field E will experience an electric force F.
- The direction of the force on a positive charge (q>0) is in the same direction as the electric field E.
- The direction of the force on a negative charge (q<0) is in the opposite direction to the electric field E.
- The magnitude of the force is directly proportional to the magnitude of the charge and the strength of the electric field.
Force on a Moving Charge in a Magnetic Field
Now let’s put a positive test charge q with a velocity v into a magnetic field B.
The force equation in vector notation is:
F̅B = qt(v̅ x B̅) ; Force on a Test Charge in a Magnetic Field (vector form)
The magnitude form of the equation is
FB = qtvBsinθ ; Magnitude of Force on a Test Charge in a Magnetic Field
Where
- FB = Force on charge q by magnetic field B
- qt = charge
- vBsinθ = magnitude of (v̅ x B̅)
- v = velocity of charge
- B = Magnetic Field
- θ = Angle between velocity and direction of B
Let’s rearrange the magnitude equation in terms of the magnetic field B:
B = FB/qtvsinθ
Let
- q = 1 Coulomb = 1C
- v = 1 meter/s = m/s
- θ = 90 degrees
Then the equation becomes B = 1 FB Newtons/(Coulomb-meters) = 1 FB Ns/Cm = 1 Tesla
- 1 Ns/Cm = 1 Tesla
So we can say that the magnetic field B is the force per 1 unit charge
where
- the charge is moving at 1 m/s and
- the charge is perpendicular to the magnetic field.
For example, B = 100 means 1 Coulomb of charge moving perpendicular to B at 1 m/s would experience a force of 100 N.
Picture: Force on a Moving Charge in a Magnetic Field

Some key characteristics of the Magnetic Force are:
- The magnetic force depends on the velocity of the charge.
- If v is 0, F is zero
- The magnetic force depends on the direction of motion.
- Since sin 90 = 1 is maximum, the maximum force occurs when the speed is perpendicular to the direction of B.
- The magnetic force direction is always perpendicular to the magnetic field B
- The electric force on the other hand is always parallel to the electric field E direction
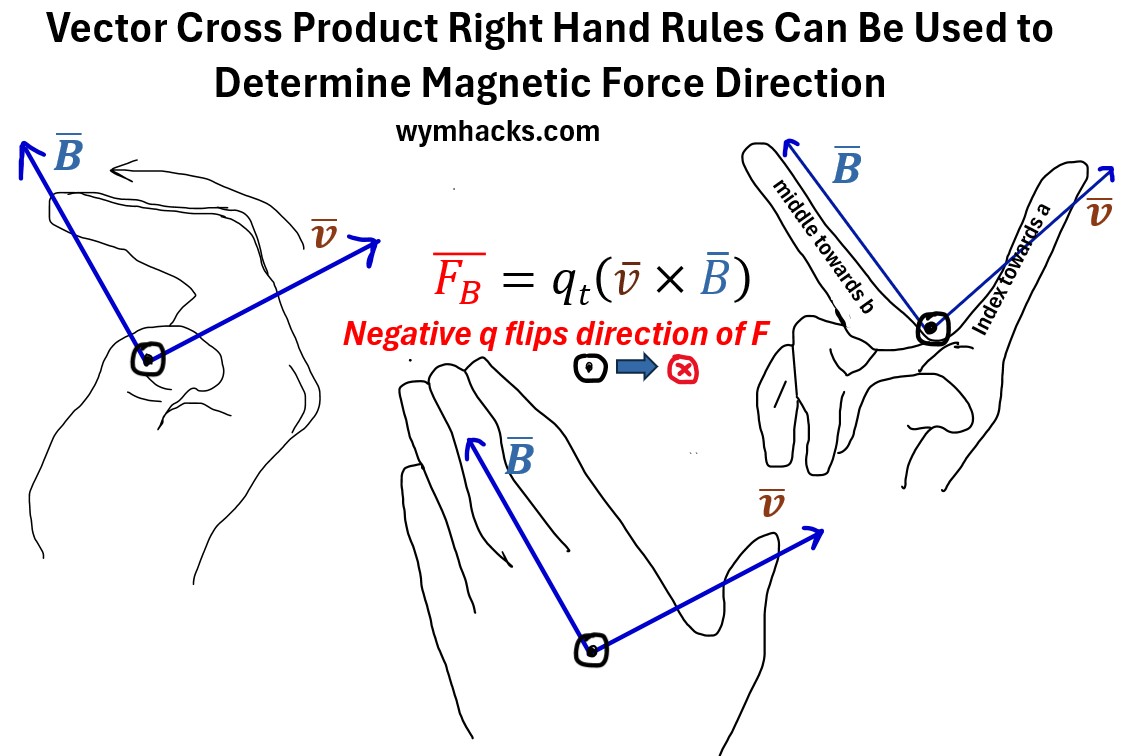
Application of the Cross Product Right Hand Rules
Because F̅B = qt(v̅ x B̅) and qt is a scalar, you can use any of the three Right Hand Rules to determine the direction of the Force component.
If the charge is negative, then the direction of F will flip.
Picture: Vector Cross Product Right Hand Rules Apply to the Magnetic Force on a Charge Equation
Synthesis of the Force on a Charge Expressions
In the 1890s, Hendrik Lorentz, a Dutch Physicist, was the first to combine these previously known electric and magnetic forces into a single, comprehensive law.
- The electric force component was known from Coulomb’s law, and
- the magnetic force component was formulated by Oliver Heaviside.
The Lorentz Force is the total electromagnetic force experienced by a charged particle moving through a region containing both an electric field (E) and a magnetic field (B).
The Lorentz Force Equation (Law):
F̅ = F̅e + F̅B
F̅ = qtE̅ + qt(v̅ x B̅)
or
F̅ = qt (E̅ + (v̅ x B̅))
where
- F̅ = Total Force. The Lorentz Force
- F̅B = Force on charge q by magnetic field B
- F̅e = Force on charge q by electric field E
- qt= charge
- v = velocity of charge
- E̅ = electric field
- B̅ = Magnetic Field
- θ = Angle between velocity and direction of B
Electric Force Component (qtE̅):
- represents the force exerted by the electric field E on the charge q.
- The force is parallel to the electric field for a positive charge (q>0) and flipped 1809 degrees for a negative charge (q<0).
- This force acts on the charge whether it is moving or stationary.
Magnetic Force Component (qt(v̅ x B̅)):
- represents the force exerted by the magnetic field B on a moving charge q.
- It is a vector cross product, which means the magnetic force is always perpendicular to both the velocity v and the magnetic field B.
- This force only acts on a charge if
- it is moving and
- if its velocity has a component perpendicular to the magnetic field.
- The direction is determined by the right-hand rule of which there are three methods.
View these excellent videos for more information:
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
