Menu (linked Index)
Magnetic Force on a Current Carrying Wire
Last Update: September 3, 2025
Introduction
A wire carrying current creates a magnetic field.
This magnetic field exerts a force on a magnet carrying compass.
Newton’s Third Law says that “for every action, there is an equal and opposite reaction.”
So we would expect an magnetic force to be exerted on a current carrying wire in a magnetic field.
The equation we need to compute this is the Lorentz Force Equation.
The Lorentz Force Equation
See my post Lorentz Force Law for more information.
One thing to get clear on first: The Lorentz force equation is a law.
- It’s called a law because it’s a fundamental principle derived from repeated experimental observations, not from more foundational theories.
- i.e. You can’t arrive at it through first principles (logically from other axioms or equations).
- So you have to start with the equation and you have to believe that it has been tested enough times and that, so far, it has not been proven false.
F̅ = F̅e + F̅B
or
F̅ = qE̅ + q(v̅ x B̅)
or
F̅ = q(E̅ + (v̅ x B̅)) ; The Lorentz Force Equation
where
- F̅ = Total Force. The Lorentz Force
- F̅B = Force on charge q by magnetic field B
- F̅e = Force on charge q by electric field E
- q = charge
- v = velocity of charge
- E̅ = electric field
- B̅ = Magnetic Field
- θ = Angle between velocity and direction of B
Lets assume we just want to look at the magnetic field B effects (No E).
Then
F̅B = q(v̅ x B̅) ; Magnetic Component of the Lorentz Force
Let v̅ = distance/time = L̅/t
Substitute for v̅ :
F̅B = q/t(L̅ x B̅) ; Magnetic Component of the Lorentz Force
But q/t is the current I so:
F̅B = I(L̅ x B̅) ; Magnetic Component of the Lorentz Force
which can also be expressed in magnitude form (remember your vector calculus rules):
FB= ILBsinθ ; Magnitude of Magnetic Component of the Lorentz Force (uniform B, straight wire, constant I)
where
- F̅B = magnetic force acting on wire
- I = constant current flowing through wire (in Amperes)
- L̅ = length or distance of wire segment inside magnetic field
- B̅ = magnetic field (in Tesla)
- F, L, B = magnitudes of F, L, and B
- θ = angle between L̅ and B̅ vectors
So, if you put a current carrying wire in a uniform magnetic field you might get a picture like the one below.
Picture: Magnetic Force on a Current Carrying Wire
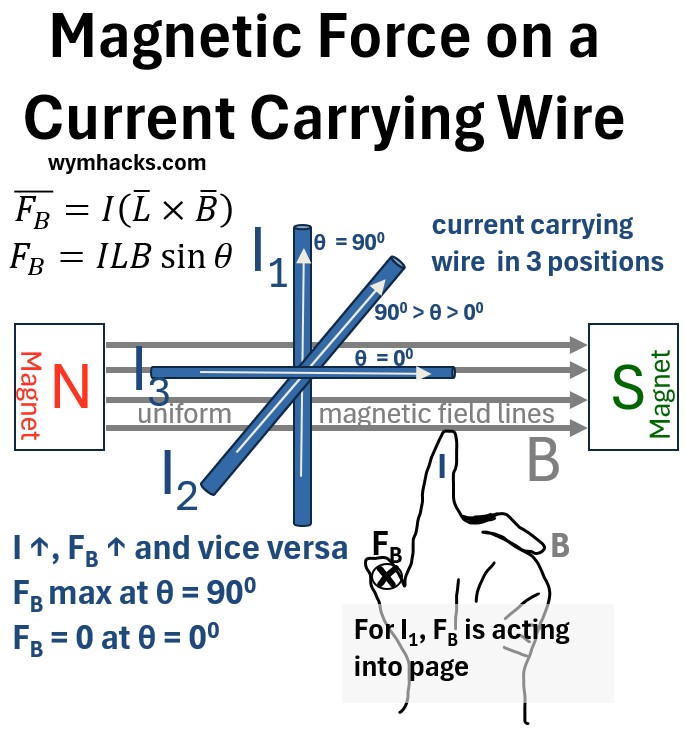
This setup will have the following properties:
- The wire in position I1 (90 degrees to the direction of B) will have the maximum magnetic force F acting on it
- The wire in position I3 will have zero F acting on it (it is parallel to the magnetic field B)
- Force will increase with increasing current I
- The direction of F depends on the direction of B and I
- For I1, the direction of F is into the page and perpendicular to B and I.
- The direction is determined by the cross product right hand rule
- Index finger pointed at L (which is in direction of I)
- Middle finger pointed at B
- Thumb pointed at F
Force on a current-carrying conductor in a magnetic field – Khanacademy – Mahesh Shenoy
Example: Magnetic Force on a Current Carrying Wire
An example of how this calculation might be done is provided in this great video: Magnetic force on a current carrying wire – Khanacademy – Sal Khan
The picture below is the set up for this example.
Picture2: Magnetic Force on an L meter section of Current Carrying Wire
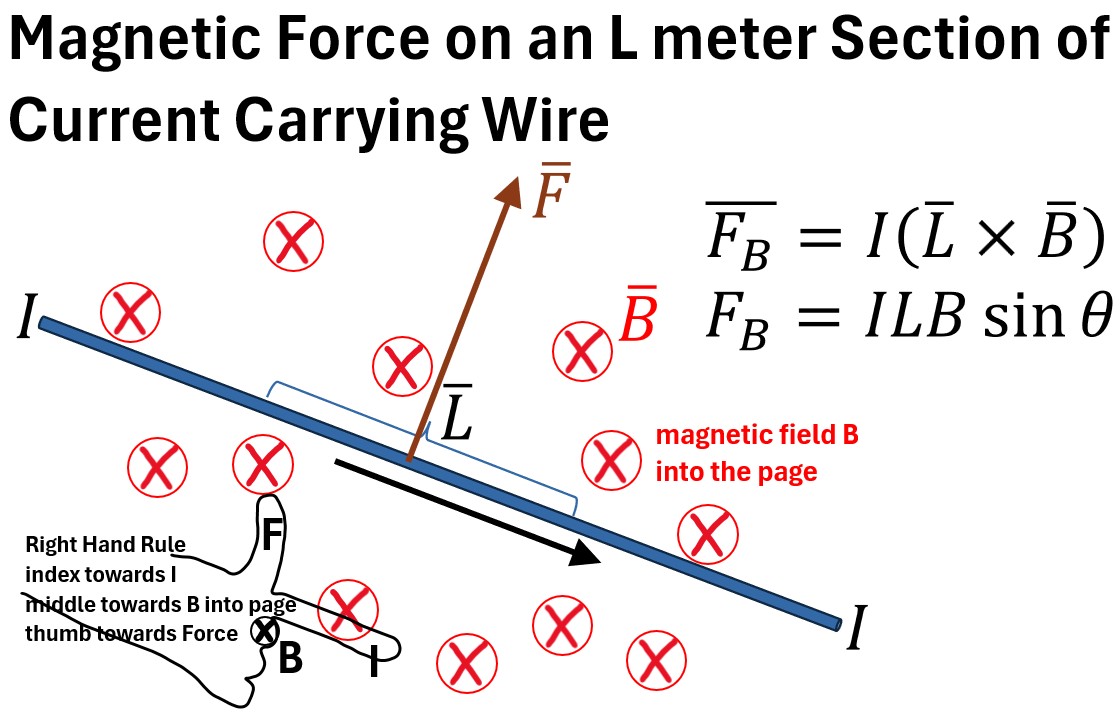
In the example depicted above,
- The magnetic field B is going into the page and
- the current carrying wire is placed in the field as shown with current I moving right to left.
- The force F acting on a section L (e.g. 2 meter section) of the wire will be perpendicular to the wire going up
- The direction of F is determined by the cross product right hand rule where
- Index finger points towards L (I)
- Middle finger points into the page in the direction of B
- The thumb then points upwards indicating the direction of the Force F.
Summary
A magnetic field’s ability to exert a force on a current-carrying wire has enormously important industrial applications.
It forms the fundamental principle behind many technologies like:
- Electric Motors: Magnetic fields exert torque on current-carrying coils, causing continuous rotational motion.
- Loudspeakers: A current-carrying coil attached to a cone moves within a magnetic field, producing sound.
- Galvanometers/Ammeters: Current in a coil within a magnetic field produces a torque, deflecting a needle to measure current.
- Relays: A current in a coil creates an electromagnet that pulls an armature to open or close contacts.
- Magnetic Levitation (Maglev) Trains: Magnetic fields lift and propel current-carrying coils on the train, or interact with currents induced in the track.
- Actuators (Solenoids): A current through a coil creates a magnetic field that pulls a ferromagnetic core or a current-carrying element, causing linear motion.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
