Last Update: February 23, 2023
Introduction: The Rule of 72
The rule of 72 is a useful way to quickly compute the number of years it will take to double an investment.
Rule of 72: Doubling Time in Years = 72/(annual rate of return entered as a %).
For example, if the rate of return on my $10,000 investment is 5%, it should double to $20,000 in about 72/5 = 14.4 years.
Use this rule for quick mental math (or back of the envelope) assessments. It is not exactly accurate but produces reasonable results if the annual rate is between 5 and 11%.
In this post we’ll derive the Rule of 72 and explore its accuracy.
The Rule of 72 Derivation
The Rule of 72 states that an investment, compounding annually, will double in about “72 / (Rate of Return)” years.
Example: A 10% annual compounding rate doubles my money in 72/10 = 7.2 years.
Derivation
Assume $1 and a yearly interest rate r.
- After one year we have: 1 x (1+r)
- After two years we have: 1 x (1+r) x (1+r) ;
- After n years we would have 1 x (1+r)n
- So how many years to double ?
- You have to solve 1 x (1+r)n = 2
- (1+r)n= 2
- Take natural log of both sides
- ln((1+r)n) = ln(2)
- n x ln(1+r) = .693
- For small r, ln(1+r) ≅ r for small r
- n x r = .693
- n = .693 / r
- n = 69.3/r% e.g. 8 percent return would be entered as 8 not .08
- Approximate 69.3 with 72 since this is divisible by 2, 3, 4, 6, 12, etc.
Accuracy of the Rule of 72
Recall from the previous section that the The Rule of 72 says n x r = 72 where n is the number of years required to double an investment and r is the rate of return (stated as a percent). And recall that it is derived from n x ln(1+r) = ln(2) = .693 where we assume ln(1+r) is roughly equal to r when r is “small”. Well what does small mean here? Lets do a rigorous analysis and see how accurate the Rule of 72 is.
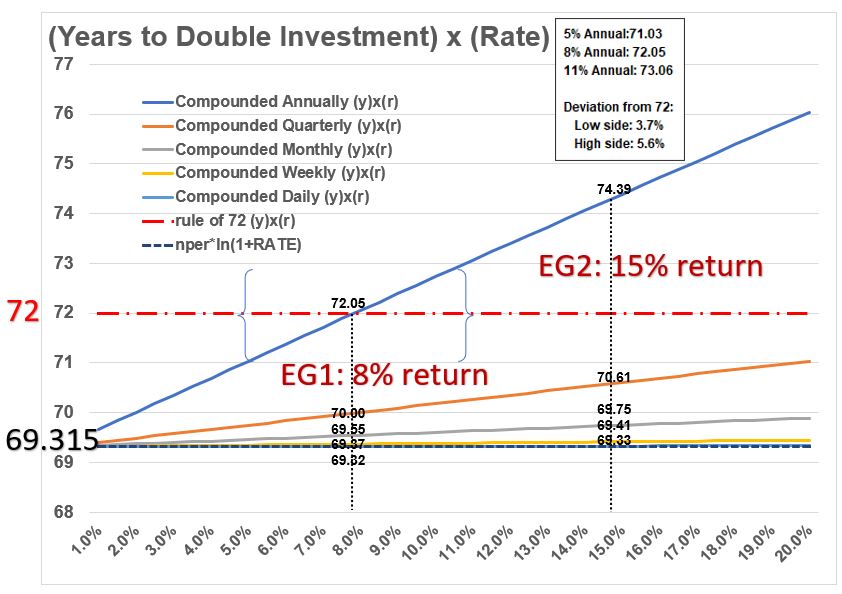
Refer to the Graph below as you read the following:
Years to Double Investment With Various Rates at Various Compounding Frequencies
Description
- The graph plots the rate of return (on the x axis) versus the product of the rate and the years required to double the investment.
- We can use the excel function NPER() or the relationship n = ln(2)/ln(1+r) to compute the actual doubling period.
- We can then multiply the actual doubling period by the rate to get a value we will express as a percent.
- We can plot these doubling period x rate values for various interest rates and compounding frequencies.
- There are two horizontal lines plotted on the graph. One is the rigorous value, n x ln(1+rate) = 69.315, and this is constant for any rate.
- The other horizontal line is our Rule of 72 assumption.
- All the other lines represent “n x rate” for various compounding frequencies
- All the compounding frequency lines slope upwards from left to right. The slope steepens as we go from daily compounding to annual compounding.
Annual Compounding Line
- The dark blue line is the annual compounding line. Its “n x r” value varies between 69.7 and 76 (for interest rates 1% and 20%). The change from 69.7 to 76 represents a 9% difference (going from lower to higher) or a 8.3% difference going from higher to lower. The point here, is that the actual value will vary from 72 depending on the rate and the compounding frequency. Look at the difference between 8% and 15% annual compounding in the two examples shown on the graph (72.05 vs 74.39 respectively).
- For the annual compounding line, the “n x r” value is about 72 for 8% (and its 71 for 5% and 73 for 11%. ). Applying the rule of 72 in this range will give you a reasonable accurate answer (of course , that depends on what accuracy you need).
- For higher compounding frequencies, the “n x r” values get closer to 69.3 which is the rigorous result of “doubling time” x ln(1+r).
Conclusions
- The Rule of 72, representing the “time to double x rate”, should be used as a rough rule of thumb. e.g. How long will it take me to double my money if my rate of return is 10% annually? Answer = 72/10 = 7.2 years.
- For a “time to double x rate” value of 72 “+or- 1” accuracy, use the rule of 72 for annual compounding periods with interest rates between 5 and 11%. (Refer to the Graph).
- For interest rates ranging between 1 and 20% and compounding rates ranging from daily to annually, the “n x rate” value will vary between 3.7% (on the low side) to 5.65% (on the high side) from the value of 72 (Refer to the Graph).
- For financial planning purposes, consider using excel time value of money functions in excel (e.g. NPER()), or a financial calculator, or on line calculators to produce more accurate numbers.
- In excel, use NPER(rate, pmt, pv, [fv], [type]), to compute the years needed to double a return (or have any other kind of return).
- On an HP12C calculator for example, you could enter values for i, PV, FV, to find a value for n.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
