Introduction
Snell’s Law (Law of Refraction) Example
Last Update: October 20, 2024
This post provides an example of how to compute refracted light angles using Snell’s Law.
Snell’s Law Application Example
Let’s use Snell’s Refraction equation, n2 sin θr = n1 sin θi , to determine the refracted light line angle based on other known values.
- the Angle of Incidence, θi , is the angle between the Incident Light Ray and the normal (dotted line) to the surface,
- and the Angle of Refraction, θr is the angle between the Refracted Light Ray and the normal.
- n1 and n2 are the indices of Refraction of medium 1 and 2.
the Index of Refraction n for each medium is defined as (speed of light in a vacuum)/(speed of light in the medium); n = c/v
Let light in air (n = 1) enter water (n = 1.33) at an angle of incidence of 60 degrees. Knowing three of the four variables in Snell’s equation we can calculate the angle of refraction to be 40.6 degrees. 
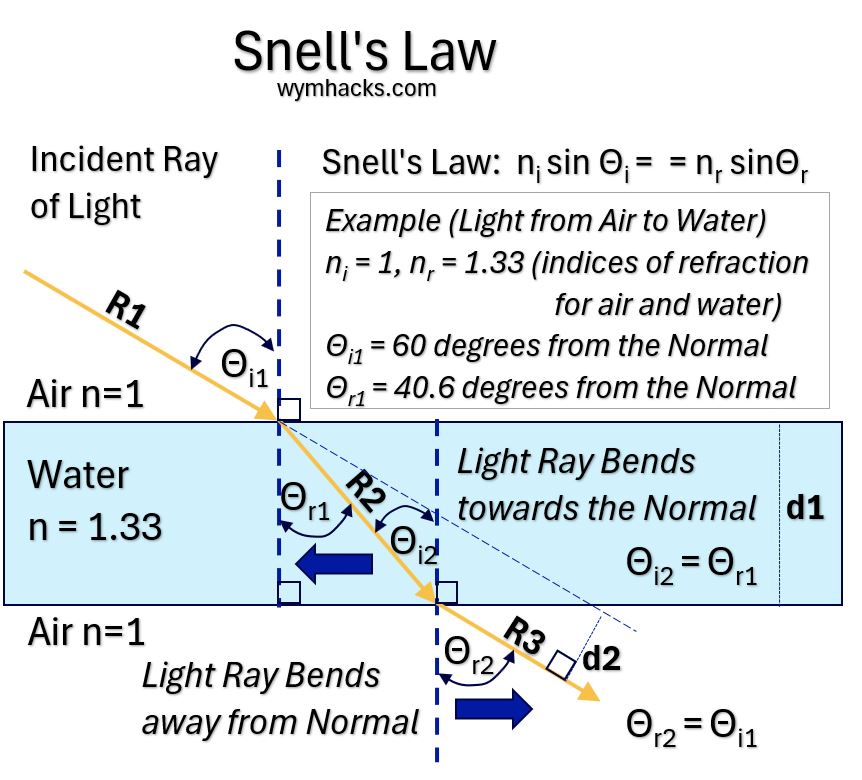
Notice that when the Light Ray exits into the Air again (Line R3 in the drawing above), it is parallel to the line R1 (Light Ray in air) but is offset by an amount d2. Using some basic geometry, this offset can be computed.
In the example above, we have two medium boundaries: Air(1)/Water(2) and Water(2)/Air(3)
We see that n1 < n2 in the computation , so the light ray R2 will bend toward the normal or perpendicular.
And, n2 > n3 in the computation, so the light ray R3 will bend away from the normal (perpendicular).
You should watch the videos below. Michel van Biezen is an excellent teacher.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
