Linked Menu
Last Update: March 9, 2024
Introduction
Time Value of Money
The Time Value of Money (TVM) Concept states that money tends to lose its value (purchasing power) over time. From this idea, we can mathematically define how the present and the future values of a thing or item relate to each other. The expressions can then be used to solve all sorts of financial problems (for an individual or for the biggest corporations).
Use the calculator tool embedded in this blog to compute Time Value of Money fixed-rate calculations. The tool is capable of accounting for fixed rate lump sum or constant periodic payments.
Time Value of Money Variables for Fixed Rates
The user can compute any one of the following variables, if any four of them are specified:
- i or r or RATE= rate per period. The rate is often a growth rate or an interest rate or a borrowing rate. We assume that the rate is fixed, that is, it is not growing over time.
- n or nper or NPER = number of payment periods
- PV = Present Value = current value
- PMT = Constant periodic payment = a constant, recurring outflow (-) or inflow (+) of money
- FV = Future Value = value some time in the future.
These kinds of calculations figure in to all sorts of personal financial decision making. For example,
- How much to save now and or periodically to be able to retire in the future
- Planning for education costs
- Planning for home mortgage payment and management
- etc.
Structure of Article
This article dedicates a few sections to the governing TVM equations as well as general instructions (and examples) on how to use the tool, but if you want to start calculating now, click here to jump right to the calculator.
So, let’s first define the TVM equations that the embedded calculator uses.
Time Value of Money (TVM) Equations
The governing equations for fixed rate Time Value of Money calculations are the
- Single Payment Compound Interest Formula (compounding and discounting forms)
- the PV and FV Ordinary Annuity and PV and FV Annuity Due equations
These equations relate the following variables to each other:
- rate per period (i or r or RATE)
- number of payment periods (n or NPER),
- present value (PV)
- fixed periodic payments (PMT), and
- future value (FV)
Refer to Appendix 1 for a listing of the equations and the variables involved. For an in depth review, read my article: Time Value of Money (TVM) Concepts, Formulas and Functions
General Steps for Doing TVM Calculations
If you want to skip to the calculator, click here.
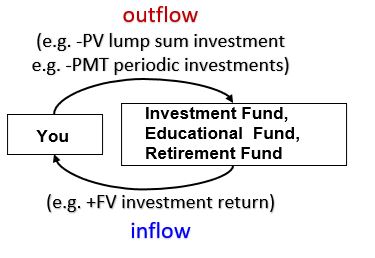
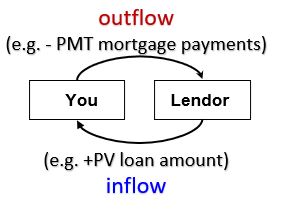
1 – Draw out a timeline (see Schematic 2 below) and populate it with your known and unknown TVM variables (PV, NPER, RATE, PMT, FV…see note). You must know 4 variables to compute the 5th. Values for (PV, FV, PMT) must be given a negative sign if the cash is a cash outflow. Think of a cash outflow as cash leaving or being subtracted from your pocket.
note: The TVM variables are noted in their Microsoft Excel format. Be aware that some of them are named differently on your financial calculator. On the HP12c calculator the variables are (PV, n, i, PMT, FV). The i here is rate per period = annual rate/compounding periods per year which we identify as “r” elsewhere.
Schematic 1: Sign Convention for PV,PMT, and FV in TVM Calculations
2 – Given y = total number of years and c = compounding periods per year, express the rate “r” as interest rate per compounding period (r= i/c). Also, express the number of compounding periods “n” as the product of compoundings/year “c” and number of years “y” (n = cy)
3 – Determine if you have an annuity calculation. If you have regular constant cash flows (i.e. PMT has a value), then this is an annuity calculation. If yes, you must identify the timing of the cash flow at the beginning of the compounding period (Annuity Due) or end of the compounding period (Ordinary Annuity).
4 – Given 4 of the 5 TVM variables, solve for the fifth variable. You can use a calculator with financial functions or software like Microsoft Excel or Google Sheets to do this.
If you want to skip to the calculator, click here.
Schematic 2 below, using a three year timeline as an example, establishes the general “rules” with respect to time when doing Time Value of Money (TVM) calculations.
Schematic 2: Generic TVM Guideline Using 3 Year Example

TVM Calculations: Timeline, Variables, Compounding Periods
- The convention is to always define today as time zero (0).
- Drawing a timeline isn’t essential for basic problems, but it’s a best practice and will help you establish the correct setup in more complicated problems.
- A TVM calculation always solves for one of 5 variables (PV, NPER, RATE, PMT, FV). You must know 4 TVM variables to compute the 5th.
- PV,PMT, and FV must be designated as negative values when they are cash outflows (think of cash being subtracted from your pockets). If PMT =0, then PV and FV need to have opposite signs.
- Typical compounding periods will be Yearly, Semi- Annually, Quarterly , and Monthly.
- The rate (RATE or i on your calculator) and the number of periods (NPER or n on your calculator) must always be consistent with the compounding periods per year. For example, if the compounding is done monthly, then the annual interest rate is divided by 12 and the number of compounding periods will be 12 x the number of years i.e. always enter the rate as rate per period.
Annuities
- With a Beginning of Year Payment (Annuity Due), the first payment is adjusted by the rate because it occurs at time 0.
- Annuities consist of regular periodic payments (PMT). Whenever there is a PMT value, you MUST define the cash flow timing (End or Beginning of period). Look at rows Ia. and Ib. in the schematic above to understand the difference between the two.
- Typical End of Period payment examples include (Ordinary Annuities) debt payments (mortgages, and loans) and savings contributions.
- Beginning of Period payment examples (Annuities Due) include rents, tuition, retirement income, rents, and lottery payments.
Calculators
- Use Microsoft Excel or Google Sheets or a financial calculator to do TVM calculations. Be aware that with financial calculators you typically enter the rate as a percentage form (e.g. you enter 5 for 5% and not .05) whereas with Excel or Google Sheets you enter the rate as a fraction (e.g. .05 for 5%).
- The tool embedded in this post is using Microsoft Excel.
- The order of inputs on your financial calculator is inconsequential. The order of inputs does matter however for Microsoft Excel and Google Sheets.
- You can also download free IOS or Android financial calculator apps (for you iphone) that mimic your calculator.
Nominal vs Real Returns
In another post (Historical SP 500 Index Performance Trends) we described the Nominal and Real long term returns of the S&P 500 stock index as 9% and 6.9% respectively. If you take the difference between the two, you will roughly approximate the inflation rate i.e. 9 – 6.9% = 2.1%.
Roughly, Nominal Rate – Inflation Rate = Real Rate.
- More accurately, if we let RN = Nominal Return, RR= Real Return, Ri = Inflation
- RN = (1+RR)(1+Ri)-1; Nominal Returns include the effects of inflation.
- RR = (1+RN)/(1+Ri)-1 = (RN– Ri)/(1+Ri)
- Real Returns are Nominal Returns adjusted for inflation
- Ri = (1+RN)/(1+RR)-1; If the Nominal and Real Returns are equal then there is zero inflation or Ri = 0.
- Read my blog “Inflation Rates, Real Returns, and Nominal Returns” for more details
So, back to our S&P 500 returns example, the inflation rate will be more like (1.09)/(1.069)-1 = 1.964%
Personal financial calculations can be done with Nominal Returns or Real Returns. The difference between the two is approximately the inflation rate, which indicates loss of purchasing power.
TVM Calculator Tool Introduction
If you want to skip to the calculator, click here.
The Microsoft Excel tool embedded in the following section can do basic TVM calculations for
- lump sum (single value) cash flows and
- multiple constant cash flows occurring at periodic (equal) intervals (i.e. fixed rate annuities).
Excel TVM Formulas Used by the Calculator
The calculator uses the following excel functions to compute the desired variable.
- =FV(rate,nper,pmt,[pv],[type]); if omit pmt, must include pv
- =PV(rate,nper,pmt,[fv],[type]); if omit pmt, enter fv
- =PMT(rate,nper,pv,[fv],[type])
- =NPER(rate,pmt,pv,[fv],[type])
- =RATE(nper,pmt,pv,[fv],[type],[guess]))
- When PMT>0, then must indicate type
- type = 0 (default, End of Period), 1(Beginning of Period)
HP 12c Calculator Functions
You could also use your financial calculator to do TVM calculations. When I set up the calculations in the embedded spreadsheet in this blog, I checked them by running the calculations on my financial calculator. I have an HP 12c calculator and its financial function buttons look like the following:
Use my article “Time Value of Money (TVM) Concepts, Formulas and Functions” for more on how to use the HP 12c calculator
The TVM Calculator Tool Embedded in this Blog is Easy to Use
- Go to Section 4 of the tool and choose from one of five calculator “boxes” depending on the variable you want to compute.
- You have the option of computing the Present Value (PV), the Future Value (FV), the constant and periodic cash payment (PMT), the fixed rate per period (RATE), or the number of payment periods (NPER). You have to know and enter four of the five values to get the desired fifth value.
- Just be careful that you enter the NPER (number of payment periods) and RATE (annual %/compounding periods per year) correctly.
- Also make sure that you’ve entered the correct signs for PV, PMT, and FV (+ = cash inflow, – = cash outflow).
- If you are solving for or including a PMT in the calculation, be sure to indicate the “type”. The “type” indicates the cash flow timing as happening at the end (0) or beginning (1) of the period.
TVM Examples Using the Embedded Calculator
This section shows 14 personal finance TVM computations using the online TVM calculator embedded in this blog.
Types of Problems the Calculator Can Solve
Positive Cash Flows
- Receiving Annuity Payments
- Take out a loan
- Lump sum future amount
- Income received
Negative Cash Flows
- Tuition payments
- Periodic savings or lump sum contributions
- Periodic repayments of debts
- Purchase of equipment or investment
End of Period Payments
Ordinary Annuities Examples:
- Debt payments(typically): e.g. auto, student, mortgage
- Savings contributions to retirement savings for eg.
Beginning of Period Payments
Annuities Due Examples:
- Lottery payments
- Rents
- Tuition
- Retirement Income
Examples Using The Embedded Calculator
Lump Sum (Single Value) Present and Future Value Examples
Example 1:
Invest $25,500 now. Calculate the value after 35 years if the investment compounds annually at 7%.
Use the FV Calculator.
- NPER_35
- RATE_7%
- PV___$25,500
- PMT__$0 (i.e. no periodic payments)
- FV___-$272,253 (rounded)
- type__0 End of Yr pmt
- Since PMT is 0, “type” is not used in the calculation. It is assumed that FV will be an end of year payment.
- Assume that the return is Nominal (includes inflation) unless it is specifically stated as Real (does not include inflation).
Example 2:
Invest $25,500 now. Calculate its value after 35 years if the investment compounds monthly at 7%.
- NPER_420 (c x n = 12 x 35 = 420)
- RATE_0.5833% (i/c = 7%/12 =.5833%)
- PV___$25,500
- PMT__$0.0
- FV___-$293,407 (rounded)
- type__0 End of Yr pmt
- Note that the RATE cell only shows two digits passed the decimal but it will accept and calculate as many decimals as you want. You can enter into the cell as a computation as well i.e. “=.07/12”
- Since PMT is 0, “type” is not used in the calculation. FV will be an end of year payment.
- NPER = 35×12=420 and RATE = 7%/12=.5833% NPER and RATE values MUST be consistent with the monthly compounding.
- Effective Annual Interest Rate = (1+Stated Annual Interest Rate/c)c -1 = (1+.07/12)12-1 = 7.229%, Where c is number of compounding periods per year. The Effective Annual Interest Rate will be progressively higher than the stated inflation rate (annual basis) as the number of compounding periods per year increases. Learn more about the Effective Rate in my blog Time Value of Money (TVM) Concepts, Formulas and Functions
Example 3:
You have a 5 year old that you want to send off to college in 13 years. You want your kid to go to UT Austin because , no pressure, everyone in your family going back to the 1800s has attended and graduated from UT. The average yearly cost for attending UT today is about $20,000/year but costs are increasing at a yearly clip of 8%. What can you expect to pay for a year at UT when your Child is 18? You might want to take some indigestion medicine before you find out.
- NPER_13
- RATE_8%
- PV___$20,000
- PMT__$0
- FV___-$54,393 (rounded)
- type__0 End of Yr pmt
- Since PMT is 0, “type” is not used in the calculation. FV will be an end of year payment.
Example 4:
What initial investment today will produce $1 million in 35 years if you can return 7% compounded annually on this investment?
- NPER_35
- RATE_7%
- PV___-$93,663 (rounded)
- PMT__$0
- FV___ $1,000,000
- type__0 End of Yr pmt
- Since PMT is 0, “type” is not used in the calculation. FV will be an end of year payment.
Example 5:
What rate of return will double your $25,000 initial investment in 10 years?
- NPER_10
- RATE_7.18%
- PV___-$25,000
- PMT__$0.0
- FV___ $50,000
- type__0 End of Yr pmt
- Since PMT is 0, “type” is not used in the calculation. FV will be an end of year payment.
- Your PV and FV inputs must be opposite signs to honor the cash flow convention (- = out and + = in). You’ll get an error message otherwise.
- See my blog on the Rule of 72 which is a shortcut you can use when you are doing these kinds of calculation (Doubling Time in Years = 72/(annual rate of return entered as a %).
Example 6:
The St. Louis Fed shows that the Consumer Price index was 37.9 in January 1970 and 300.536 in January 2023. What is the inflation rate over this period?
- NPER_53 (the period 1970 to 2023 covers 53 years)
- RATE_3.98%
- PV___-$37.9
- PMT__$0.0
- FV___ $300.5
- type__0 End of Yr pmt
- Since PMT is 0, “type” is not used in the calculation. FV will be an end of year payment.
- PV and FV must be entered with opposite signs. Follow the cash flow convention (cash out = – and cash in = +)
Example 7:
How many years will it take to double your $50,000 investment, if you can return 9% compounded annually?
- NPER_8.04
- RATE_9%
- PV___-$50,000
- PMT__$0.0
- FV___ $100,000
- type__0 End of Yr pmt
- Since PMT is 0, “type” is not used in the calculation. FV will be an end of year payment.
- Beware, if you are using an HP12c calculator, the n (NPER) will output 9. It rounds the accurate number of 8.04% to 9% which might be too inaccurate for practical use!
- If you multiply NPER x RATE you get 72.36. Have you heard of the Rule of 72? In order to double an investment, the following relationship can be derived: NPER x ln(1+RATE) = .693. To simplify this equation you can assume that ln(1+RATE) is roughly equal to RATE. So roughly, NPER x RATE = .693 = 69.3%. Approximate 69.3% with 72% since this is divisible by 2, 3, 4, 6, 12, etc. We end up with an approximation called the Rule of 72 that states: To double your investment, NPER x RATE roughly equals 72.
Annuity Examples
Personal financial calculations often involve annuities which have periodic (equal interval) payments. The examples below are annuity calculations in which the rate and payments are fixed.
Example 8:
You have $10,000 dollars saved up. How much do you need to add at the END of each year, to have $2,000,000 in 35 years? Assume your overall annual investment return is 6%.
- NPER_35
- RATE_6%
- PV___-$10,000
- PMT__-$17,258
- FV___$2,000,000
- type__0 End of Yr pmt
- Notice that PV was entered as a negative value (cash flow out) and the resultant PMT ,which is a cash outflow, is negative as well.
- On a 12C HP calculator you would make sure to select the “g” followed by the “end” buttons (it’s the default mode, so make sure to change this to Beg if it’s a beginning of year cash flow aka Annuity Due).
Example 9:
How much will you have in 35 years if you have $10,000 invested today and you add an additional $20,000 at the End of each year? Investment returns are 7%.
- NPER_35
- RATE_7%
- PV___-$10,000
- PMT__-$20,000
- FV___$2,871,503.4
- type__0 End of Yr pmt
Example 10:
You have an investment worth $500,000 today. You want to make withdrawals at the Beginning of the next 15 years. Investment returns are 8%. How much will you be able to withdraw? Assume all the money is withdrawn.
- NPER_15
- RATE_8%
- PV___ -$500,000
- PMT__$54,087.8
- FV___0
- type__1 Beg of Yr pmt
- If you had chosen type 0 = end of period, the PMT would be $58,414.8. Do you see why it is a bigger number? For the same inputs, Ordinary Annuities (end of period payments) will always be higher than Annuity Due payments (beginning of period payments). Also notice that (54,087.8)(1.08) = 58,414.8.
Example 11:
How much do you need to deposit today in order to withdraw $50,000 at the END of each year for the next 10 years. Assume the deposit returns 7% annually and assume all the money is withdrawn.
- NPER_10
- RATE_7%
- PV___$351,179.1
- PMT__-$50,000
- FV___0
- type__0 End of Yr pmt
Example 12:
You win a $275,000 lottery award that you will receive as a lump sum . You want to invest it and receive 25 yearly payments (at the beginning of the year) until the funds are depleted. Assume your investment rate is 6%. What yearly amount can you expect to receive?
- NPER_25
- RATE_6%
- PV___-$275,000
- PMT__$20,294.7
- FV___0
- type__1 Beg of Yr pmt
Example 13:
You want to borrow money to buy a house. You can get a $500,000, 30 year fixed rate loan at 5.5% annual interest (stated interest). What will your mortgage payments be if the interest is compounded monthly and your payments are made monthly. Mortgage payments are typically paid in arrears (End of period).
- NPER_360 (30 years x 12 compounding periods/yr)
- RATE_0.4583% (5.5%/12 = .4583%)
- PV___$500,000
- PMT__-$2,838.9
- FV___0
- type__0 End of period pmt
- NPER = 30 years x 12 compoundings/yr = 360; RATE = 5.5% Annual Return/12 periods =.4583%. In the calculator entry cell, you can type an equation as well as enter the value itself. So in this example ,you could have typed “=30*12” in the NPER cell and “=5.5%/12” in the Rate cell.
- For much more on home mortgages check out my blogs (1) Mortgage Calculation Primer and (2) Mortgage Calculation Tool
Example 14:
Your 2 year old Child will attend college in 16 years when she is 18. You estimate that college costs today (i.e. current college cost) will be $20,000/year. (1) How much money would you need today if your money earned 8%/year and if college costs increase 6%/year? (2) What yearly investment would you have to make to meet these college costs if your last investment payment was at the start of your child’s first college year?
Schematic Eg14.1 – Education Cost and Investment Timeline Example
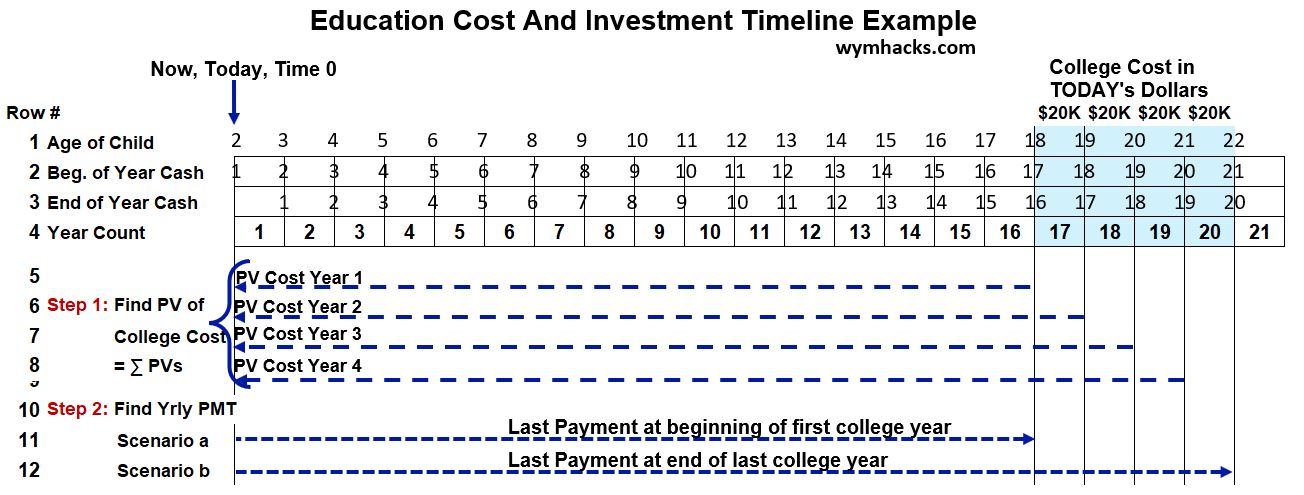
Solve this problem in two steps.
- First , compute the present value of all cash flows at time 0 (today).
- Then given this PV, you can compute the yearly payment based on when you want the payments to stop. In the timing chart above I show two example options (Scenario a at the beginning of the first college year and Scenario b at the end of the fourth college year).
Step 1 (method 1) : Determine the present value of college costs. There are two ways to do the calculation. The first way is to (a) inflate the college costs to their actual year costs and then (b) discount them using the actual rate (Nominal Rate).
- (a) Use the compounding equation to estimate the actual costs in future college years:
- Yr. 17 College Cost = $20,000(1+6%)16 = $50,807
- Yr. 18 College Cost = $20,000(1+6%)17 = $53,855.5
- Yr. 19 College Cost = $20,000(1+6%)18 = $57,086.8
- Yr. 20 College Cost = $20,000(1+6%)19 = $60,512
- (b) Discount each of the actual (Nominal) costs above to the present using the discounting equation (let PV = Present Value):
- PV Yr. 17 College Cost = $50,807.0/(1+8%)16 = $14,830.1
- PV Yr. 18 College Cost = $53,855.5/(1+8%)17 = $14,555.5
- PV Yr. 19 College Cost = $57,086.8/(1+8%)18 = $14,285.9
- PV Yr. 20 College Cost = $60,512.0/(1+8%)19 = $14,021.4
- (c) Due to the Additivity Principal ( see analystprep.com), the total PV will be the sum of the above so PV Total Cost = $57,692.8
Step 1 (method 2): Determine the Present Value of the college costs by discounting the current (today’s) costs using the Real Return (which removes the effects of college cost inflation). The Real Return is defined as:
RR = (RN–Ri)/(1+Ri) where RN Ri and RR = Nominal Return, Inflation Rate, and Real Return respectively. In this example RR = (8% – 6%)/(1+6%) = 1.887%
- Method 1 steps (a) and (b) above collapse into four calculations that produce the same numbers as Method 1 (b) and (c).
- PV Yr. 17 College Cost = $20,000/(1+1.887%)16 = $14,830.1
- PV Yr. 18 College Cost = $20,000/(1+1.887%)17 = $14,555.5
- PV Yr. 19 College Cost = $20,000/(1+1.887%)18 = $14,285.9
- PV Yr. 20 College Cost = $20,000/(1+1.887%)19 = $14,021.4
- PV Total Cost = sum of above = $57,692.8
Step 2: Compute the yearly payments PMT. From Schematic Eg14.1, if the last payment is at the beginning of the student’s first year, then NPER = 16. We’ll use the PV from Step 1 (57,692.8), assume an 8% actual rate of return, and depletion of the money so FV = 0.
- NPER_16
- RATE_8%
- PV___$57,693
- PMT__-$6,518
- FV___0
- type__0 End of period pmt
So, the yearly payment will be $6,518.
Conclusion
You can figure out a lot of practical personal financial questions by using the time-value-of-money (TVM) tool embedded in this article.
A few major advantages to using this tool are:
- All you need is an internet connection to run it.
- You don’t need to buy and learn how to use a financial calculator and
- You don’t need to learn how to use spreadsheets (From Excel at a cost or from Google for free).
Solve for One of Five Financial Variables
The embedded tool is an Excel spreadsheet calculator that requires you to enter four of five variables to compute the fifth. The five variables are:
- n = NPER = Number of compounding periods.
- i = RATE = Rate per period = (Annual % Rate)/(Number of compounding periods per year). The RATE is assumed to be fixed.
- PV = Present Value = the current value = the value now. Must be properly signed (+ = cash inflow, – = cash outflow)
- PMT = Constant and periodic payment properly “signed” (i.e. enter it as a negative value if it’s a cash outflow). We assume the PMT is fixed and not growing.
- FV = Future Value. Must be properly signed (+ = cash inflow, – = cash outflow)
- Remember, enter four to get the fifth.
I’ve provided 14 practical examples of how you can use the calculator to compute financial metrics that might be important to you (e.g. how will your money grow? How much will a mortgage or a college education cost? How much do you need to save for retirement? etc.)
Build Your Financial Competence
The simple calculator embedded in this blog empowers you to get solutions (or at least options) to many personal financial questions . Read some of my other articles (see list below) to get a more in-depth appreciation of the Time Value of Money:
Appendix 1 – Time-Value-of-Money (TVM) Governing Equations (for Fixed Rates)
The governing equations for fixed rate Time Value of Money calculations are the
- Single Payment Compound Interest Formula (compounding and discounting forms)
- the PV and FV Ordinary Annuity and PV and FV Annuity Due equations
Equation details and variable definitions are provided below.
Please refer to my article Time Value of Money (TVM) Concepts, Formulas and Functions for an in depth review.
Single Payment Compound Interest Formula
Table 1: Single Payment Compound Interest Formulas and Factors

F = P(1+r)n = P(1+i/c)cy
Where,
- F = Future Value, P = Present Value,
- i = yearly interest rate (sometimes called the stated rate)
- c = number of compounding periods per year
- r = interest rate per compounding period = i/c
- y = number of years
- n = total number of compounding periods = (c)(y)
- This is called the Compound Interest Formula for a Single Cash Flow
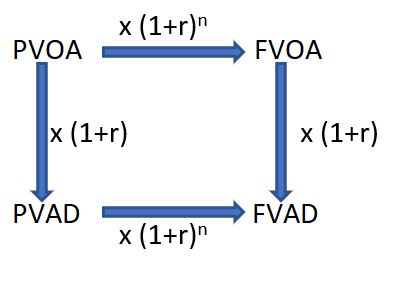
PVOA – Present Value Ordinary Annuity
Annuity payments are constant period payments. An Ordinary Annuity has end of period payments.
P = X/r ( 1 – 1/(1+r)n )
Present Value Ordinary Annuity (PVOA)
Where,
- P = Present Value of all payments
- X = constant payment
- r = interest rate per compounding period = i/c
- i = yearly interest rate (sometimes called the stated rate)
- c = number of compounding periods per year
- y = number of years
- n = total number of compounding periods = (c)(y)
PVAD – Present Value Annuity Due
Annuity payments are constant period payments. An Annuity Due has beginning of period payments.
P = X/r ( 1 – 1/(1+r)n ) (1+r)
Present Value Annuity Due (PVAD)
Note that the Present Value Annuity Due = (Present Value Ordinary Annuity)(1+r)
- P = Present Value of all payments
- X = constant payment
- r = interest rate per compounding period = i/c
- i = yearly interest rate (sometimes called the stated rate)
- c = number of compounding periods per year
- y = number of years
- n = total number of compounding periods = (c)(y)
FVOA – Future Value Ordinary Annuity
Annuity payments are constant period payments. An Ordinary Annuity has end of period payments.
F = X ( (1+r)n – 1) /r
Future Value Ordinary Annuity (FVOA)
Where,
- F = Future Value of all payments
- X = Constant Payment
- r = interest rate per compounding period = i/c
- i = yearly interest rate (sometimes called the stated rate)
- c = number of compounding periods per year
- y = number of years
- n = total number of compounding periods = (c)(y)
FVAD – Future Value Annuity Due
Annuity payments are constant period payments. An Annuity Due has beginning of period payments.
F = X ( (1+r)n – 1)(1+r) / r
Future Value Annuity Due (FVAD).
Note that Future Value Annuity Due = (Future Value Ordinary Annuity)(1+r)
- F = Future Value of all payments
- X = Constant Payment
- r = interest rate per compounding period = i/c
- i = yearly interest rate (sometimes called the stated rate)
- c = number of compounding periods per year
- y = number of years
- n = total number of compounding periods = (c)(y)
Convertibility between Ordinary Annuities and Annuities Due
An Ordinary Annuity equation can be converted to its Annuity Due form by multiplying it by (1+r) where r is the interest rate.
A Present Value Annuity equation can be converted to it Future Value form by multiplying it by (1+r)n