Euler’s Formula Derivation

Leave a Comment / Math / By

Menu (linked Index)

Euler’s Formula Derivation

Last Update: December 12, 2024 

Introduction

In this post I’ll take you step by step through the derivation of Euler’s Formula

 

and its famous cousin, Euler’s Identity

Euler’s formula states that for any real number x, eix = cosx + isinx , where

  • e, Euler’s Number, is a constant approximately equal to 2.71828….
  • e is the base of the natural logarithm,
  • i is the imaginary unit (), and
  • cos and sin are the trigonometric functions cosine and sine.

Euler’s identity is a special case of Euler’s formula obtained by setting x = π.

Where 

  • π is a mathematical constant approximately equal to 3.14159 and
  • is the ratio of a circle’s Circumference to its Diameter (C/D).

It states that eiπ + 1 = 0, which simply and elegantly relates five fundamental mathematical constants: e, i, π, 1, and 0.

You can learn more about related topics via my other posts listed below:

Return to Menu

The Derivative

I’m going to define enough math for you here to enable you to follow and understand every step of my Euler’s Formula derivation. 

If you want to give your brain a precious gift, go to Khanacademy.org and review some of the introductory Calculus material.  

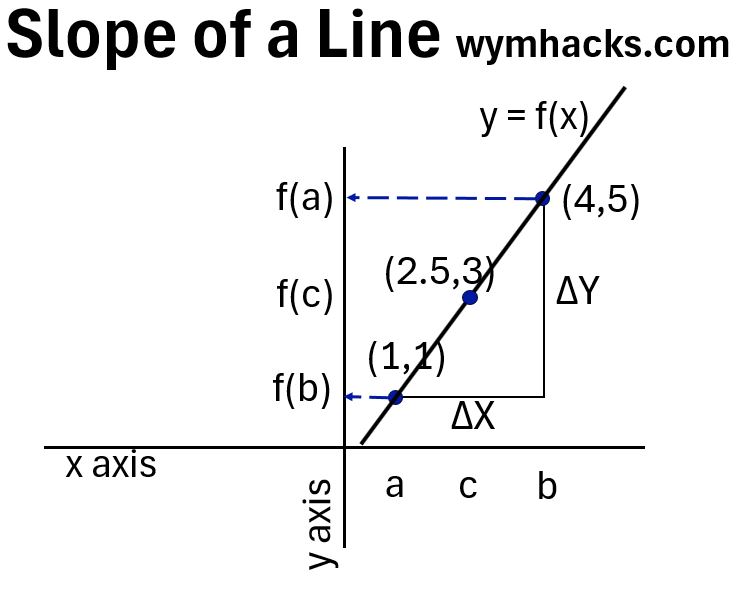
Slope of a Line

The slope of a line is the “rise over the run” i.e. (the change in y)/(the change in x) = Δy/Δx in a Cartesian coordinate system. 

In the graph below, the slope of the line y = f(x) can be defined by the two points (4,5) and (1,1) where we are using (x,y) notation on a Cartesian coordinate system.  

Graph_Slope of a Line y=f(x)
 

The slope using points a and b will be = Rise/Run 
= Δy / Δx = (f(a) – f(b)) / (b-a)

= (5-1)/(4-1) = 4/3 = 1.33

Lines by definition have the same slope , so we’ll get the same slope for any other pair of points. 

If we use points c and b
= (3-1)/(2.5-1) = 1.33
= (5-3)/(4-2.5) = 1.33

What if we wanted to find the slope of a curve?

Slope of a Curve

Consider the curve in the graph below. 

Graph_Slope of a Curve

 

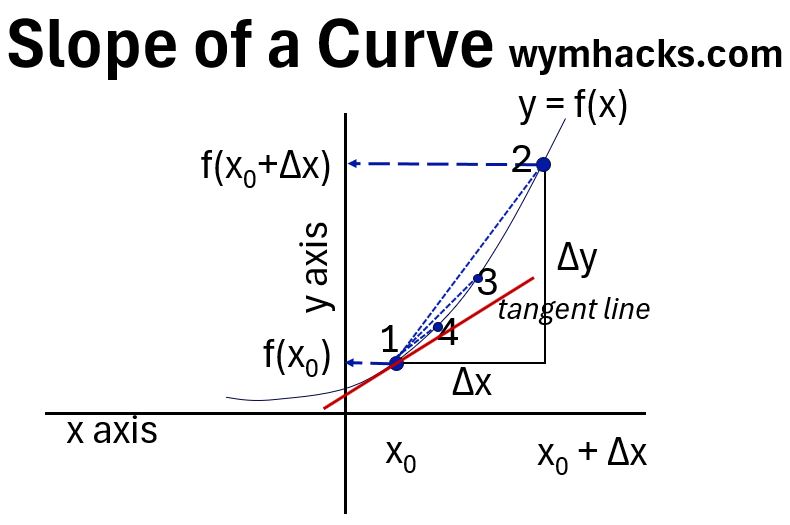
The Curve at each point has a different slope. So, What is the slope at point 1?

We still need two points to compute a slope so let’s choose Points 1 and  2 (see graph above).  

  • Slope 1 to 2  = Rise/Run = ∆y / ∆x
  • Will give the slope of the Secant Line 12 (the dotted line between the two points in the graph)

This slope will not be very accurate. 

We could compute the slope of Secant Line 13. It’ll be better but will still be off.

We could improve on this and compute the slope of  Secant Line 14.

Ideally, if we could make the distance between the x points , ∆x, infinitely small, we would get the true slope at point 1. 

We call this the slope of the tangent line at point 1 or  the derivative of y = f(x) evaluated at point 1. 

The general formula for a derivative states that

  • as the limit of the difference in x values goes to zero, 
  • the slope will be equal to the (change in f(x))/(change in x).  

or

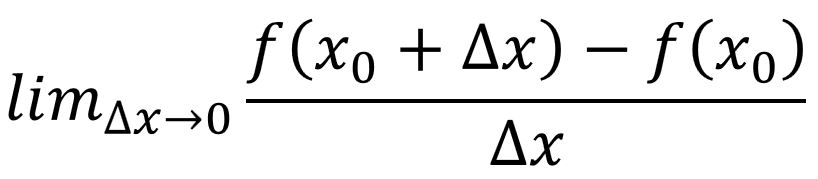
Derivative Generic Formula

We can notate the derivative in a few ways:

  • Derivative of f(x)
  • f prime x or f'(x) ; Lagrange Notation
  • df(x)/dx = dy/dx; Leibniz Notation
  • slope of tangent line at x

For a curve, each point has a unique tangent line with a unique slope (a unique derivative).

Check out these two nice introductory videos on the derivative:

Derivative Rules

I’ve listed some of the main calculus derivative rules below.

Use Khanacademy.org’s excellent videos to learn more about these.

The primary rule for derivatives is the power Power Rule and is defined as follows:

Power Rule:  d/dx(xn) = nxn-1  where n cannot be zero.

For example, the derivative of 3x3 is 3*3x2 = 9x2

Here is a summary of the main derivative rules including the Chain Rule which is very useful.

Table_Some Derivative Rules

Some Derivative Rules 1

Derivative Chain Rule

 Return to Menu

Derivatives of Some Useful Functions

We’ll also run into some functions we’ll need to take the derivatives of.

These are equalities that you would basically have to memorize if you were taking a calculus class.

 
Table_Derivatives of cosx, sinx,ex, and lnx

Ok, we are intellectually armed and ready. 

Return to Menu

Taylor and Maclaurin Power Series

Power Series

note: The equation numbers in this main text are  consistent with the equation numbers in the detailed derivations in Appendix 2. 

Consider the Power Series 

(1) f(x) = c0 +c1x + c2x2+ c3x3+ c4x4+… cnxn

which we can ‘shorthand’ as

(2) 

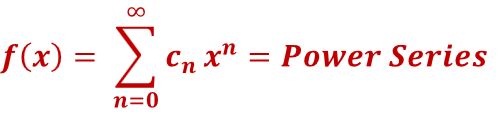
Notice that when -1 <x <1 , equation (2) becomes the Geometric Power Series.

(3)

But back to equation (2). 

Characteristics of the Power Series:

  • It continues indefinitely (infinitely)
  • The c terms are constants and
  • n represents the nth power (from 0 to infinity).

Shifting the Polynomial

Let’s change the form of equation (2) a little bit and replace the x terms with (x-a). 

We’re just shifting (see Appendix 1) the polynomial so all of the non-constant terms go to zero at x=a.

So (2) becomes,

(4) 

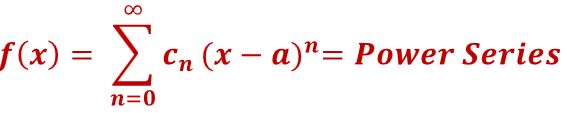
Find an Expression for The Coefficients

We want to find expressions for the coefficients cn and we can elegantly do this by

  • taking f(x), the first derivative of f(x), and continuously higher derivatives of f(x) and
  • evaluating each of them at x = a.

This approach effectively allows us to isolate each coefficient from the others and express it as a function of the derivative.

It’s a lot easier to derive it then to describe it ,so go to Appendix 2 to see the full derivation (where equations (5) through (15) are developed).

This is what you get for cn:

(15) 

where,

  • cn = nth coefficient
  • f(n) = nth derivative of a function (where f(0) = f)
  • a = the point being evaluated
  • n! = n factorial = 1*2*3*…*n  (for n>0;  0! = 1)

Taylor Series

Substituting equation (15) into equation (4) gives
 
(16) 
 
Equation (16) is a power series called the Taylor series for the function f at a (or we can say “f about a” or “f centered at a”).
 
where,
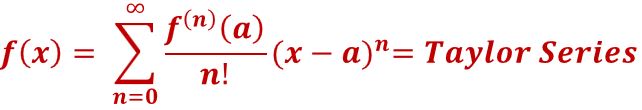
  • ∑ = summation from n = 0 to ∞ (infinity)
  • f(n) = nth derivative of a function (where f(0) = f = the function itself)
  • a = the point being evaluated
  • n! = n factorial = 1*2*3*…*n  (for n>0;  0! = 1)

Pretty Cool.

For a Taylor series to exist at a point a, the function must be infinitely differentiable at that point.

This means that all derivatives of the function, from the first derivative to infinitely many derivatives, must exist at a.

Maclaurin Series

If we assume that a=0 in the Taylor Series equation (16), we get:

(18)

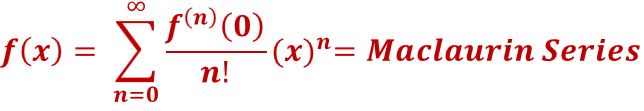
Equation (18)  is a power series called the Maclaurin Series for

the function f at 0 (or we can say “f about 0” or “f centered at 0”)

Where,

  • ∑ = summation from n = 0 to ∞ (infinity)
  • f(n) = nth derivative of a function (where f(0) = f = the function itself)
  • n! = n factorial = 1*2*3*…*n  (for n>0;  0! = 1)

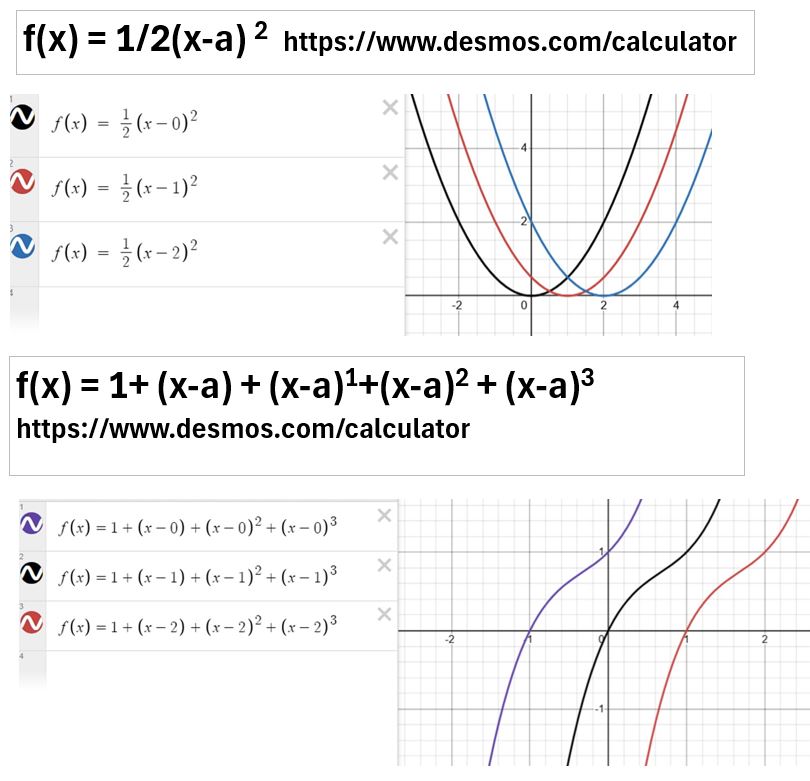
Graphical Meaning of the Taylor Series Terms

Look at the first four terms of the Taylor Series evaluated at x = a:

Graphical Meaning of Taylor Series Expansion

Check out the graphs below where I plot the Maclaurin Series approximation for y = ex evaluated at a = 0.

Picture_Maclaurin Series of the Exponential Function y =ex

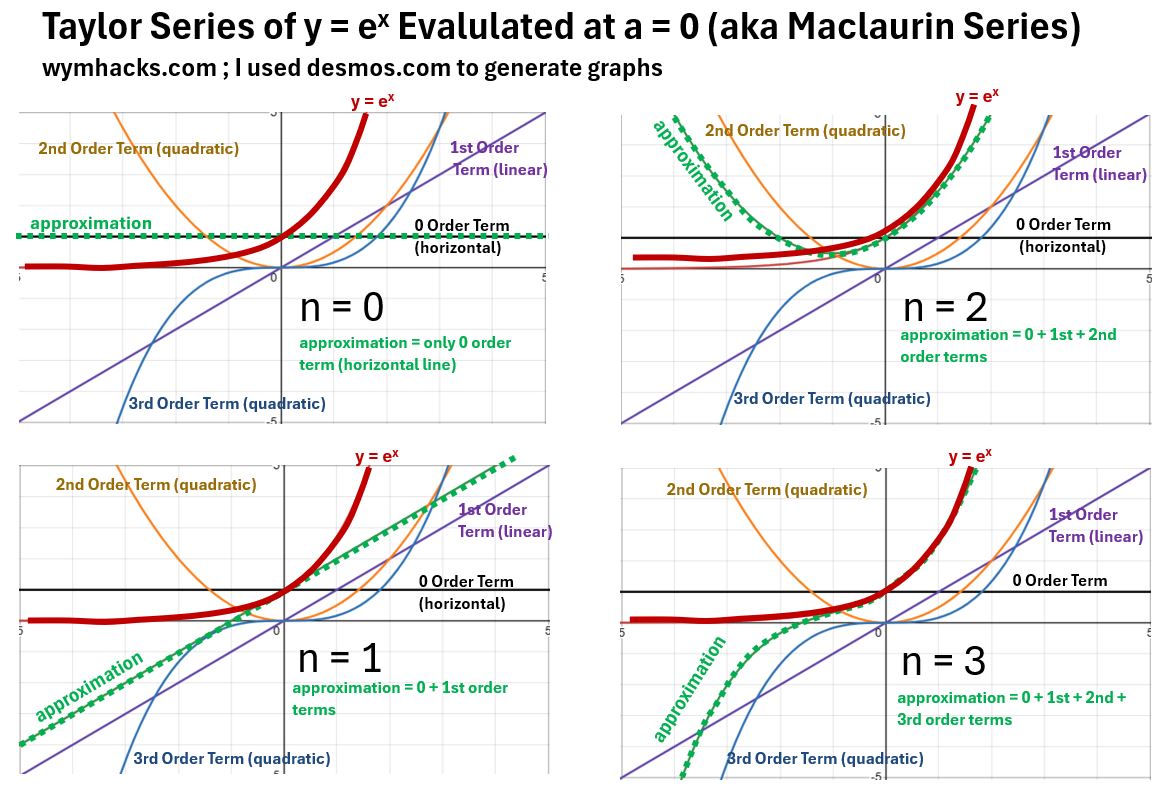
  • If I plot the zero-th order term (n=0) only , the Maclaurin series  approximation is going to be the horizontal line at y = 1. 
  • If I plot the approximation to be the sum of the 0th and 1st order term (n = 1), it will be a tangent line. 
  • This tangent line is the sum of the horizontal line at y = 2 and the 1st order term (the purple line in the n = 1 chart)
  • If I expand the series to include the 0th + 1st + 2nd terms, the approximation will be a parabola as shown in the n = 2 graph. 
  • This parabolic approximation is the sum of the linear horizontal 0th order term (black line), the linear 1st order term (purple), and the parabolic 2nd order term (orange)
  • Expanding the approximation to include the 0th, 1st, and 2nd terms gives the approximation shown in the n-3 chart.  
  • You can see the approximation is pretty good around zero and greater. It does start to deviate sharply on the negative side. 
  • Choosing the point a, then is important. You want to choose a point in the region of interest, to ensure you get an accurate estimate.  

Derivation of Euler’s Formula

In this section we’ll derive Euler’s Formula:  eix = cos x +  i sin x where

To do this, we need to develop the Maclaurin Series for cosx, sinx, and ex.

We need to know the following derivatives to do this:

  • f(x) = cosx;  d(fx)/dx = f'(x) = -sinx
  • f(x) = sinx; d(fx)/dx =f'(x) = cosx
  • f(x) = ex ; d(fx)/dx =f'(x) = ex

Maclaurin Series of cosx

Recall equation (18). 

(18)

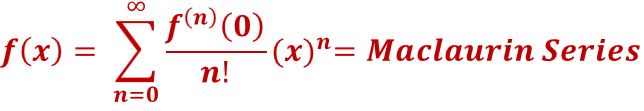
Let’s develop a Maclaurin Series for cosx. 

Compute the first four derivatives of cosx and evaluate at x = 0.

Remember that sin(0) = 0 and cos(0) = 1.  You can derive these from the Unit Circle (see Appendix 3).

  • f(x)   =   cosx; f(0)    =  cos 0 = 1
  • f'(x)  =  -sinx;  f'(0)   = -sin 0 = 0
  • f”(x) =  -cosx;  f”(0)  = -1
  • f”'(x) =   sinx;  f”'(0)  = 0
  • f””(x) =  cosx;  f””(0) = 1

The Maclaurin Series for cosx will be:

Equation (21) 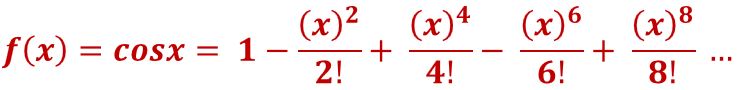 is the Maclaurin Series of cosx

We are going to use this later on in the derivation. Read on!

Maclaurin Series of sinx

Compute the first four derivatives of sinx and evaluate at x = 0.

Remember that sin(0) = 0 and cos(0) = 1.  You can derive these from the Unit Circle (see Appendix 3)

  • f(x)    = sinx;     f(0) = 0
  • f'(x)   = cosx;    f'(0) = 1
  • f”(x)  = -sinx;   f”(0) =0
  • f”'(x)  = -cosx; f”'(0) = -1
  • f””(x) = sinx;   f””(0) = 0

The Maclaurin Series for sinx will be:

Equation (24) 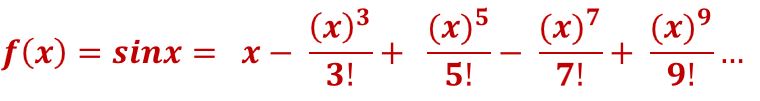 is the Maclaurin Series of sinx

We are going to use this later on in the derivation.

Maclaurin Series of ex

Compute the first four derivatives of ex and evaluate at x = 0.

  • f(x) = ex ; f(0) = 1
  • f'(x) = ex ; f'(0) = 1
  • f”(x) = ex; f”(0) =1
  • f”'(x) =ex; f”'(0) = 1
  • f””(x) =ex; f””(0) = 1

The Maclaurin Series for ex will be:

Equation (26) 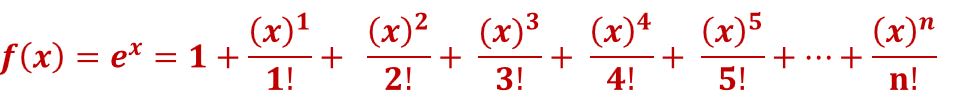 is the Maclaurin Series of ex

Exponential as a Series 1

This is where we slip in the weird number i, the Imaginary Unit, and just accept on faith that this will make more sense later.

So, substitute “ix” into “x” in equation (26).

  • Remember that i (the Imaginary Unit) is . It’s a thing, and allows us to expand our number world into complex numbers. 

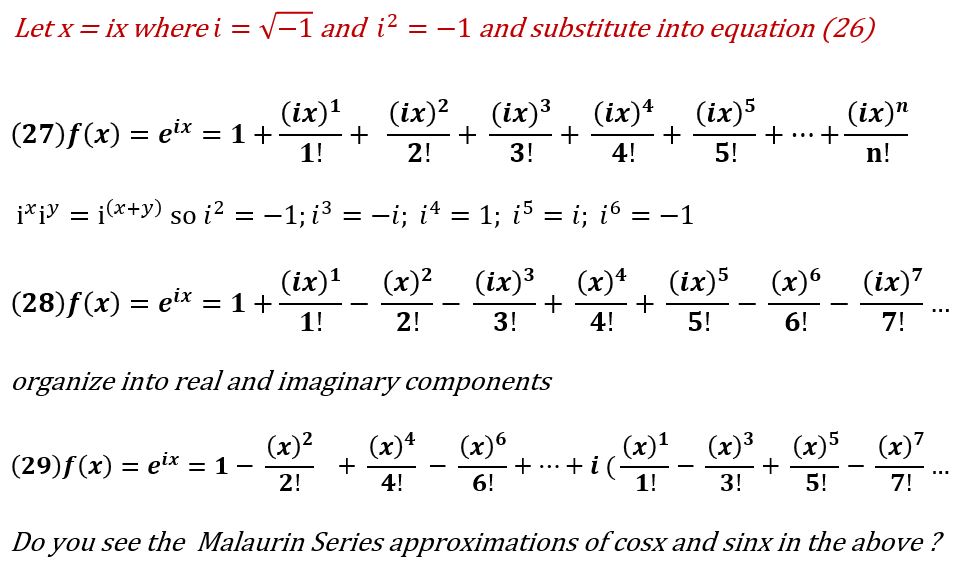
After substituting ix for x in equation (26) and then organizing into real and imaginary components we get equation (29) above.

Equation (29) is the Maclaurin Series approximation for eix .

But we can simplify further because equation (29) contains the Maclaurin series for cosx (equation (21)) and sinx (equation (24)). 

So let’s substitute for these expressions.

The Maclaurin expansion for eix becomes the very famous Euler’s Formula:
 
(30)  = Euler’s Formula where

The Swiss Mathematician Leonhard Euler (pronounced “oiler”) published this in 1748.

Now, Let x= π in Euler′s Formula

Recall that π is the ratio of the circumference of a circle to its diameter = C/D.

(𝟑𝟏) 

but cosπ=−1 and sinπ=0 , so equation (31) becomes

(32) or  f(x) = eiπ =−1  ; Euler’s Identity

So, Euler’s Identity is derived from Euler’s formula when π is substituted for x.

Just about everyone writing or making a video on this on-line will describe Euler’s Identity as the most beautiful equation in math.

I’m pretty sure I’m not as excited as Po Shen Loh at Carnegie Mellon in his video “The Most Beautiful Equation in Math” , but it is cool how such a simple equation can contain so many important functions.

Return to Menu

Summary of the Derivation

Maybe you’ll agree that just doing the math to get to Euler’s Formula and Euler’s Identity (when we put in π for x)  is pretty satisfying in itself.

To recap, we started with the general equation for a Power Series

(4) 

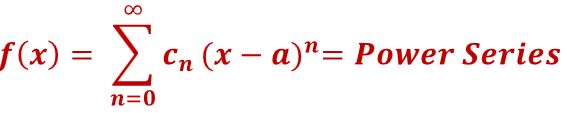
We then found a general expression for the coefficients cn  by

  • taking successively higher derivatives of f(x) and
  • evaluating each of them at a point x = a.

In this way we derived an expression for cn  :

(15) 

so we could express equation (4) as

(16) 
 

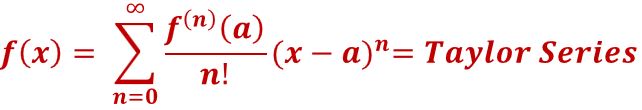
and by assuming that a=0  the Taylor Series became

(18)

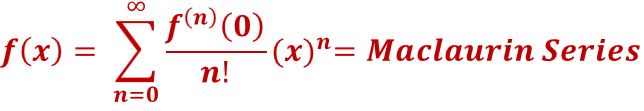
We taught ourselves a little calculus to do all of this but it wasn’t too bad. 

We then applied the Maclaurin Series to cosine x and sine x to produce 

(21) 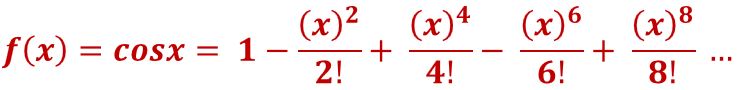; the Maclaurin Series of cosx

(24) 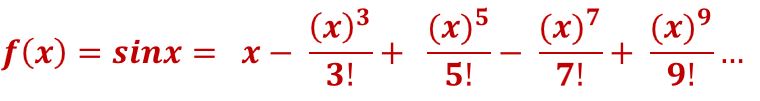; the Maclaurin Series of sinx

and we did the same for ex .

(26) 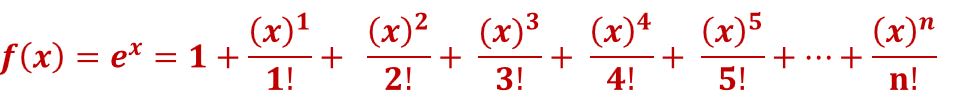; the Maclaurin Series of ex

Then the “shit hit the fan” (well it did for me) when we substituted “x” with “ix” in equation (26) where i is the imaginary number (= ).  

The resulting expression, Euler’s Formula, ended up containing the Maclaurin expressions for both cosx and sinx:

Euler’s Formula
(30)  

And finally, we let x = π such that Euler’s Formula became Euler’s Identity. 

Euler’s Identity

(32) or  f(x) = eiπ =−1  

Like I said, the math by itself is fun to go through, but do these formulas have any meaning or application? 

Well yes, but you need to wrap your brain around i , the Imaginary Unit,  before you can get there. 

Return to Menu

Conclusion

We derived Euler’s Formula and Euler’s Identity with a little bit of Algebra, Trigonometry, and Calculus.

Euler’s Formula

For any real number x (in Radians),

 

Euler’s Identity

Apart from their sheer mathematical elegance, these formulas have much to do with periodic and circular motion.

Because so much of nature has these characteristics, Euler’s formula becomes a very useful tool in modelling natural phenomena and is frequently used in science and engineering fields. 

But to begin to understand , you need to have a basic understanding of complex numbers (see my Posts on the Imaginary Unit and Complex Numbers). 

Return to Menu

Appendix 1 – Graphical Meaning of (x-a) versus x

Return to Taylor Series Derivation Section

Return to Menu 

Appendix 2 – Full Derivation of Taylor and Maclaurin Power Series

Return to Taylor Series Derivation Section

Return to Menu

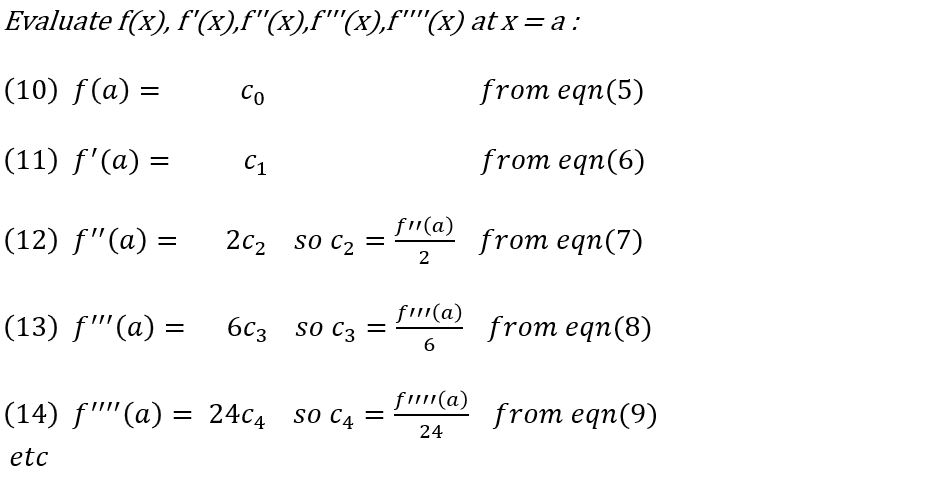
Appendix 3 – Unit Circle and Definition of Sin(0) and Cos(0)

We can derive the definitions of sin(0) and cos(0) by looking at the unit circle and a right triangle drawn into it. 

Picture_Unit Circle

Unit Circle

SOH_CAH_TOA

Did you ever learn the trigonometry mnemonic SOHCAHTOA. It’s an easy way to remember the definitions of sine, cosine, and tangent:

In a right triangle, the sine, cosine and tangent are defined as. 

  • SOH = sine = (Length of Opposite Side)/(Length of Hypotenuse)
  • CAH = cosine = (Length of Adjacent Side)/(Length of Hypotenuse)
  • TOA = tangent = (Length of Opposite Side)/(Length of Adjacent Side)

Deriving cos(0) and sine(0) from the Unit Circle

For the Right Triangle in the Unit Circle we know that
sin θ = Opposite/Hypotenuse = b/h = b
cos θ = Adjacent/Hypotenuse = a/h = a

Therefore the point (a,b) = (cos θ , sin θ ).

So, at θ= 0, position of line h (the terminal side of angle θ) intersects circle at (1,0). So,

cos(0) = 1 and
sin(0) = 0

Deriving cos(0) and sine(0) from a Right Triangle in the Unit Circle

We can derive the same result by using the right triangle as well:
Let θ –> 0, then b–> 0, and h–> a

Therefore,

cos(0) = a/h = 1
sin(0) = b/h = 0/h = 0

Unit circle – Khanacademy.org

Return to Euler’s Formula Derivation Section

Return to Menu

Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for  professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.

Leave a Comment

Your email address will not be published. Required fields are marked *