Menu (linked Index)
Number Classifications
Last Update: November 25, 2024
Introduction
Understanding the various number types (classifications) is critical to gaining a deeper contextual clarity and specificity when applying math.
For example, xn is equal to x multiplied by itself n times, but only if the exponent is a Natural Number i.e. {1,2,3,…).
If n is 0 or 1/2 or -2, the formula for the solution is different.
- x0 = 1
- x-n= 1/xn
- x1/n= nth root of x
A few more examples:
- The square root function is only defined for non-negative Real Numbers.
- The equation x2 = -1 has no Real Number solutions but has two Complex Number solutions.
The reader can use the charts provided in this post to understand number types and their relation to each other.
Number types and their hierarchical relationship are plotted on a hierarchical organization chart and on Venn type diagrams.
These formats show how certain number types encompass (or include) other number types.
For example: Natural Numbers are a subset of Whole Numbers which are a subset of Integers which are a subset of Rational Numbers which are a subset of Real Numbers.
The definitions I provide in this post are based on information from the following:
Another useful website for general math knowledge is https://www.mathsisfun.com/
You can learn more about related topics via my other posts listed below:
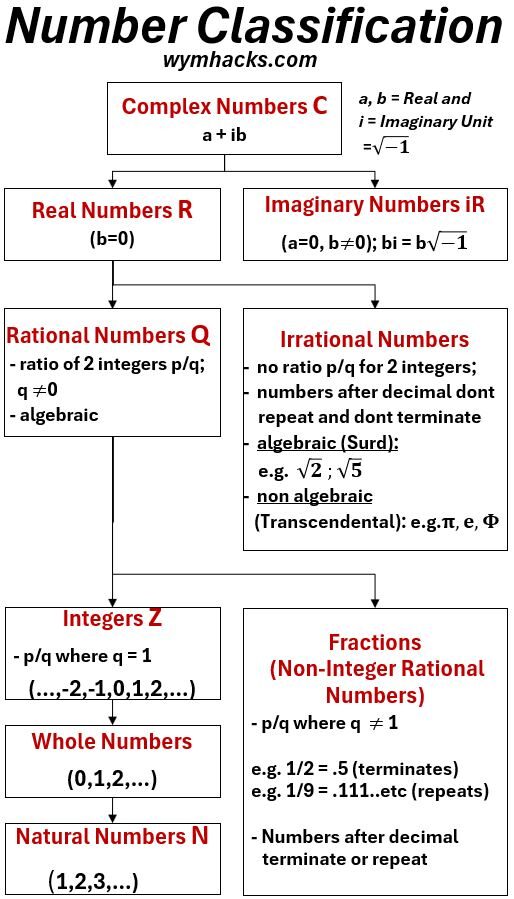
Number Classification Organization Chart
In the chart below, the higher boxes that are “arrow attached” to lower boxes encompass or include those lower boxes i.e. the lower boxes are subsets of the higher boxes.
Notice that Complex Numbers are able to represent all numbers.
Picture_Number Classification Organizational Chart
Number Classification Definitions
- Complex Numbers encompass all other number types.
- Typically denoted as C
- Complex Numbers have a real component a and imaginary component ib where a and b are Real.
- i is the Imaginary Unit = square root (-1) = sqrt(-1) = √(-1)
- Real Numbers Encompass Rational and Irrational Numbers
- Typically denoted as R
- Every Real Number has a corresponding point on the number line.
- The number line extends infinitely in both directions.
- Rational Numbers encompass Integers and Non-Integers
- Rational Numbers can be expressed as a ratio of two integers p/q where q ≠ 0.
- Rational Numbers have a symbol Q (for quotient).
- Rational Numbers are Algebraic.
- An Integer has no fractional part (no numbers after the decimal or no denominator) and is one of the numbers …-2,-1,0,1,2,3…; i.e. p/q where q = 1.
- a Non-Integer Rational Number is any number that has a decimal or fractional part where the numbers after the decimal terminate or repeat. i.e. p/q where q ≠ 1.
- Irrational Numbers cannot be expressed as a ratio of two integers p/q.
- Numbers after the decimal point don’t repeat and don’t terminate
- Can be Algebraic (Surds like sqrt (2) or sqrt (5) )
- Can be non-Algebraic or Transcendental like π (3.14159…), e (2.71828…) , and many others.
- Integers encompass Whole Numbers and Natural Numbers
- Integers are denoted by Z (from the German word Zahl meaning “number”)
- Integers: …,-2,-1,0,1,2,3,…
- Whole Numbers: 0,1,2,3,…
- Natural Numbers are denoted N): 1,2,3,…
Return to Menu
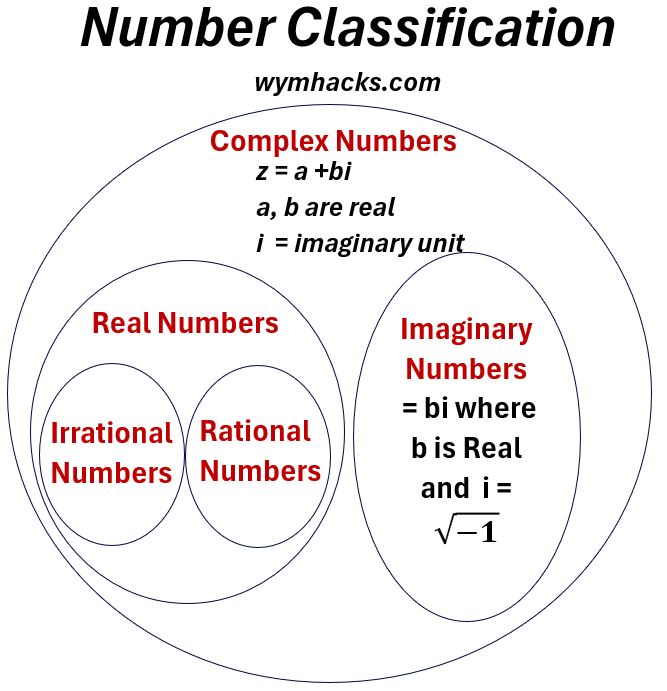
Venn Chart – High Level Number Classifications
Picture_High Level Number Classification Venn Chart
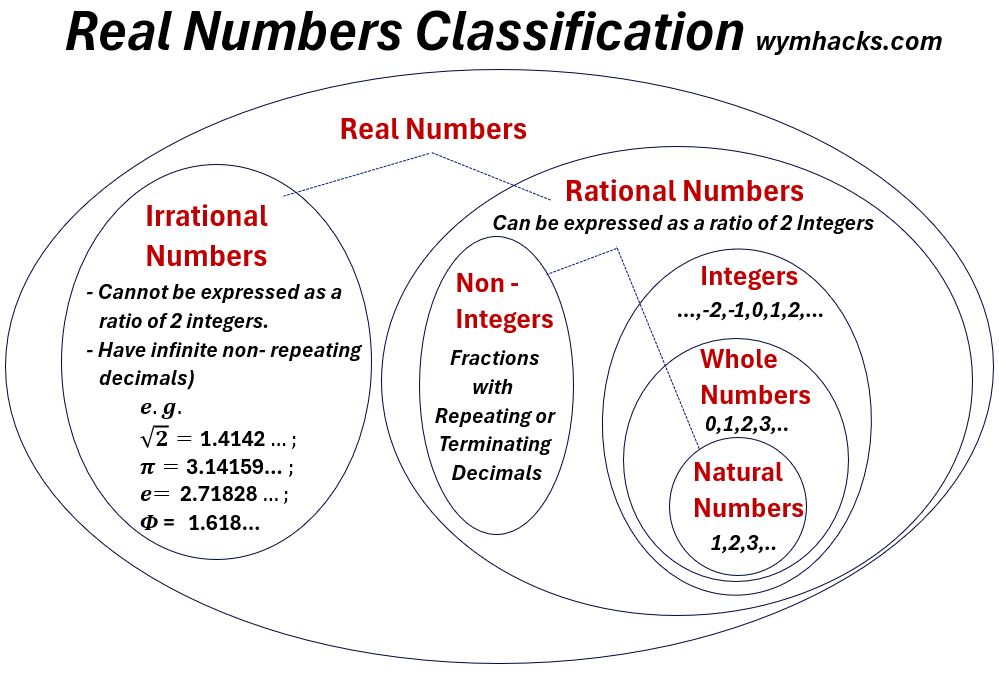
Venn Chart – Real Number Classifications
The chart below is a Venn Chart showing Real Number classifications.
Picture_Real Number Classification Venn Chart
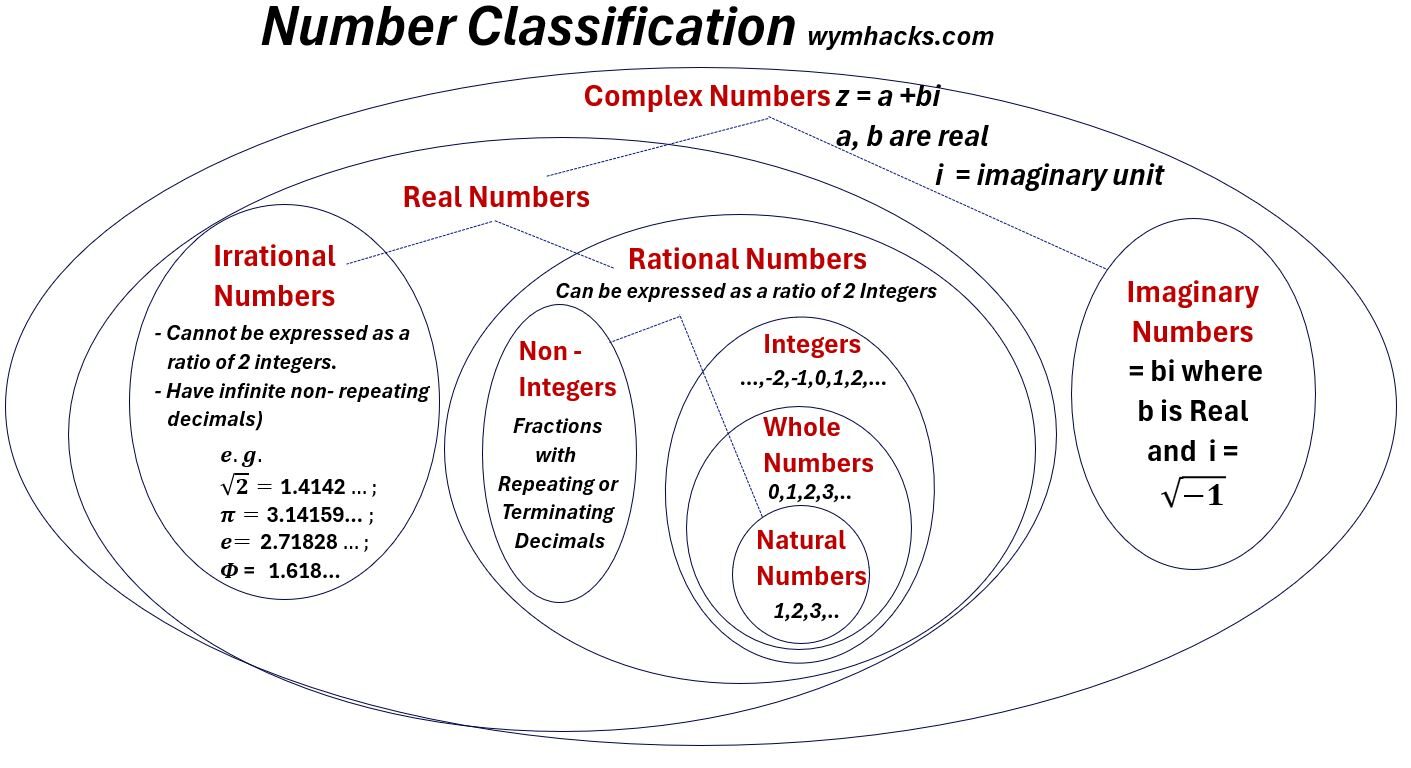
Venn Chart – Detailed Number Classifications
Picture_Full Number Classification Venn Chart
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.