Menu (linked Index)
Complex Number Math
Last Update: December 5, 2024
Introduction
In this post, we’ll see how addition, subtraction , and multiplication of Complex Numbers can be shown geometrically in the Complex Plane.
This will help visualize what is going on with these math operations.
As you read through the examples, remember that Complex Numbers are expressed as z = a + bi on the Complex Plane where
- z = Complex Number = a + bi
- i = Imaginary Unit where by definition i2 = -1 . Or i =

- a = Real Part
- b = Imaginary Part (it’s actually a Real number also)
- bi = Imaginary Number
- Complex Plane = a 2 dimensional (x,y) coordinate system for plotting Complex Numbers where x is Real and y is Imaginary.
You can learn more about Complex Numbers and related topics via my other posts listed below:
Adding Complex Numbers
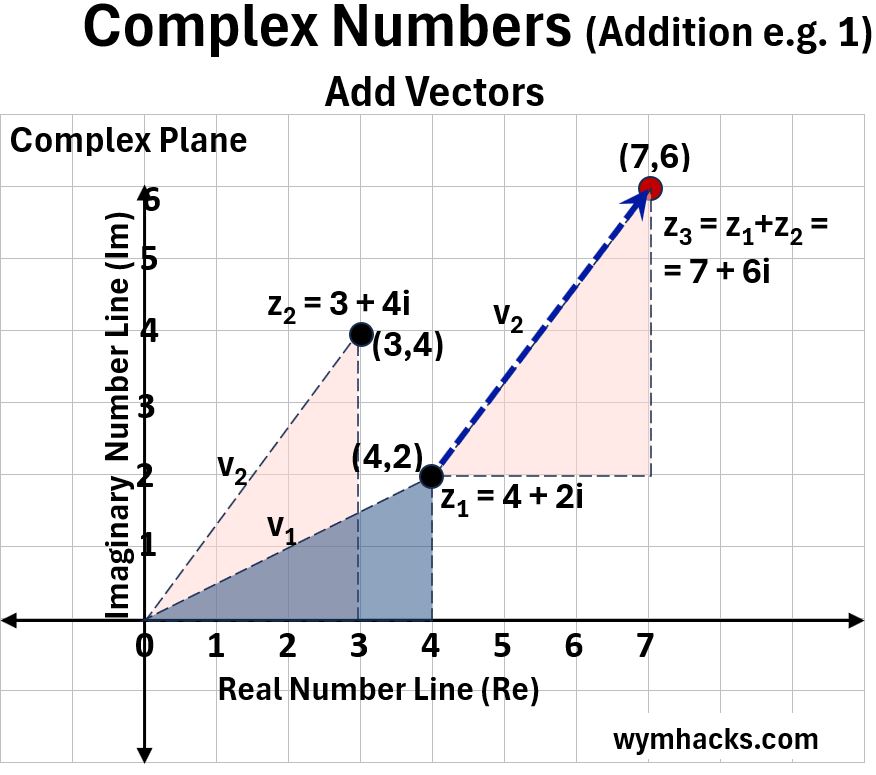
Adding Complex Numbers can be seen as addition of vectors.
In the chart below we are adding (4+2i) to (3+4i).
We can visualize this on the Complex Plane as the addition of the associated right triangles, or more specifically the addition of the Complex Vector v2 to Complex Vector v1.
When adding vectors we always add the “tail” of one to the “tip or arrow side” of the other.
Picture_Complex Number Addition (4+2i) + (3+4i)
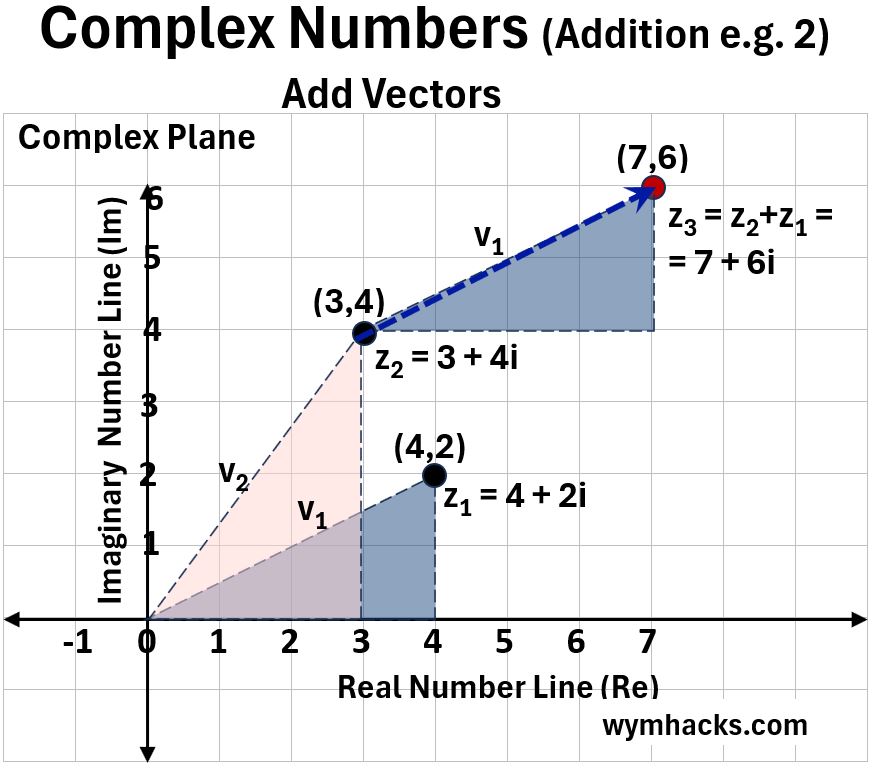
In the chart below we are adding (3+4i) to (4+2i) i.e. the reverse of what we did above.
This time we are adding Complex Vector v1 to v2.
This is the Commutative Law on display. We took different paths but got to the same result at location (7,6).
Picture_Complex Number Addition (3+4i) + (4+2i)
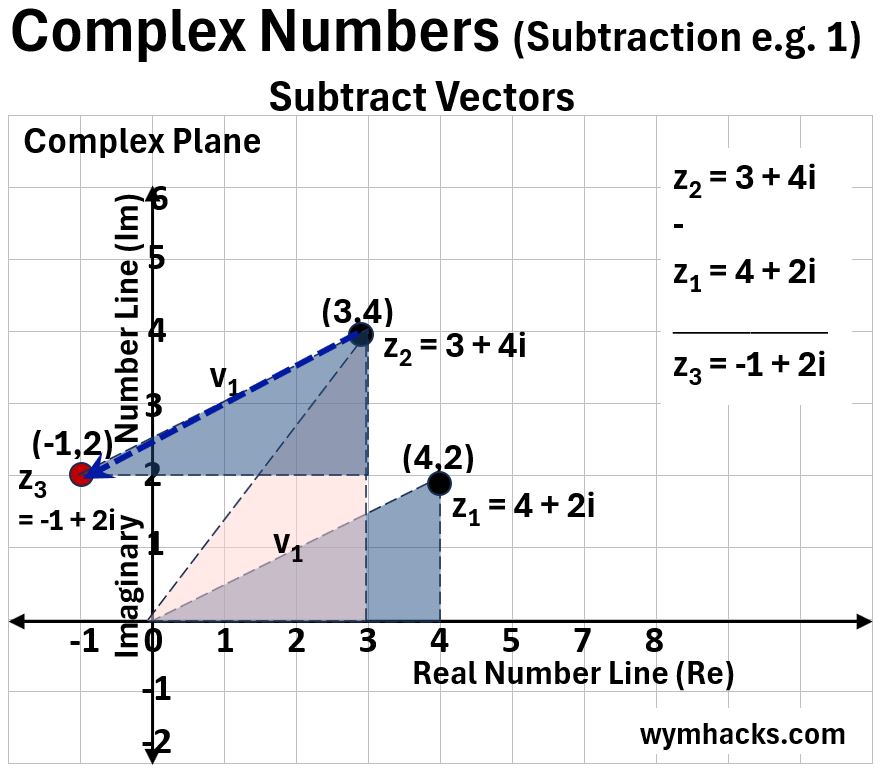
Subtracting Complex Numbers
In the graph below we show how subtracting two Complex Numbers on the Complex Plan can be visualized via right triangles and Complex Vectors.
When subtracting (4+2i) from (3+4i) we are taking Complex Vector v1, flipping the direction of the arrow and adding it to Complex Vector of (3+4i).
When we subtract vectors we flip the tail and tip (arrow) of the subtrahend (the y in x-y) and then add it (tail to tip) to the minuend (the x in x-y).
The resultant Complex Number is (-1 + 2i).
Picture_Complex Number Subtraction (3+4i)-(4+2i)
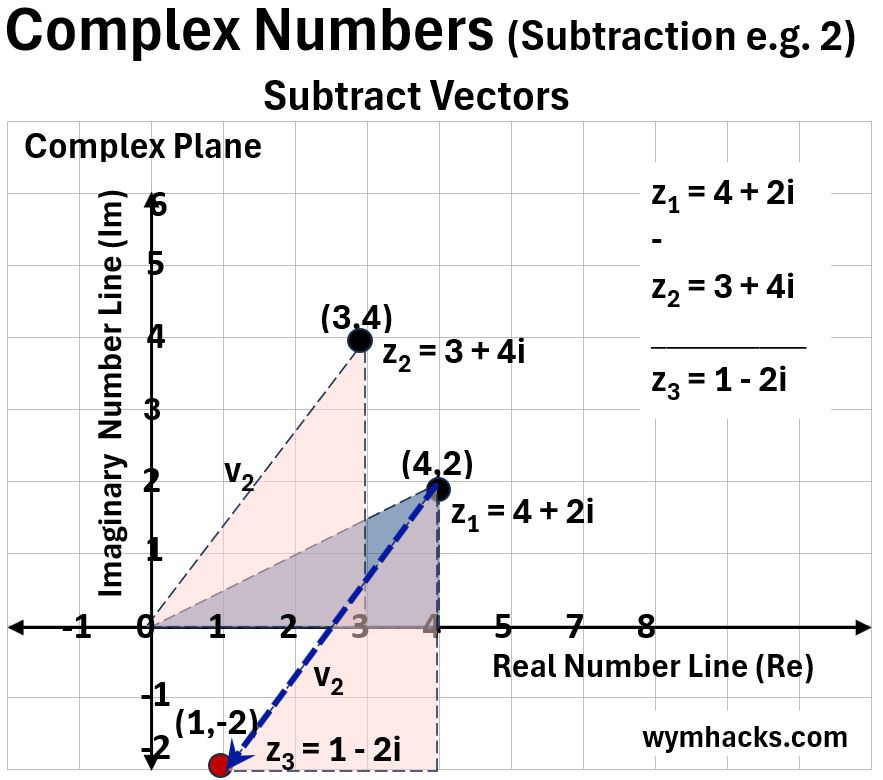
Subtracting these complex numbers the other way will of course give a different number (subtraction is not Commutative).
When subtracting (3+4i) from (4+2i) we are taking Complex Vector v2, flipping the direction of the arrow and adding it to the Complex Vector of (4+2i).
The resultant Complex Number is (1 – 2i).
Picture_Complex Number Subtraction (4+2i)-(3+4i)
Complex Number Multiplication
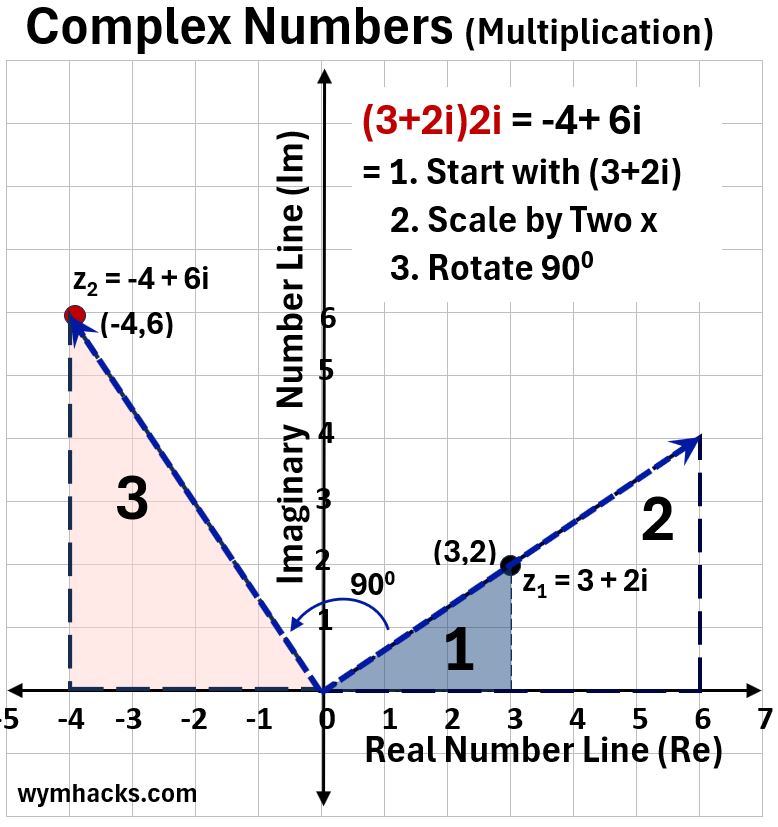
In the graph below we are starting with a Complex Number (3+2i) and multiplying it by 2i.
We can think of this as a two step process where
- (3+2i) is first scaled in size by 2 times (triangle 1 scales to triangle 2) and then
- triangle 2 (or the Complex Vector or Hypotenuse of triangle 2) is rotated 90 degrees from the positive Real Axis.
The final triangle 3 contains the result of (-4+6i)
To understand the second “rotation step” you have to remember that multiplying a Complex Number by i rotates it 90 degrees counterclockwise (see my post on Complex Numbers).
Picture_Complex Multiplication (3+2i)2i
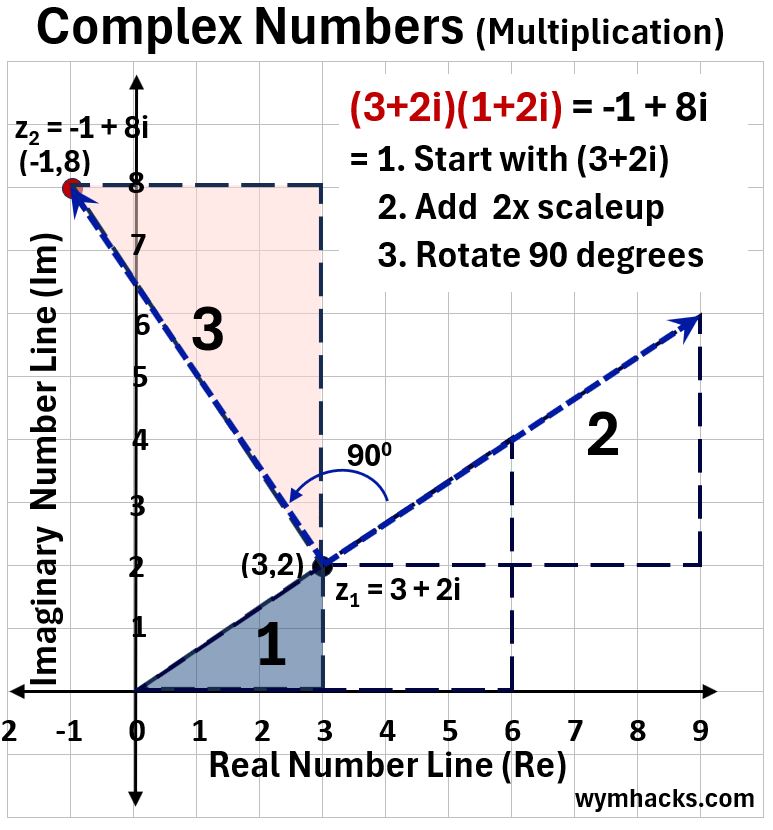
Now, lets take (3+2i) and multiply it by (1+2i) as shown in the graph below.
Starting with triangle 1 for (3+2i) we
- Scale it up by 2x AND add it to (3+2i) to end up with triangle 2.
- Triangle 2 is then rotated 90 degrees to arrive at the result (-1+8i).
You could also multiply the terms out (using FOIL..First, Outside, Inside, Last method) and then add each number (starting at (0,0)) to get to the result
- (3+2i)(1+2i) = 3 + 6i + 2i -4 so from (0,0)
- Go right 3, up 6i, up 2i, and then left 4 to get to
- (-1+8i)
Picture_Complex Number Multiplication (3+2i)(1+2i)
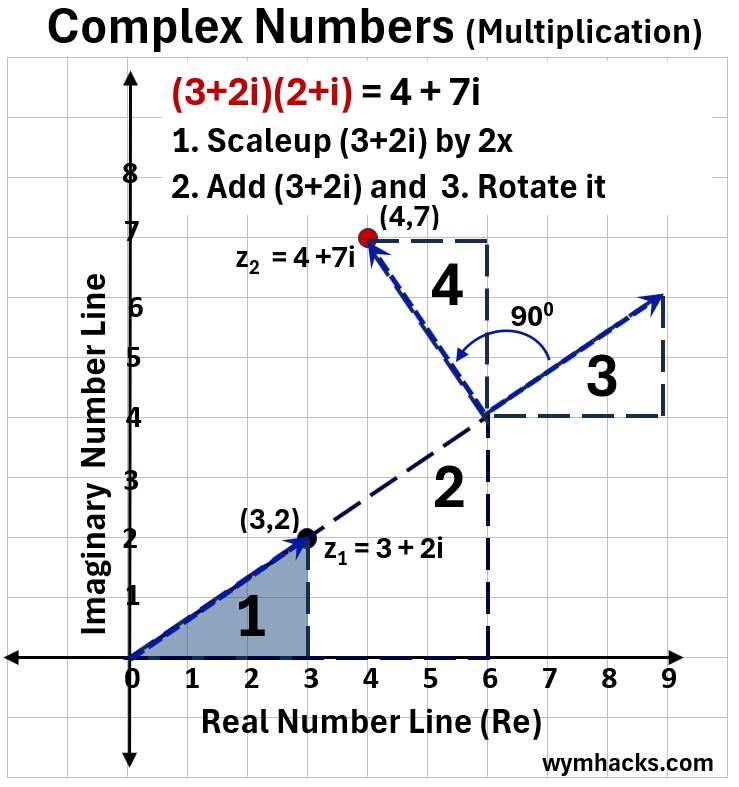
Let’s do one more. Multiply (3+2i)(2+i) as shown in the graph below.
Method 1:
- Scale up triangle (3+2i) by 2x to give triangle 2
- Add triangle 1 to it (becomes triangle 3)
- Flip triangle 3 90 degrees counterclockwise to get to the result (4+7i)
Picture_Complex Number Multiplication (3+2i)(2+i) – Triangle Method
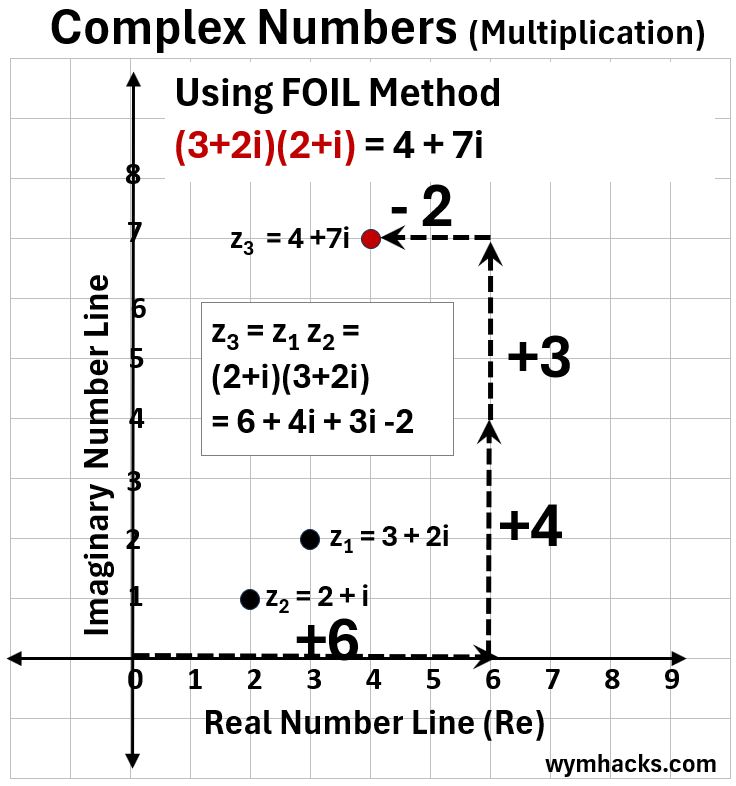
In the graph below we solve the same problem using the FOIL method to produce the different number (steps) to navigate from (0,0) to the answer.
- (3+2i)(2+i) = 6 + 3i + 4i -2. So starting from (0,0)
- Go right 6, up 3i, up 4i, left 2 to get to the result (4+7i)
Picture_Complex Number Multiplication (3+2i)(2+i) – FOIL Method
Complex Numbers Can Simplify The Math
- Using Euler’s Formula, we can express a complex number z = a + bi in polar form (see my post Complex Numbers) as
- z = reiθ = r(cosθ + i sinθ) where
- e (Euler’s number): An irrational mathematical constant approximately equal to 2.71828…
- i (imaginary unit): The square root of negative one =

- θ (angle in Radians): Represents any real number angle in Radians (2π Radians = 360 degrees ; 1 Radian = ~57.3 degrees)
- r = the modulus (vector from (0,0) to the complex number in the Complex Plane; It’s the hypotenuse of the right triangle formed)
- This equation allows for the transformation of trigonometric expressions into simpler exponential forms.
- In exponential format, multiplication and division are simplified to addition and subtraction
- example 1: z1z2 = r1eiθ1r2eiθ2 = r1 r2 ei(θ1+θ2)
- example 2: z1/z2 = r1/r2 ei(θ1-θ2)
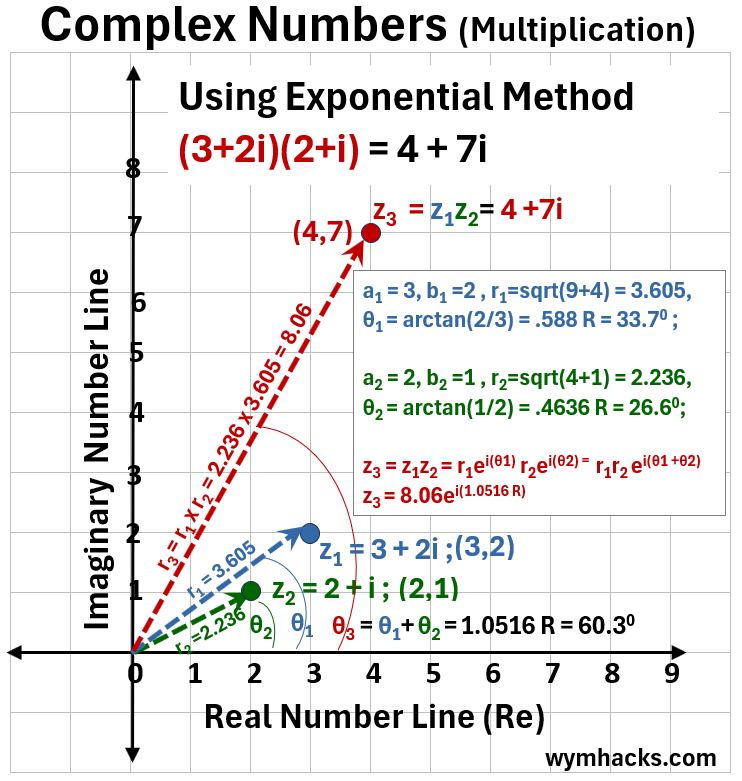
In the graph below, we solve (3+2i)(2+i) again using the polar exponential form of a complex number (z = eiθ).
This is not a graphical method per se but the results are displayed nicely on a graph.
Picture_Complex Number Multiplication (3+2i)(2+i) – Exponent Method
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.