Menu (linked Index)
Unit Circle and Definitions of Radian and π
Last Update: October 16, 2025
Introduction
In this post we’ll review some of the important mathematical formulas and properties derived from the circle.
You probably know that
- the constant pi = π = 3.14159..
- there are 360 degrees (3600) in a circle.
- a Radian is another way to express an angle and equals about 57.30 (did you know that?).
- you can derive useful trigonometric functions from a circle (did you know that?).
But, to be certain, let’s review them and develop some meaning behind them.
You can learn more about related topics via my other posts listed below:
Properties of Circle
I’ve drawn a circle below. Let’s review some of its basic properties.
Picture_Unit Circle
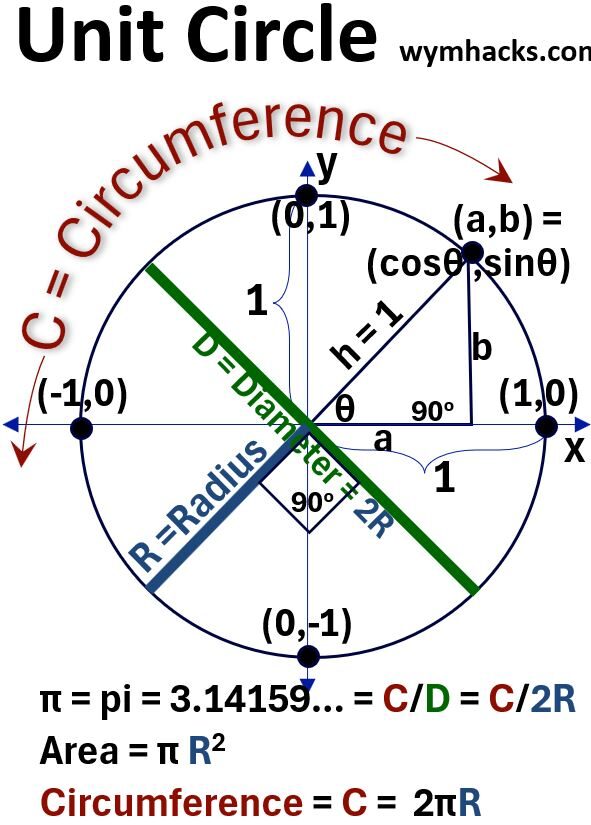
Circle Geometry
I’ll repeat in words below what the drawing above is telling you.
- The Diameter D of a circle is a straight line segment that passes through the center of the circle and connects two points on the circle’s edge.
- The Radius R of a circle = D/2
- The Circumference of a circle = C = 2πR
- The Area of a circle = A = π R²
- Pi (π) is a mathematical constant that represents the ratio of a circle’s Circumference to its Diameter.
- Pi (π) = C/D
- Pi (π) is approximately (~) equal to 3.14159.
- π is an irrational number, meaning its decimal patterns don’t repeat.
- π is a transcendental number i.e. it cannot be expressed as a finite combination of integers, roots, and basic arithmetic operations.
- A degree is a unit of measurement for angles.
- An angle is formed by lines that share a common endpoint.
- It quantifies how much one line deviates from another.
- A quarter of a rotation around a circle is 90 degrees or 900 (called a right angle).
-
A half a rotation around a circle is 1800
- A complete rotation around a circle is 3600
Right Triangle Trigonometry
In the picture above, I drew a right triangle, whose hypotenuse h is drawn from the center of the circle to the boundary.
We’ll assume that the circle has a radius of 1 so h = 1.
The sine, cosine, and tangent of the angle θ are defined as follows (remember the mnemonic SOH-CAH-TOA)
- sin θ= Opposite/Hypotenuse = b/h = b
- cos θ = Adjacent/Hypotenuse = a/h = a
Therefore the point (a,b) = (cos θ , sin θ ).
At θ = 0, the position of line h (the terminal side of angle θ) intersects the circle at (1,0). So,
- cos 0 = 1 and
- sin 0 = 0
We can derive the same result by using the right triangle as well:
Let θ –> 0, then b–> 0, and h–> a, Therefore
- cos 0 = a/h = 1
- sin 0 = b/h = 0/h = 0
Unit Circle Trigonometry
In the last section , we saw that,
- Using the unit circle,
- with angle θ defined as 0 for the x axis line that intersects the unit circle at (1,0)
- and where θ increases counterclockwise all the way around the circle back to 0 degrees.
We can use a right triangle in the first quadrant of the unit circle to establish more broad definitions for the trigonometric functions.
Unit Circle Trigonometry – For All Four Quadrants
The definition of sine and cosine on the unit circle is consistent across all four quadrants of a cartesian plane:
- cos θ is the x-coordinate of the point on the circle.
- sin θ is the y-coordinate of the point on the circle.
While you use a right triangle for the first quadrant, the key to the other quadrants is understanding
-
- symmetry and the reference angle θR
to determine the magnitude of the value, and
- the coordinate system
to determine the sign of the value.
Unit Circle Trigonometry – Sign of (x,y) Values
The unit circle is overlaid on the Cartesian coordinate plane, which dictates the sign of the x and y coordinates in each quadrant.
Since cos θ = x and sin θ = y, the signs of x and y directly determine the signs of the functions.
Unit Circle Trigonometry – Magnitude (x,y) Values
Refer to the drawing below.
Picture: Unit Circle with Right Triangles in Each Quadrant
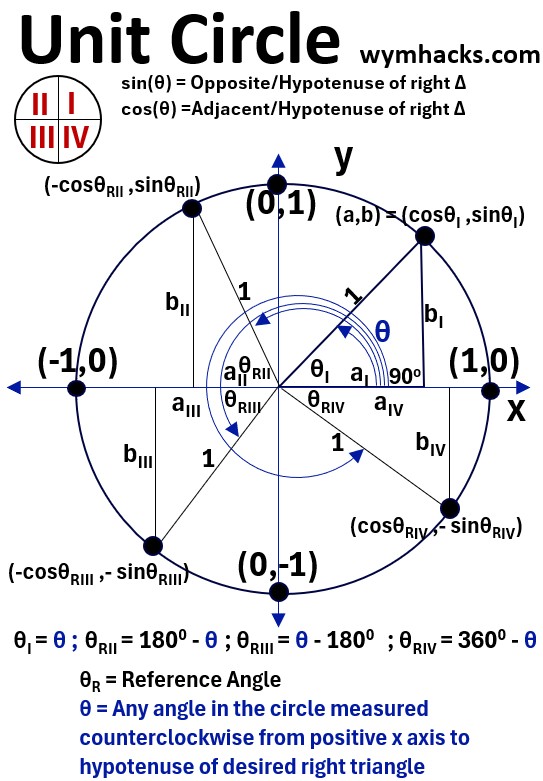
For any angle θ, starting at the positive x axis and extending in Quadrants I, II, III, or IV, you can create a corresponding right triangle.
This triangle is formed by the terminal side of θ , the x-axis, and a vertical line from the point on the circle to the x-axis.
The reference angle θRII or RIII or RIV is the positive acute angle between the terminal side of θ and the closest part of the x-axis.
- θI = θ ; Quadrant 1 Angle
- θRII = 1800 – θ ; Quadrant 2 Reference Angle
- θRII = 0 – 1800 ; Quadrant 2 Reference Angle
- θRII = 3600 – θ ; Quadrant 2 Reference Angle
The trigonometric value (magnitude only) for any angle θ is the same as the value for its reference angle θ , which is always in Quadrant I.
So, we can now define the trigonometric functions for all angles (i.e. we are not confined to right triangles where θ must be >0 degrees and < 90 degrees).
In the picture below, I show the (cosine, sine) values for select points all around the unit circle.
Notice that the values in quadrants II, III, and IV have the same magnitudes as the values in Quadrant I.
Picture: Unit Circle With Trigonometric Values
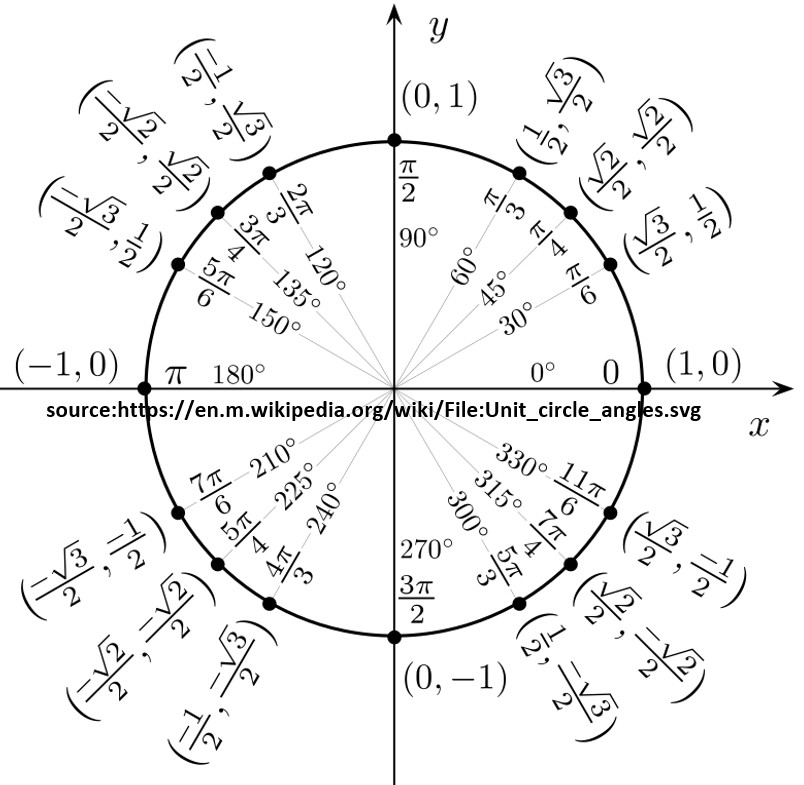
In the diagram above, the angle values π/6, π/4, π/3, π/2, 2 π/3 etc. are in Radians where 2π Radians = 3600 degrees.
We’ll discuss Radians in more detail in the following section.
- 0 Radians; cos (00 ) = 1; sin (00) = 0
- π/6 Radians; cos (300 ) = sqrt(3)/2; sin (300) = 1/2
- π/4 Radians; cos (450 ) =sqrt(2)/2; sin (450) = sqrt(2)/2
- π/3 Radians; cos (600 ) = 1/2; sin (600) = sqrt(3)/2
- π/2 Radians; cos (900 ) = 0; sin (900) = 1
- 2π/3 Radians; cos (1200 ) = -1/2; sin (1200) = sqrt(3)/2
- 3π/4 Radians; cos (1350 ) = -sqrt(2)/2; sin (1350) = sqrt(2)/2
- 5π/6 Radians; cos (1500 ) = -sqrt(3)/2; sin (1500) = 1/2
- π Radians; cos (1800 ) = -1; sin (1800) = 0
- 7π/6 Radians; cos (2100 ) = -sqrt(3)/2; sin (2100) = -1/2
- 5π/4 Radians; cos (2250 ) = -sqrt(2)/2; sin (2250) = -sqrt(2)/2
- 4π/3 Radians; cos (2400 ) = -1/2; sin (2400) = -sqrt(3)/2
- 3π/2 Radians; cos (2700 ) = 0; sin (2700) = -1
- 5π/3 Radians; cos (3000 ) = 1/2; sin (3000) = -sqrt(3)/2
- 7π/4 Radians; cos (3150 ) = sqrt(2)/2; sin (3150) = -sqrt(2)/2
- 11π/6 Radians; cos (3300 ) = sqrt(3)/2; sin (3300) = -1/2
- 2π Radians; cos (3600 ) = 1; sin (3600) = 0
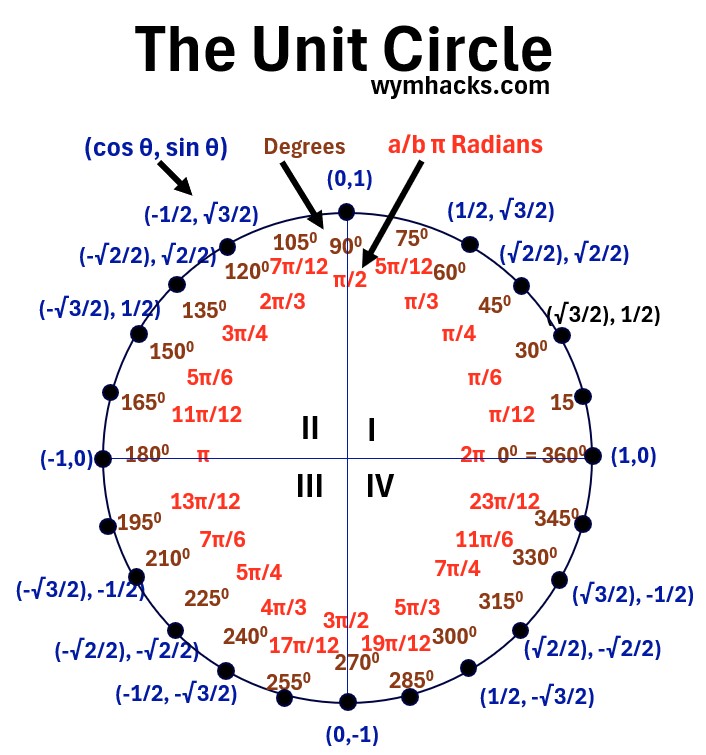
The Unit Circle and The Radian
Consider the Unit Circle in the picture below.
It has a Radius of 1, and when this Radius rotates (counterclockwise by convention from the positive horizontal axis), the angle θ goes from 00 to 3600.
Picture_Unit Circle with Radian and Degree Designations
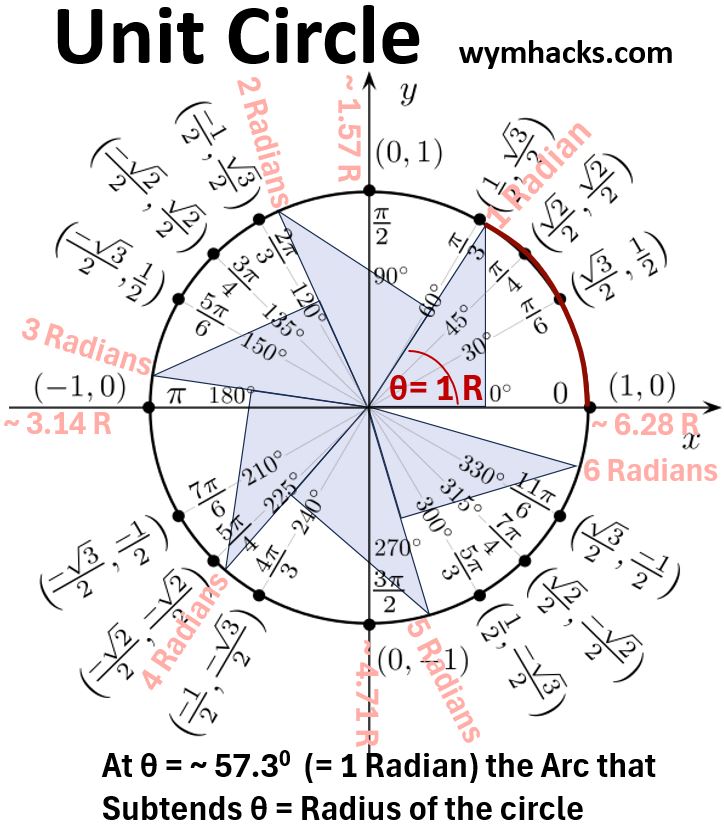
The Radian as an Angle Measure
If we
- start the radius in the positive horizontal position and
- move it counterclockwise until θ = 1 Radian, then
- the length of the arc that subtends θ will equal the length of the radius
In fact, the definition of a Radian is the ratio of the arc length to the radius of a circle.
Subtend means to be opposite to and extend from one side to the other of something.
- For example, in the Unit Circle above, the circle arc from point (1,0) to point (sqrt(3)/2 , 1/2) subtends the angle of 300
Moving from the horizontal positive radius line of the Unit Circle in a counterclockwise direction:
- θ = 300 = π/6 Radians = π/6 R
- θ = 450 = π/4 R = ~ .785 R
- θ = ~ 57.30 = 1 Radian
- θ = 600= π/3 R = ~ 1.05 R
- θ = 900 = π/2 R
- θ = 1800 = π R
- θ = 2700 = 3π/2 R
- θ = 3600 = 2πR
To get a better visual understanding of the Radian, take a look at the shaded right triangles drawn into the Unit Circle in the picture above.
In these “Radian Triangles” the hypotenuses extend to the circle and mark the radius of angle R:
- If we start with the triangle with θ = ~ 57.30
- and rotate it counterclockwise by an additional θ,
- we can fit 6 full triangles before we get to 3600
- The remaining gap to 360 is therefore ~.28 R.
- So it takes ~6.28 triangles = ~6.28 θ= ~6.28 R to rotate one time around the circle.
- ~6.28R = ~(2)(3.14159)R = 2πR
Radians Are A Fundamental Angle Measure
Radians are directly connected to the geometry of a circle and so are a more fundamental measure of an angle than degrees.
- Degrees are arbitrarily divided into 360 parts.
- A Radian is defined as the ratio of the arc length to the radius of a circle.
- So it is directly related to the properties of a circle.
- The Radian is independent of any specific unit of length i.e. it is dimensionless.
- Radians simplify many mathematical formulas and calculations, particularly in calculus and trigonometry.
- The derivatives of trigonometric functions are much simpler when expressed in radians.
- For example d/dx (cosx) = – sinx is only true if x is measured in Radians (you will get the wrong answer if you assume degrees)
- For example d/dx (sinx) = cosx is only true if x is measured in Radians (you will get the wrong answer if you assume degrees)
Excellent References
Conclusion
Here is a summary of the definitions and properties related to circles.
- The Radius R of a circle = Diameter/2
- The Circumference of a circle = C = 2πR
- The Area of a circle = A = π R²
- Pi (π) = C/D = Pi (π) is approximately (~) equal to 3.14159.
- π is an irrational number, meaning its decimal patterns don’t repeat.
- π is a transcendental number i.e. it cannot be expressed as a finite combination of integers, roots, and basic arithmetic operations.
- A quarter of a rotation around a circle is 90 degrees or 900 (called a right angle).
- The unit circle provides the basis for a more broad definition of the trigonometric functions
- not constrained to the angles of a right triangle (<90 and >0)
- cos, sin, tan, etc. are defined for θ = 0 – 360
- A Radian is the ratio of the arc length to the radius of a circle = (circle arc length)/(circle radius)
- For θ = 1 Radian, the length of the arc that subtends θ will equal the length of the radius.
- 1 Radian = ~ 57.30
- θ = 900 = π/2 R
- θ = 1800 = π R
- θ = 2700 = 3π/2 R
- θ = 3600 = 2πR
- Radians are directly connected to the geometry of a circle and so are a more fundamental measure of an angle than degrees.
- Standard definitions of derivatives of Trigonometric Functions assume angles are in units of Radians.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.