Menu (linked Index)
AC Voltage and Current Equations
Last Update: November 29, 2025
Introduction
A three-phase power generator creates electricity by
- rotating a powerful magnet (the rotor)
- inside a stationary frame containing three separate sets of wire coils (the stator),
- each spaced 120 degrees apart .
Picture: Simplified Three Phase AC Generator
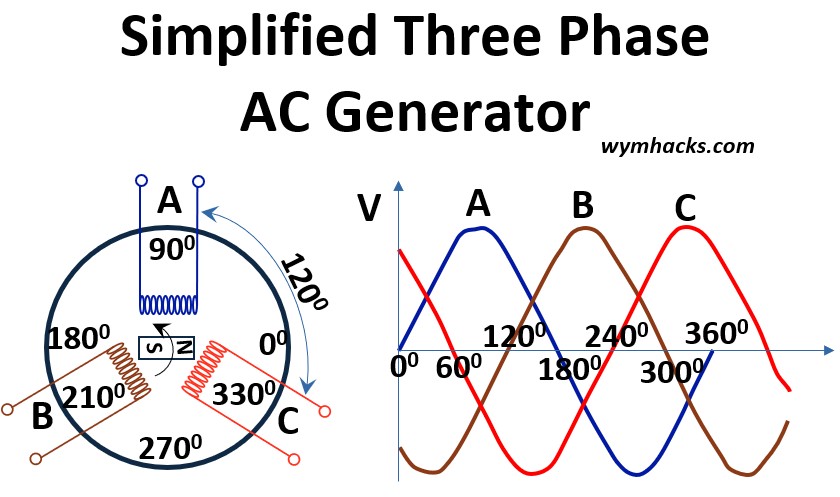
As the magnet spins, its magnetic field sweeps across the coils, inducing a voltage in each one, a principle known as electromagnetic induction.
Because the coils are physically spaced 120 degrees apart, the voltage waveform produced in each coil is also out of phase by 120 degrees from the others.
This process simultaneously generates three distinct AC voltages of the same frequency and amplitude, which are then transmitted to produce the highly efficient and constant power delivery characteristic of three-phase power .
To fully understand the precise relationship between the spinning magnet and the generated electricity, this article derives the mathematical equation that formally defines the periodic, sinusoidal shape of each of these three voltage waveforms.
This equation is essential for modeling and analyzing all aspects of AC power generation.
Faraday’s Law and Magnetic Flux
Faraday’s Law
According to Faraday’s Law of Induction, the induced EMF ( or ) in a coil is proportional to the rate of change of magnetic flux () through the coil:
- is the number of turns in the coil.
Magnetic Flux
The magnetic flux through a single loop of area in a uniform magnetic field is given by:
(2) ΦB = Magnetic Flux = (B)(Ap) =BAcos(θ) = B̄•Ā ; for Uniform B and Flat Surface where
- ΦB = magnetic Flux (units: (N/C)m2)
- Ap (units: m2) = Perpendicular component of A that the magnetic field passes through.
- B = The magnetic field (units: N/C)
- B̄•Ā = dot product of the magnetic field vector and the area vector.
- θ = angle between area vector and B vector
Derivation Model: Rotating Coil
I mainly used this excellent video to write this section:
While large-scale generators typically use a rotating magnetic field within stationary coils, a simpler conceptual model—a rotating coil within a constant magnetic field—results in the exact same sinusoidal equations for the induced voltage and current.
To simplify the mathematical derivation, we will utilize this equivalent model.
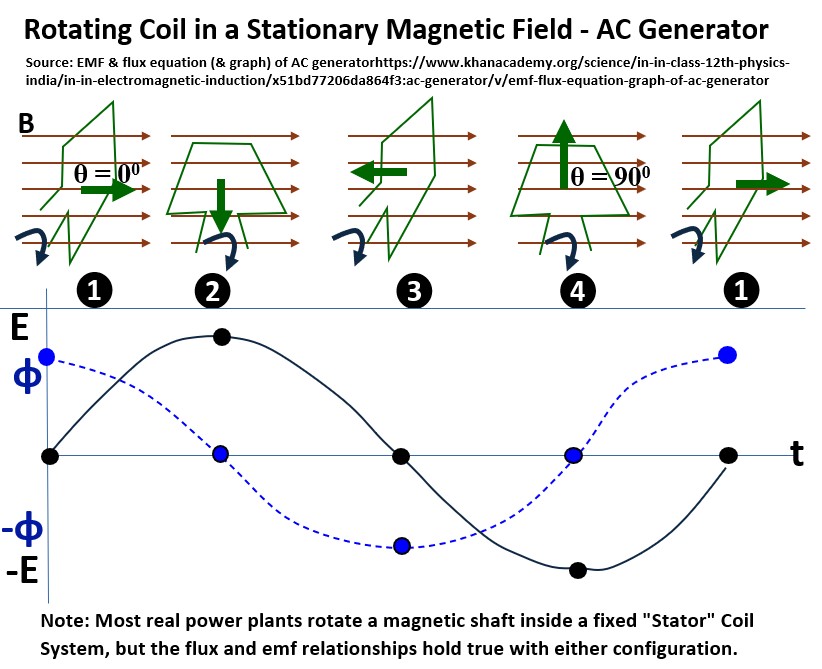
We’ll use the simplified rotating coil concept depicted in the picture below to derive our sinusoidal equation.
Picture: Rotating Coil in a Stationary Magnetic Field (AC Generator; Alternator)
- A coil is being rotated in a constant magnetic field B where
- θ = is the angle between B and
- the Area Vector (the green arrow situated perpendicular to the flat surface of the coil) .
- A plot of Magnetic flux Φ and EMF (E or Voltage) vs time is generated with each 90 degree rotation of the coil.
Voltage Equation Derivation
The coil in the model rotates at a constant angular velocity (in radians per second) so we can let
where the rotational angle is represented as a function of a time term and an initial angle ɸ .
- ω = 2πf is the angular frequency (in radians/second), where f is the frequency in Hertz.
- t is the time (in seconds).
- ɸ is the initial phase angle
Derivation of the Sine Form of the AC Voltage Equation
If the coil starts at ) with its area parallel to the magnetic field, the angle between the area vector and the magnetic field at any time is:
Substituting this into the flux equation (2) gives:
(4) Φ(t) = BAcos(ωt)
Now, substitute equation (4) into Faraday’s Law (equation 1) for a coil of turns:
- See my post The Derivative to see how to use the chain rule for d/dt(cos())
Derivation of the Cosine Form of the AC Voltage Equation
This time, let’s start the coil in position 4 (❹, in the picture above) with its area vector perpendicular to the magnetic field, the angle between the area vector and the magnetic field at any time is:
Substituting this into the flux equation (equation 2) we get:
- cos(θ + π/2) = -sin(θ) ; Geometry and Trigonometry Rules)
Now, substitute (12) into Faraday’s Law for a coil of turns (equation 1):
- See my post The Derivative to see how to use the chain rule for d/dt(sin())
Substituting this into (16) gives
Summary: Mathematical Expressions for AC Voltage
General Forms of Voltage Equation
The general forms of the alternating current voltage equation are:
(19) V(t) = Vcos(ωt+ϕ)
(20) V(t) = Vsin(ωt+ϕ)
Where:
- is the peak voltage (amplitude).
- is the angular frequency (in radians/second), where is the frequency in Hertz.
- is the time (in seconds).
- is the initial phase angle (or just phase angle), which accounts for the starting position of the coil or a time shift relative to a reference.
Preferred Form In Electrical Engineering
The cosine form for voltage (and current) is the standard in electrical engineering because it let’s us use phasor analysis.
This method:
- Converts the hard calculus (derivatives and integrals) in AC circuits into simple algebra (multiplication and division).
- The math convention requires us to take the “real part” of the complex number used in this method.
- Because of Euler’s identity, the real part is mathematically equal to the cosine function.
So, using the cosine form makes the complex math much easier and is the established rule.
Or explained a bit more simply:
We use the cosine version of the voltage equation because it is the real part of the complex exponential used in AC circuit analysis.
In math, Euler’s formula links the two:
- Read my blog to learn more: Exploring Euler’s Formula
- Euler’s Formula: e= cos(θ) + jsin(θ) where j = sqrt(-1)
Electrical engineers agree to use the real part (the cosine term) as the standard way to convert the complex analysis back into the actual, measurable voltage or current.
The above still probably wont make much sense to you unless you dig into how electrical engineers do frequency domain analysis.
Go to my blog to learn more about this.
- AC Circuit Basics: i-v Relationships, Impedance, and Admittance
- Read the section titled “Pure Inductor and Capacitor Impedance – Frequency Domain Analysis”
Current Equation Derivation
The equation for instantaneous current, follows from applying the instantaneous voltage to an electric circuit, typically using Ohm’s Law or circuit laws.
Simple Resistive Circuit (Ohm’s Law)
For a simple circuit with a purely resistive load , Ohm’s Law is applied instantaneously:
Substituting in the cosine form of the voltage equation (eq. 20), equation 21 becomes:
(22) V = IR = Vcos(ωt+ϕ)
Defining , we get the current equation:
Starting with the sine form of the voltage equation we can derive the sine form of the current equation
General AC Circuit (Impedance and Phase Shift)
In circuits with capacitors () and/or inductors (), the relationship is more complex:
- The ratio of to is called the Impedance (), which is the total opposition to current flow.
- Thus,
- The current waveform will have a different phase angle () than the voltage () due to the properties of and . This is the phase shift ().
Summary
The general forms for AC voltage,
V(t) = Vcos(ωt+ϕ) or V(t) = Vsin(ωt+ϕ)
and current,
or
are derived from the principle of electromagnetic induction.
AC voltage is generated by a rotating coil in a magnetic field, where Faraday’s Law, and the sinusoidal nature of the magnetic flux , α cos(θ) , lead directly to the dependency, where
- Vis the peak voltage and
- Iis the peak current.
- omega is the angular frequency.
- t is time.
is the initial phase angle (or just phase angle),
- which accounts for the starting position of the coil or a time shift relative to a reference.
The AC voltage expression is obtained by solving Faraday’s law using the and cos(θ) relationship.
The AC current expression is obtained by
- applying Ohm’s Law (I = V/R),
- substituting the voltage expression and
- defining I = V/R,
confirming that both quantities vary sinusoidally and share the same frequency.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
