Menu (linked Index)
Euler’s Number
Last Update: December 11, 2024
Introduction
In this article we’ll describe and define Euler’s constant e, which is a non terminating, non repeating number equal to 2.718281828459045…
It is an indicator of continual growth and is used widely in science to describe natural phenomenon.
So, I think it’s worth your time to learn a little about it.
You can learn more about related topics via my other posts listed below:
What is e?
Euler’s Number e is a constant that equals 2.718281828459045…keeps going.
e = 2.718281828459045… Euler’s Number
e has the following characteristics:
- e numbers after the decimal place don’t terminate
- e numbers after the decimal place don’t end with a repeating sequence
- e is the Base of Natural Logarithms i.e. loge(x) = ln(x).
- e is Irrational (can’t be expressed as the ratio of two integers).
- e is Transcendental (not Algebraic meaning not root of any integer polynomial).
So in terms of the Number Classification System, e is a constant that is Real, Irrational, and Transcendental.
Before delving into a some of the mathematical properties of e, let’s get a feel for its history and some of the key people who discovered and developed it.
e History Outline
note: I use the term “mathematical concept e” below to make the point that the term “e” was not being used formally before the 1720s.
1618 – Scotland
John Napier and William Oughtred publish a book on Logarithms that mentions the mathematical concept of e.
1661 – Holland
Christiaan Huygens worked with the mathematical concept of e.
1683 – Switzerland
Jacob Bernoulli , in his studies of compound interest, derives the limit definition of the mathematical concept e
 , where
, where
- c is the annual compounding frequency of a 100% interest investment.
- the equation holds true for any real number c >=1.
Bernoulli wrote that e was between 2 and 3.
1690-91 – Germany, Holland
The mathematical concept e was first described by the letter b by Gottfried Leibniz in letters to Christiaan Huygens in 1690 and 1691.
1727 – 1748 – Switzerland
Leonhard Euler started to use the letter e in various publications and letters.
A lot of youtubers and authors, with no data to back it up as far as I know, claim that Euler did not use the letter e because of his last name; I call bullshit on that one.
This guy was arguably the most prolific and influential mathematician of all time. Let’s give him the e for Euler.
In 1748, Euler showed that e equals the sum of an infinite series:
e = 1/1 + 1/(1×2) + 1/(1x2x3) + 1/(1x2x3x4) + …. or
e =  where
where
- n are the integers 0,1,2… and
- n! = n “factorial” meaning: For c>0, c! = 1×2×3×4×…×c For n=0; 0! = 1
Euler approximated e to 18 decimal places = 2.718281828459045235
Ok, let’s dig a little deeper into the definitions of e that Bernoulli and Euler developed.
e Definition As A Limit
For the expression (1 + 1/c)c , as c approaches infinity, the expression approaches the value e.
e = Limc–>∞ (1 + 1/c)c
You can prove this to yourself by using a spreadsheeting tool or calculator.
You should be able to produce a table like the one shown below.
Table_Value of (1 + 1/c)n with increasing c

Jacob Bernoulli, in his studies of compounding interest, developed this in 1683.
Bernoulli’s Compounding Interest Analysis
Consider the Single Lump Sum Compounding Equation:
F = P(1+i/c)cy = P(1+r)n
Where
- F = Future Value
- P = Present Value
- y = number of years
- i = annual interest rate (typically the “stated rate”)
- c = compounding periods per year
- r = rate per period = i/c
- n = number of periods = (c)(y)
- Compounding Factor = (1+i/c)cy = (1+r)n
This can be useful in computing
- a future value of a lump sum for a specified interest rate and time period.
- the present value of a future lump sum payment, given a specific interest rate and time period.
- the time required for an investment to reach a certain future value, given a specific interest rate and initial investment amount.
It can also be used to derive the definition of Euler’s number e.
Bernoulli wanted to know what happens to the end-of-year value of an initial unit investment
- when invested at an annual rate of 100% with
- ever increasing compounding frequencies.
So, in terms of the lump sum compounding formula given above, he wanted to
- Compute F , given
- P = 1
- y = 1
- i = 100% and
- ever increasing values of c (the compounding period).
We can do these easily in a spreadsheeting tool or on our smart phone (Bernoulli couldn’t) and produce the table below.
Table_Lump Sum Compounding Formula Tables
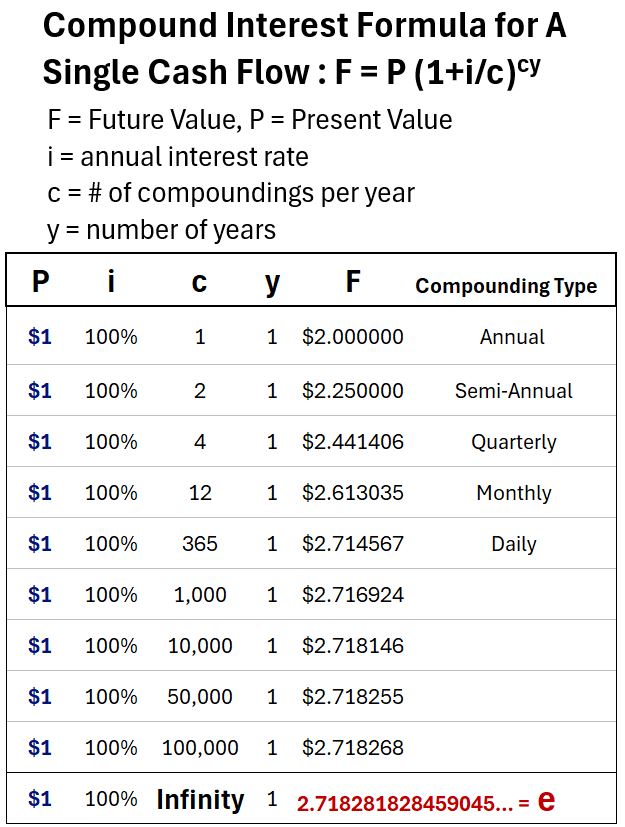
Graphically, if we plot the end of year value versus the number of compounding periods, the line asymptotically approaches e.
Picture_Graph of F at i = 100%, P=1, y =1, and c Increasing
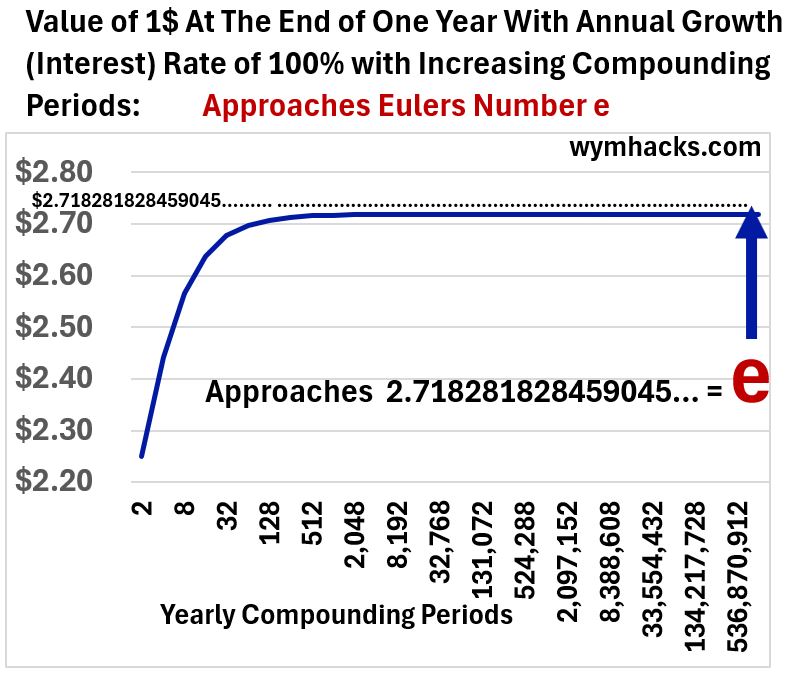
Bernoulli concluded that the value must be between 2 and 3.
You and I can use our powerful calculators (our smart phones!) and compute that as c gets bigger and bigger, F approaches the value e.
Lump Sum Compounding Formula Tables for Different Values of i and y
What happens if we change the rate and year inputs in our lump sum compounding formula?
Let’s look at a few examples in the tables below as we
- vary i (the rate) and
- y (the number of years) in our compounding formula
- and increase the compounding frequency c.
Table_Continuous Compounding with i = 7% and y = 10 years
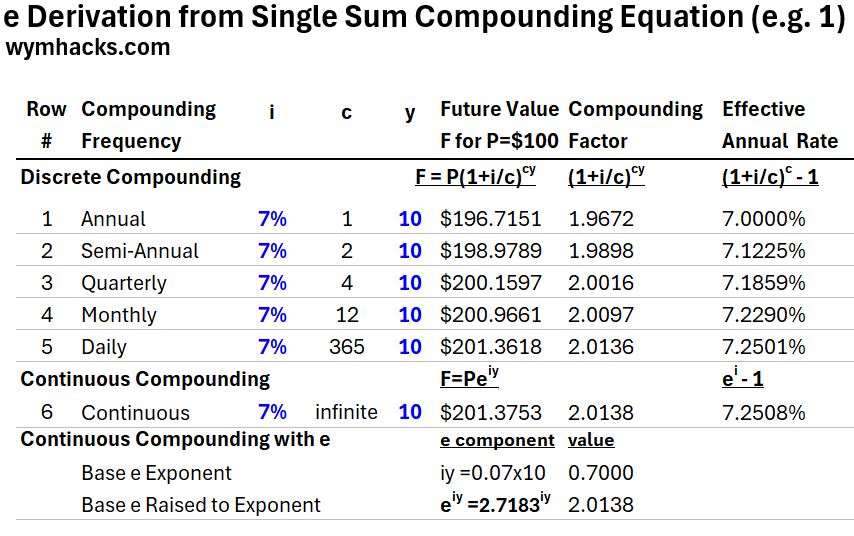
In Example 1 we show the classic rule of 70: i.e. 70/10 = 7% i.e. it will take roughly 70/i years to double the value of a single lump sum.
- The Continuous Compounding version of the Lump Sum Compounding Equation is F = P eiy.
- The continuous compounding factor is 2.0138 which is equal to eiy = 2.7183iy= 2.7183.7= 2.0138.
Table_Continuous Compounding with i = 50% and y = 1 years
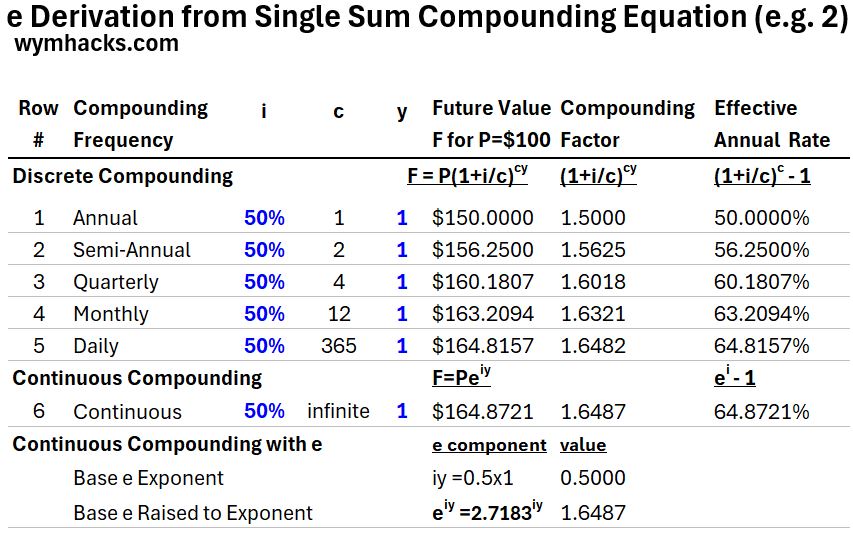
In Example 2 we let i = 50% and y = 1 year.
- The Continuous Compounding version of the Lump Sum Compounding Equation is F = P eiy.
- The continuous compounding factor is 1.6487 which is equal to eiy = 2.7183iy= 2.7183.5= 1.6487
Table_Continuous Compounding with i = 100% and y = 1 year
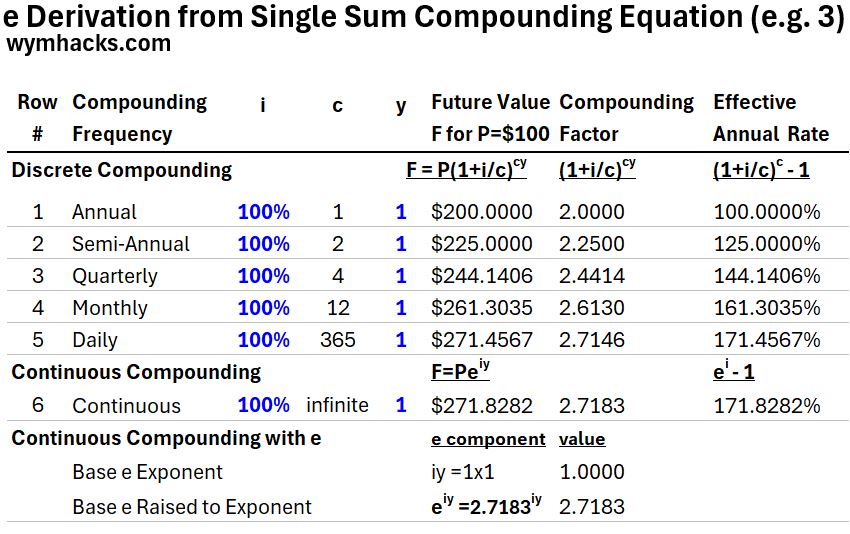
In Example 3 we let i = 100% and y = 1 year (which are the values we used to describe the Bernoulli derivation)
- The Continuous Compounding version of the Lump Sum Compounding Equation is F = P eiy.
- The continuous compounding factor is 2.7183 which is equal to eiy = 2.7183iy= 2.71831= 2.7183
So, from the above examples we see that for any value of i and y, the continuous compounding equation is always
F = P eiy = Equation for Continuous Compounding
Where the Future Value F can always be expressed as a function of base e raised to a “growth rate i x the number of years”.
- F = Future Value
- P = Present Value
- y = number of years
- i = annual interest rate (typically the “stated rate”)
In the next section we’ll do a little math to show how we can convert F = P(1+i/c)cy to its continuous compounding form F = P eiy.
Derivation of Continuous (Infinite) Compounding Equation
Refer to the great tutorials by Sal Khan on how to derive the infinite compounding formula.
Recall the Compound Interest Formula for a Single Cash Flow where,
- F = P(1+r)n = P(1+i/c)cy
- F = Future Value, P = Present Value,
- i = yearly interest rate (sometimes called the stated rate)
- c = number of compounding periods per year
- r = interest rate per compounding period = i/c
- y = number of years
- n = total number of compounding periods = (c)(y)
Start with our compounding formula.
(1) F = P(1+i/c)cy
Assume c is going to infinity. Then
(2) F = lim(c→∞) [ P(1+i/c)cy ]
Now we want to substitute and let x = c/i. So c = xi and i/c = 1/x.
Substitute for c and i/c in equation (2). We get,
(3) F = lim(x→∞) [ P(1+1/x)xiy ] which equals
(4) F = P [ lim(x→∞) (1+1/x)x ] iy . The limit expression in this equation we know is equal to e, Euler’s number, so,
(5) F = P e iy = Equation for Continuous Compounding
F = P e iy = Equation for Continuous Compounding
e Definition as an Infinite Series Summation
We mentioned in the history section that in 1748, Euler showed that e equals the sum of an infinite series:
e = 1/1 + 1/(1×2) + 1/(1x2x3) + 1/(1x2x3x4) + … or
e = 1/1! + 1/2! + 1/3! + 1/4! +…+ 1/n!+ …
e = 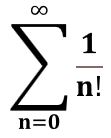 where
where
- n are the integers 0,1,2… and
- n! = n “factorial” meaning: For n>0, n! = 1×2×3×4×…×n For n=0; 0! = 1
- note: n factorial is the nth derivative of xn
- so for example, d4/dx(x4) = 1x2x3x4 = 4! = 4 factorial
He used this to approximate e to 18 decimal places:
e = 2.718281828459045235
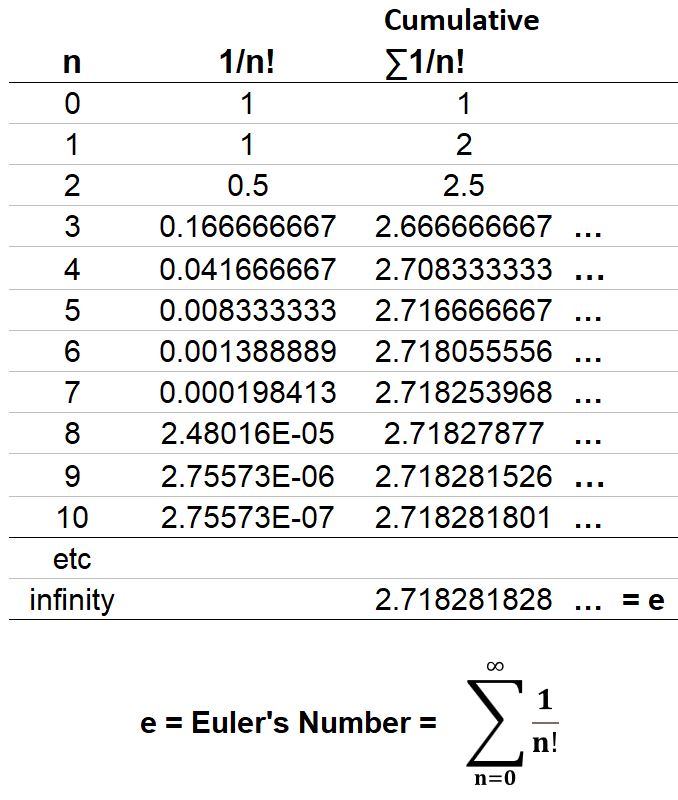
The table below shows the first 10 terms of the summation. You can see that by the 5th term we start getting close to the value e.
Table_Tabulation of 1/n! infinite series components of e
Unique Properties of e
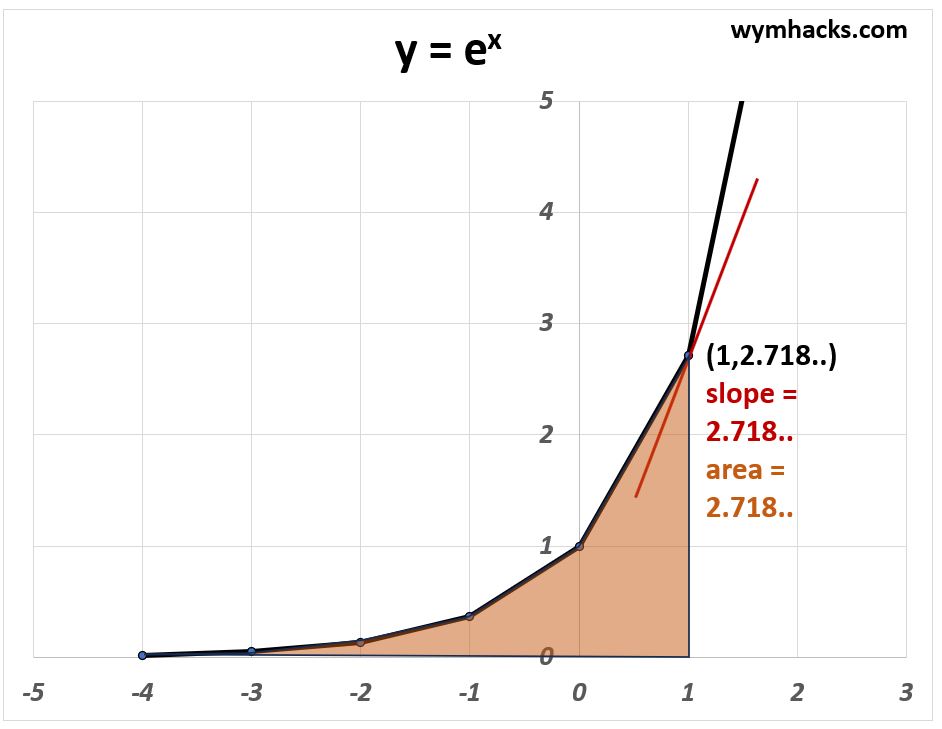
e can be expressed as a variable expression (a function): f(x) = y = ex .
The same limit and series formulas for e hold generically for ex. That is,
The exponential function (with Euler’s Number e) is the only function such that for every point on the graph y = ex,
- the y value for any value x is equal to the
- slope (derivative) at x which is equal to the
- area under the curve (left of point x)
So for example, at x = 1 (see the graph below):
- y = 2.718..
-
Derivative e with respect to x = f'(ex) = d/dx(ex) = ex = e1 = 2.718..
-
Area under curve (for x = <=1) = e1= 2.718..
Why is e important?
Note: I used Google Gemini to generate the below material.
- Natural Growth and Decay: Many natural phenomena, like population growth, radioactive decay, and compound interest, are modeled by exponential functions with base e.
- Calculus: The function e^x is its own derivative, making it incredibly simple to work with in calculus.
- Logarithms: The natural logarithm, ln(x), is the inverse of the exponential function with base e. It simplifies many mathematical calculations.
- Complex Numbers: Euler’s formula, e(iθ) = cos(θ) + i sin(θ), connects exponential functions with trigonometric functions.
- Probability and Statistics: The normal distribution, a fundamental concept in statistics, involves the constant e.
- Engineering and Physics: e appears in various engineering and physics equations, including those related to electrical circuits, heat transfer, and quantum mechanics.
- Economics: Exponential growth and decay models are used in economics to analyze economic trends and make predictions.
- Computer Science: e is used in algorithms and data structures, such as exponential search and binary search trees.
- Biology: e is used to model population growth, the spread of diseases, and other biological processes.
- Mathematics: e is a fundamental constant in many areas of mathematics, including number theory, analysis, and topology.”
Notes on the Natural Logarithm and Exponentials
Logarithms Came Before Euler’s Number e
- They were invented and used in the early 1600s to create shortcuts for finding solutions for complicated/tedious multiplications.
- This helped scientists in performing astronomical and navigation related calculations.
- Tables were created that helped simplify multiplications and divisions into easier additions and subtractions.
Example of Logarithmic Simplification
- A log is defined as: If logbx = n , then bn = x
- So Logarithms are exponents.
- First look up the base 10 logarithms of these number: log 100 = 2 and log 1000 = 3
- Add the logs: 2 + 3 = 5
- Find the answer in an antilog table: antilog of 5 = 100,000
Natural log Definition and Properties
- ln(x)=loge(x)
- x = eln(x)
- x = ln(ex)
- The natural logarithm (ln) and the exponential function (ex) are inverse functions
- ln(xy)=ln(x)+ln(y)
- ln(x/y)=ln(x)−ln(y)
- ln(xy)=yln(x)
- ln(e)=1
- ln(1)=0
- ln(1/x)=−ln(x)
Properties of Exponentials
- xaxb = xa+b
- xa/xb = xa-b
- (x/y)b = xb/yb
- (xa)b = xab
- (xy)a = xaya
- x1= x
- x0 = 1
- x-1 = 1/x
- x-a= 1/xa
- xm/n = nth root of xm = (nth root of x)m
Examples of Scientific Equations That Use The exponential Function
Note: this section was generated using Google Gemini
- Radioactive Decay Law
- Exponential Growth/Decay
- Charge on a Capacitor in an RC Circuit
- Current in an RL Circuit
- Continuous Compound Interest
- Population Growth Model
- Barometric Formula
- Planck’s Law
- Schrödinger Equation
Conclusion
- Euler’s Number e is a constant that equals 2.718281828459045…keeps going.
- It’s defined as
 , where
, where- c is the annual compounding frequency of a 100% interest investment.
- The equation holds true for any real number c >=1
- It’s also defined as
e =
 where
where- n are the integers 0,1,2… and
- n! = n “factorial” meaning: For c>0, c! = 1×2×3×4×…×c For n=0; 0! = 1
- e is a constant that is Real, Irrational, and Transcendental.
- e indicates exponential, continuous growth.
- Many natural phenomena exhibit this behaviour.
- The mathematical properties of y = ex make it a powerful tool in calculus.
Check out the reference material below for more:
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.