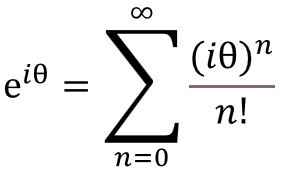Menu (linked Index)
Complex Numbers
Last Update: November 29, 2024
- Introduction
- Multiplying by -1
- The Imaginary Unit i
- Multiplying by i
- Complex Numbers and Complex Plane
- Multiplying by i in the Complex Plane
- Polar / Trigonometric Form of a Complex Number
- Polar / Exponential Form of a Complex Number
- Euler’s Formula is All about Rotation
- How Useful are Complex Numbers?
- Conclusion
Introduction
Every other number you deal with belongs to the subset of numbers called Complex Numbers.
They can be represented as z = a + bi where a is called the Real Part and b is called the Imaginary Part.
i is called the Imaginary Unit and = ![]() . It was invented in order to find Non Real Solutions to equations like y = x2 + 1.
. It was invented in order to find Non Real Solutions to equations like y = x2 + 1.
But its real power comes in its ability to model the wave like physical behaviour of a lot of our world (e.g. subatomic behaviour, light, oscillatory movements of all sorts, etc.).
So let’s talk about Complex Numbers.
You can learn more about Complex Numbers and related topics via my other posts listed below:
Multiplying by -1
Multiply -1 by itself successively and you get a repeating pattern 1,-1,1,-1,etc.:
- (-1)0 = 1
- (-1)1 = -1
- (-1)2 = 1
- (-1)3 = -1
- etc.
Think of a (Real) number on the (Real) number line X.
If you multiply X by successive (-1)s , it will toggle or flip back and forth (between two conditions or states) X and -X.
Picture_X Flipping on the Number Line
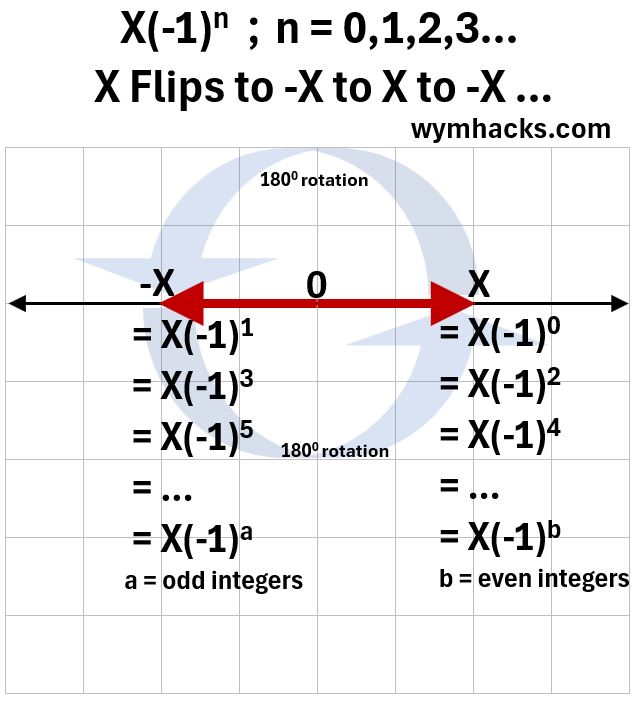
So, in addition to being scalable, Real Numbers, if signed, exhibit one dimensional rotation.
Imaginary Unit i
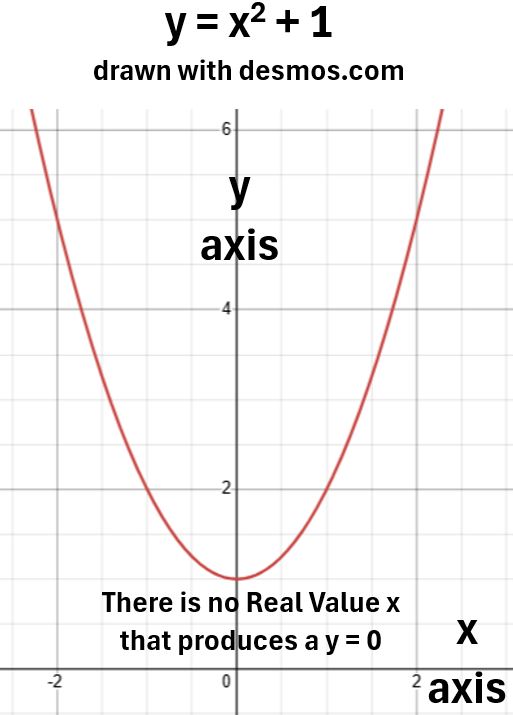
Consider the polynomial function y = x2 + 1.
What values of x will make y = 0 i.e. x2 + 1 = 0?
- x2 + 1 = 0
- x2 = -1
- x = square root (-1) =

You were taught in high school that when you saw a solution containing the square root of a negative number, that it could not be a Real Number.
There is no Real Number x that will cause y = 0 . The graph of y = x2 + 1 makes this obvious.
Picture_Graph of Function y = x2 + 1
So, how do forward thinking mathematicians get around this?
They invent a number that equals √(-1) and they eventually symbolize it with a lowercase “i”.
- i = the Imaginary Unit =
 = the square root of -1
= the square root of -1 - By definition this is not a Real Number. It is not found on the Real Number Line.
- The concept of i was born out of trying to solve cubic equations
- The idea of
 was inspired by math dueling italian mathematicians in the 1500s!
was inspired by math dueling italian mathematicians in the 1500s!  substituted into the negative square roots of polynomial solutions allowed further manipulation and simplification of solutions.
substituted into the negative square roots of polynomial solutions allowed further manipulation and simplification of solutions. - See this great video: How Imaginary Numbers Were Invented (Veritasium)
- The idea of
- Rene Descartes (1596–1650) described
 as “imaginary” in his work “La Géométrie” (circa 1637).
as “imaginary” in his work “La Géométrie” (circa 1637).- He thought the concept was somewhat absurd ,so his description was meant to be derogatory.
- This guy was a philosopher mathematician. The saying “I think, therefore I am” is his.
- Descartes also invented the Cartesian Coordinate System (which uses two perpendicular axes to locate points in a plane.)
- Leonhard Euler (1707-1783) introduced the notation “i” for the imaginary unit around 1777.
Multiplying by i
If we keep multiplying i against itself we get a repeating set of numbers (1, i, -1, -i, …repeating):
- i0 = 1 (any number raised to the zero is 1)
- i1 = i
- i2 = -1 (this is the definition of i)
- i3 = i2i1 = – i
- i4 = i3i1 = 1 (the beginning of a new cycle)
- i5 = i4i1 = i
- i6 = i5i1 = – 1
- i7 = i6i1 = – i
- i8 = i7i1 = 1 (the beginning of a new cycle)
- etc.
If we multiply (-i) by itself we’ll get (1, -i, -1, i…repeating):
- i0 = 1 (any number raised to the zero is 1)
- -i1 = – i
- (-i)2 = (-i)(-i) = i2 = -1
- (-i)3 = (-i)2 (-i1) = (-1)(-i) = i
- i4 = (-i3)(-i1) = (i)(-i) = 1 (the beginning of a new cycle)
- etc.
To summarize the above:
- If we multiply successive (i)s, the pattern is 1, i, -1, -i
- If we multiply successive (-i)s, the pattern is 1, -i, -1, i
Similar to what we did with (-1) , lets multiply a real number X by successive (i)s and plot the results on the Real Number Line.
Picture_X Flipping on the Number Line
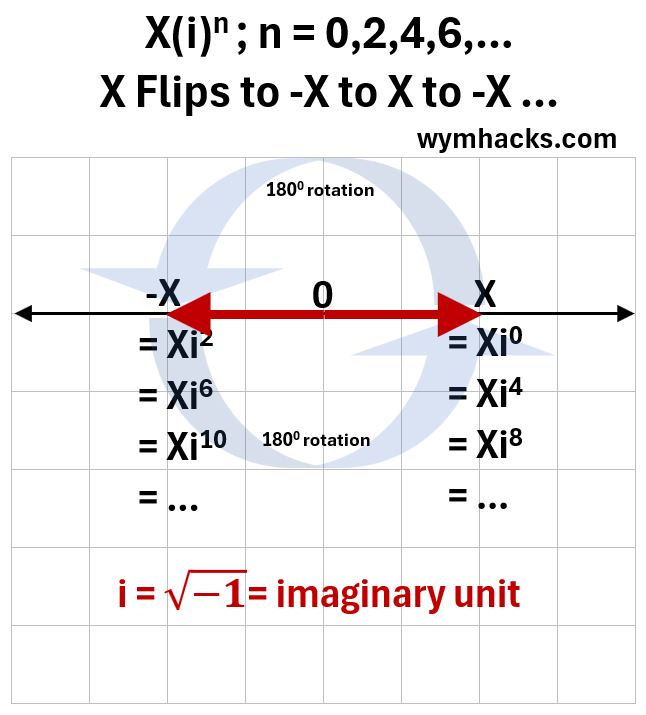
There are three observations you should make from the above graph
- Using the Real Number line, the only values we can plot will be when the multiples of i convert to 1 or -1
- You can not plot Xi or -Xi on the Real Number line
- Multiplying X times multiples of (i) , flips X to -X to X in a counter clockwise direction (as shown in the graph)
- If we had graphed X times multiples of (-i), the “direction of the flip” changes (the arrows now move clockwise)
How can we also plot the Xi and -Xi values so we can get a more complete picture?
Answer, expand Real Numbers so they have a second dimension.
Complex Numbers
Complex Numbers Defined
Picture_Number Classification Chart
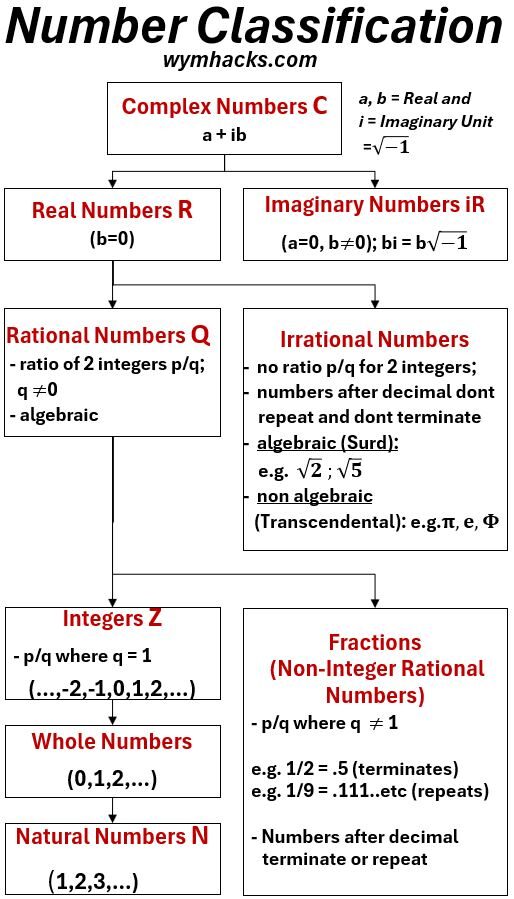
- (Rational/Irrational Numbers,
- Integers/Fractions,
- Whole Numbers and
- Natural Numbers)
- Example: 5 can be express as 5 +0i.
- were first used by Girolamo Cardano (1501-1576); see here and here.
- were coined by Karl Friedrich Gauss (1777-1855); see here.
- assume the form z = a + bi where
- z = the Complex Number.
- a = the Real Part of the Complex Number
- b = the Imaginary Part of the Complex Number
- think of b as the Real Number coefficient of the Imaginary Unit i
- think of bi as being the Imaginary Number
Graphical Representation of Complex Numbers
Complex numbers can be graphed on a special x, y coordinate system called the Complex Plane.
The Complex Plane is a 2 dimensional coordinate system that has Cartesian characteristics (it has an x axis and a perpendicular y axis).
- The x coordinates make up a Real Number line (horizontal, just like a regular Cartesian x axis).
- The y coordinate is the imaginary number line (just like the vertical y axis of a cartesian x,y graph.
According to [A Short History of Complex Numbers. Orlando Merino.University of Rhode Island.January, 2006], the Complex Plane, also known as the Argand diagram, was independently discovered by two mathematicians:
- Caspar Wessel (1745-1818): Published Complex Plane concept in 1799
- Jean-Robert Argand (1768-1822): Published in 1806.
While Wessel’s work was largely unnoticed at the time, Argand’s publication gained more attention and helped popularize the concept.
Ok, let’s see how some example Complex Numbers would look in the Complex Plane.
Plotted below are four example Complex Numbers which are plotted on the graph below.
- z1 = 2 + 2i
- z2 = -2 + i
- z3 = -3 – 2i
- z4 = 2 – i
Picture_Complex Numbers on the Complex Plane
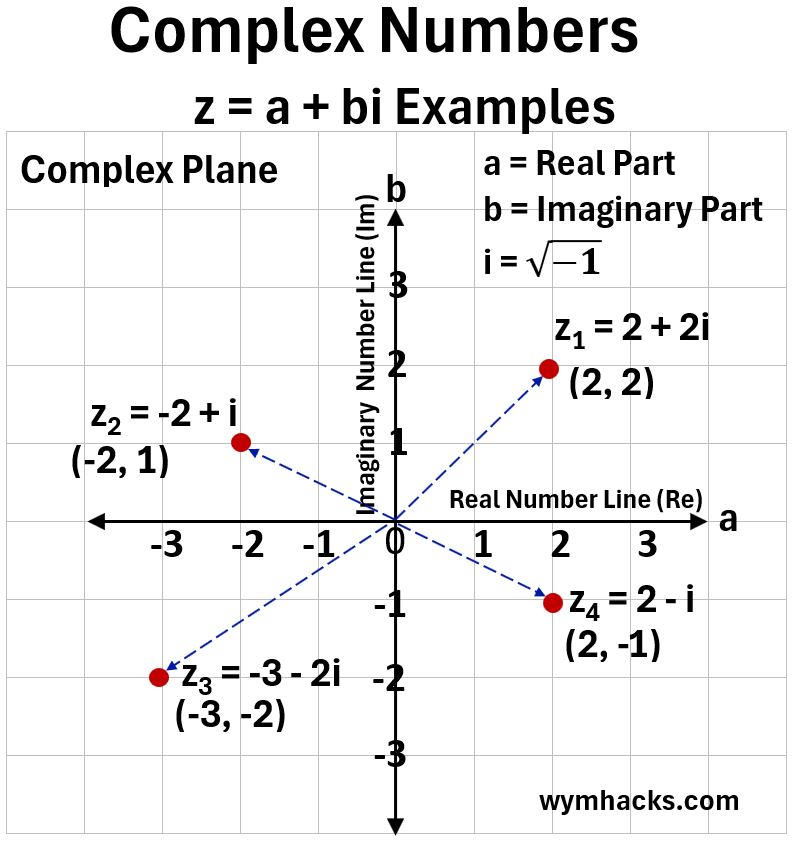
The complex numbers are plotted just like (x,y) in a cartesian coordinate system but we’ll call them (a,b).
- a is called the Real Part of the Complex Number and is read off the horizontal axis
- b is the Real coefficient of the bi term and is called the Imaginary Part (somewhat misleadingly).
- bi is called an Imaginary Number
- The dashed lines drawn from (0,0) to the Complex Numbers have magnitude and direction
- These will add like mathematical vectors but will not multiply like them.
- So we will call them Complex Vectors or c-vectors
Multiplying by i on the Complex Plane
Assume X is a real number sitting on the Real Number axis of a Complex Plane (see the graph below).
If we multiply X by i successively, the result will flip by 90 degree counter-clockwise movements to Xi, then to -X, then to – Xi and back to X, where the cycle repeats.
Picture_Multiplying by i on the Complex Plane
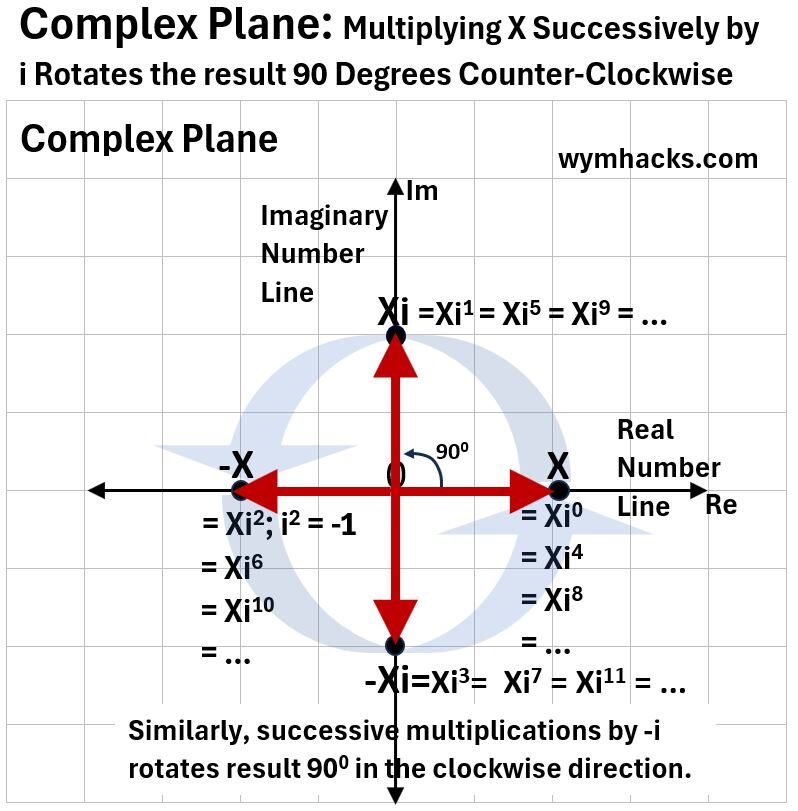
So, in this case, successive multiplications by i flips the result through 4 different states in the Complex Plane and then repeats.
In general , to rotate a Complex Number by 90/x degrees on the Complex Plane, multiply that number by i1/x (i.e. the xth root of i).
- For example, to rotate z by 30 degrees = 90/3, then multiply z by i1/3
- For example, to rotate z by 45 degrees = 90/2, then multiply z by i1/2
We see that i is a rotating (oscillating) machine in the Complex Plane.
Let’s take the Complex Number z = 2+2i and multiply it successively by i.
Picture_Rotating the Complex Number 2 + 2i
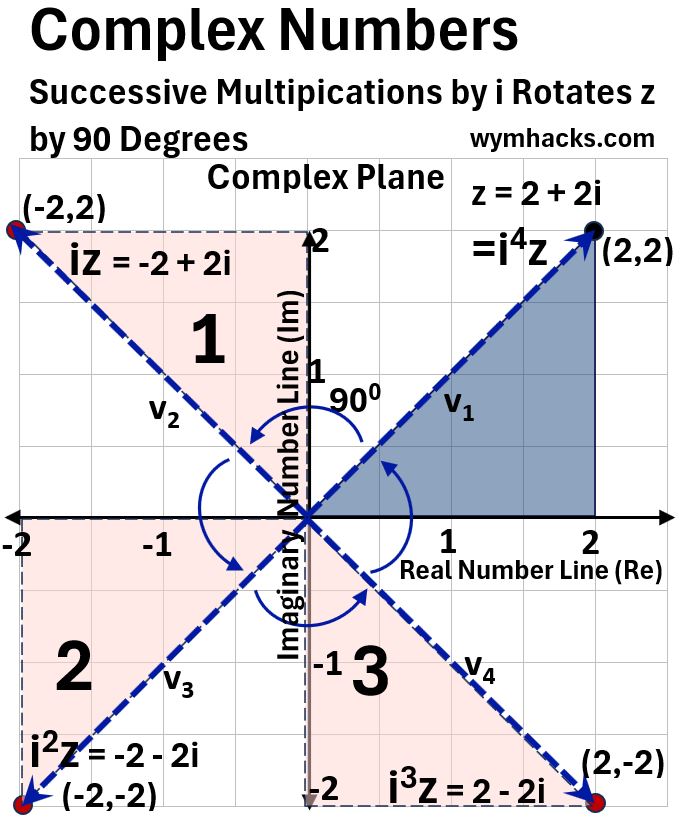
From the graph:
- z = 2 + 2i is represented as a point on a right triangle
- The complex vectors (c-vectors) are labeled v1, v2, v3, v4
- They have magnitude and direction and will add and subtract like mathematical vectors.
- Multiplying by successive (i)s moves the c-vectors and the triangles 90 degrees counterclockwise until
- we get back to the starting point z =i4z.
Looking at z as a c-vector or as part of a right triangle comes in very handy.
You see how multiplying by i has the effect of rotating the complex number (the triangle, or the c-vector) around the center of the Complex Plane.
Complex Numbers can therefore describe a combination of scaling and two dimensional rotation.
Polar / Trigonometric form of a Complex Number
Let’s place a generic Complex Number z = a + bi on the Complex plane as shown in the graph below.
Draw a right triangle with the hypotenuse being the Complex Vector (c-vector) for z = a + bi.
- The magnitude (length) of the c-vector is called the Modulus “r”.
- The angle θ between the c-vector and the positive Real Axis is called the Argument
- The vertical and horizontal legs have length “b” and “a” respectively.
Remember the Trigonometric mnemonic SOHCAHTOA to derive the following:
- sinθ = Opposite/Hypotenuse = b/r; b = rsinθ
- cosθ = Adjacent/Hypotenuse = a/r; a = rcosθ
- tanθ = b/a
- tan-1b/a = arctangent b/a = θ
We can now find a useful mathematical form for z = a + bi by substituting for a and b
- z = a + bi ; Rectangular Form of a Complex Number
- z = rcosθ + (rsinθ)i
- z = r(cosθ + isinθ) ; Polar / Trigonometric Form of a Complex Number
Note that “polar” comes from Greek meaning pole or axis. In geometry, Polar means expressed as
- a distance from the origin (axis or pole) and
- an angle from a reference point.
Picture_Trigonometric Properties of Complex Numbers
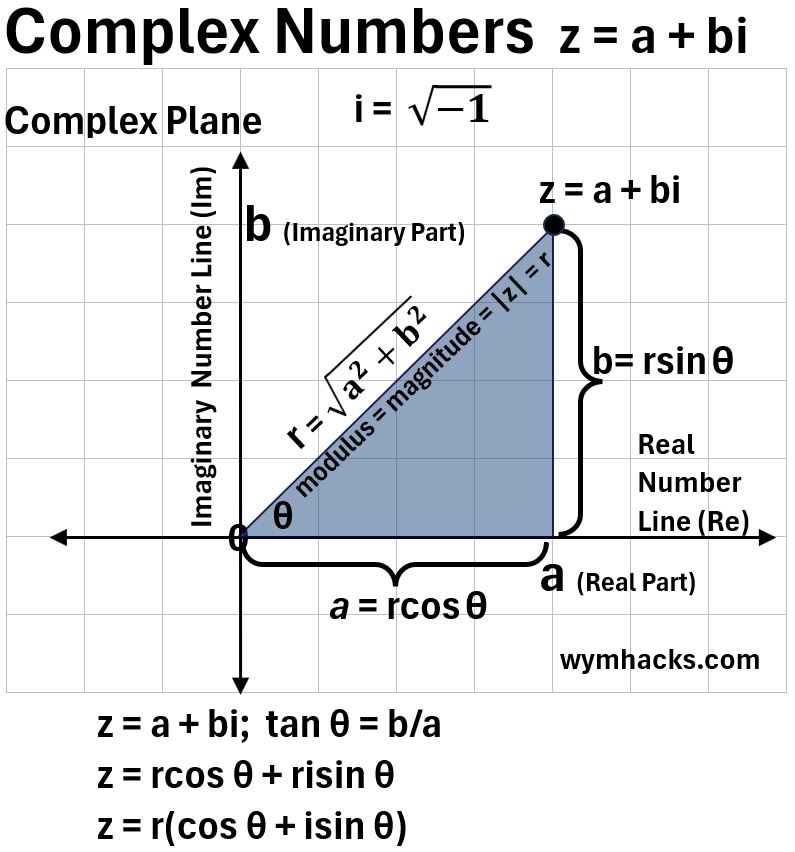
note: There is a possibly confusing issue with the complex number notation.
- Notice in the graph above that we have written the imaginary part as b even though it actually represents a multiple of i or bi.
- So technically, the height in the right triangle should really be bi
- This washes out in the end because we add i back when we express b as part of the complex number z.
So, we now have a Rectangular and a polar / trigonometric form of a Complex Number. Is there any other interesting way to express this?
Polar / Exponential Form of a Complex Number (Euler’s Formula)
I’m going to pull a Rabbit out of a hat here and just tell you that there is a mathematical formula called Euler’s Formula that states:
eix = cosx + i sinx ; for any real number x
We want to incorporate it into our understanding of Complex Numbers.
Since x is any real number, I am just going to replace x with θ , a more common angle symbol.
eiθ = cosθ + i sinθ
You really should link to my post: Euler’s Formula and see how this formula is derived.
Knowing the derivation will
- help you learn or remember a little calculus, algebra, and trig. ,
- make you “believe it” and
- give you a deeper appreciation of its elegance and simplicity.
Now, In the last section we derived a polar / trigonometric form for a Complex Number:
z = r(cosθ + isinθ) ; Polar / Trigonometric Form of a Complex Number
But , we now recognize that the expression in the parenthesis above is Euler’s Formula. So we can re-write z as:
z = reiθ ; Polar / Exponential Form of a Complex Number
Please note that the derivatives of sinx and cosx used in the derivation of Euler’s Formula require that the units of x be in Radians (and not Degrees).
Euler’s Formula is All About Rotation
Ok, so for any real number θ , where theta is going to be an angle,
z = r(cosθ + isinθ) = reiθ.
Let’s take the triangle we drew in the last section and put a circle of radius r around it.
We’ll get the picture below (remember we are using the Complex Plane).
Picture_Euler’s Formula: Part of a Circle in the Complex Plane
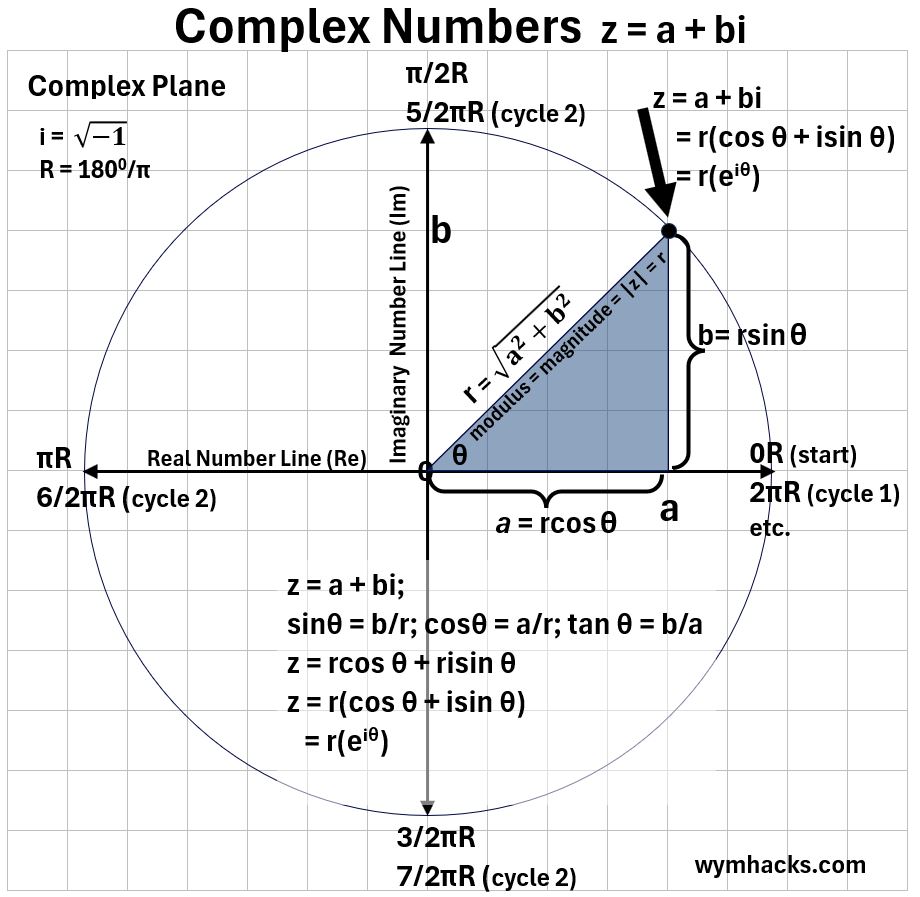
So, we see that a complex number which can be expressed as
- z = a + bi (Rectangular Form)
- z = r(cosθ + isinθ) ; Polar / Trigonometric Form of a Complex Number
- z = reiθ ; Polar / Exponential Form of a Complex Number
can be shown on the complex plane as a point on the circumference of a circle.
For different values of angle θ, z is going to move along the circumference.
z Rotates Around a Circle for Changing θ s
Let’s explore this circular movement by calculating some Euler’s Formula values and graphing them on the complex plane.
So, we want to graph eiθ for different angles θ.
Recall (or read my post on Euler’s Number e or my post on Euler’s Formula) that
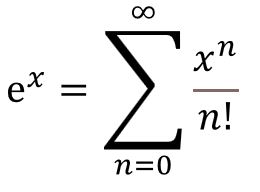
and we can substitute x for iθ to get
Now
- expand this equation to a sufficient amount (lets say n = 0 to 100) and
- for different values of θ,
- compute the value of eiθ.
- Plot the results on Complex Plane coordinates.
I’ve done this using my Excel spreadsheet tool. The results are tabulated below for three angles:
- 1/4π Radians,
- 1/2π Radians, and
- 1π Radians.
Each value is plotted starting at the center of the circle in the complex plane and then we can move it right, up, left, and down depending on the sign and whether the value is the real value or the imaginary value of the complex number.
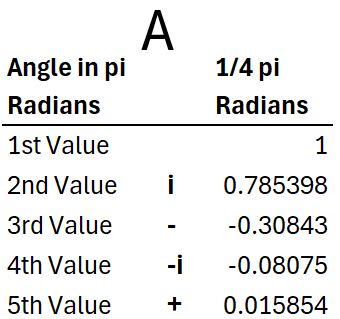
Real and Imaginary Series Values of eiθ for θ = 1/4 π Radians
For example, if you take a look at Table A (results for 1/4 π Radians) and then the graph below, you can trace out the path from the center of the circle which goes
- right 1 (real)
- up .785 (imaginary)
- left .308 (real)
- down .08 (imaginary)
- right .0158 etc….the terms getting smaller and smaller.
- We ultimately arrive at the point A which has a value
- z = a + bi = .707a + .707b
- The values .707 and .707 are the summation of the real terms and the imaginary terms respectively.
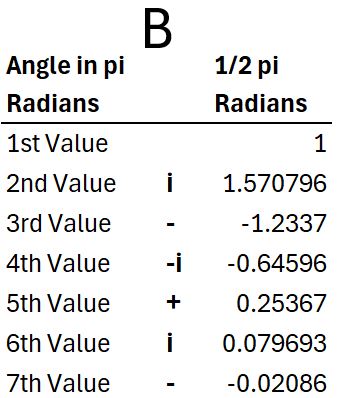
Real_and Imaginary Series Values of eiθ for θ = 1/2 π Radians
For θ = 1/2 π Radians, you can follow the path for B in the chart below as well. Here we start from the center of the circle and then move
- +1 (Real)
- +1.57 (Imaginary)
- -1.23 (Real)
- -.64 (Imaginary)
- +25 (Real)
- continuing to spiral to the point (0,1)
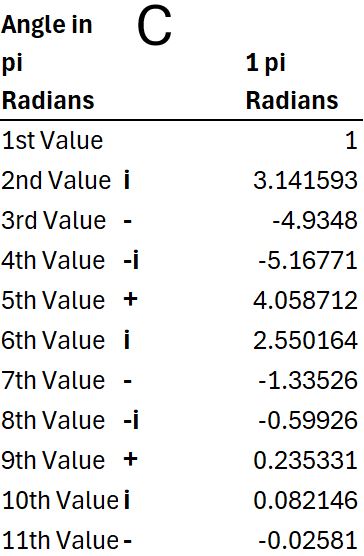
Real and Imaginary Series Values of eiθ for θ = π Radians
For θ = π Radians, you can follow the path for C in the chart below.
Summing up all the infinite series terms will get us to the point (-1,0).
Graph_z Walks A Circle In The Complex Plane
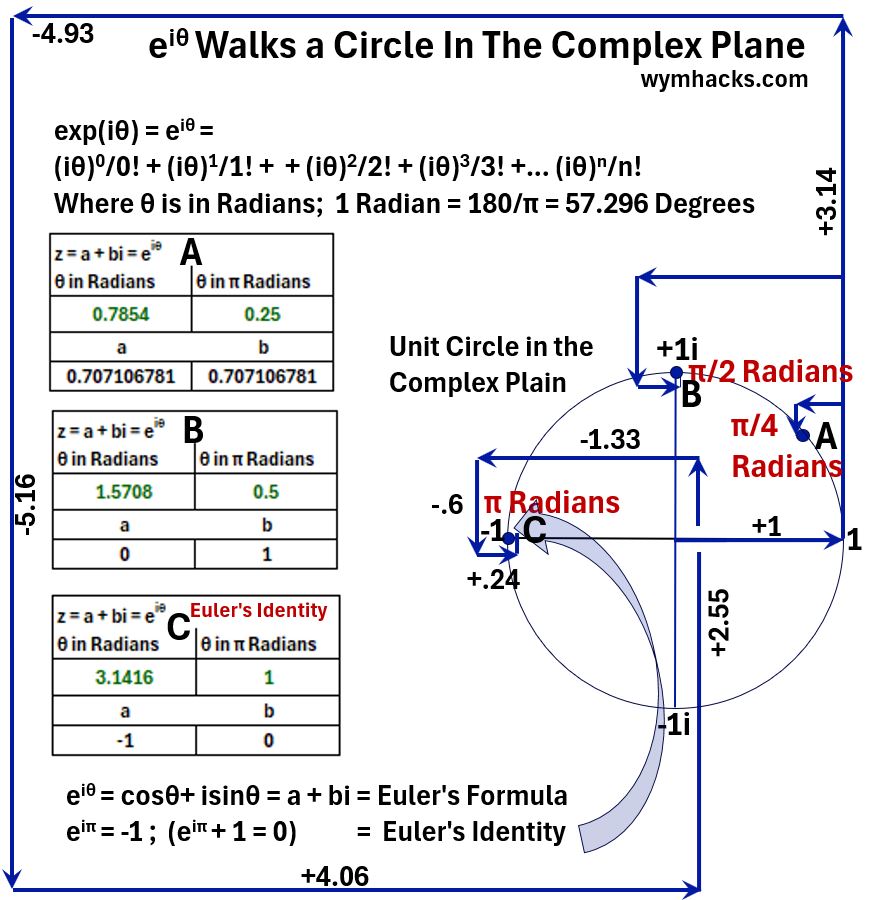
Notice what happens when we assume the angle is π Radians (Case C).
The result z = eiθ = -1 (it sits on the real number line at -1).
We’ve seen this expression before.
Its Euler’s Identity when we substituted π in for θ in Euler’s Formula
eiπ + 1 = 0 ; Euler’s Identity
This is a wild graph (see this amazing video and explanation by Grant Sanderson at 3Blue1Brown).
Notice how differently sized vectors (components of the complex numbers) spiral out with consecutive 90 degree turns but always converge back to a point on the circumference of a unit circle in the complex plane.
Any angle we choose will produce these 90 degree turning spirals which will ultimately land on the unit circle.
Euler’s Formula:
If we plug in iθ, for different θ the value eiθ will move around the circumference of a circle in the complex plane.
Euler’s Identity:
If we plug in π for θ, eiπ + 1 = 0
How Useful are Complex Numbers?
While initially conceived to help solve or simplify cubic polynomials, today complex numbers are utilized in numerous scientific and engineering applications.
Historical Progression of the Concept of i and Complex Numbers
We learned about how Complex Numbers first started appearing in the 1500s as Italian mathematicians tried solving cubic equations.
- Equations that didn’t have Real solutions could be further simplified by using the imaginary number i (where i2 = -1.)
In the 1700’s, mathematicians visualized complex numbers as points on a plane called the complex plane, giving them a geometric interpretation.
In the 1800’s, the Fundamental Theorem of Algebra was developed. It states (and assumes) the following:
- If we have an nth degree polynomial f(x) =axn+bxn-1+…k (where k is a constant), then
- it will have exactly n roots i.e. n values for x that will make f(x) = 0.
- The coefficients can be complex numbers.
- The roots can be complex numbers and there must at least be one if any of the coefficients are complex numbers.
- This theorem says that complex numbers are essential for understanding the complete solution space of polynomial equations.
Complex Numbers are Not Just Used in Pure Mathematics
By extending the number system to the Complex Plane, we elevate numbers from one-dimensional entities to two-dimensional quantities.
The geometric aspect of Complex Numbers allows them to be applied in many scientific fields.
We’ve seen that Complex Numbers have a periodic rotational aspect which allows them to used in the modelling of many natural phenomenon.
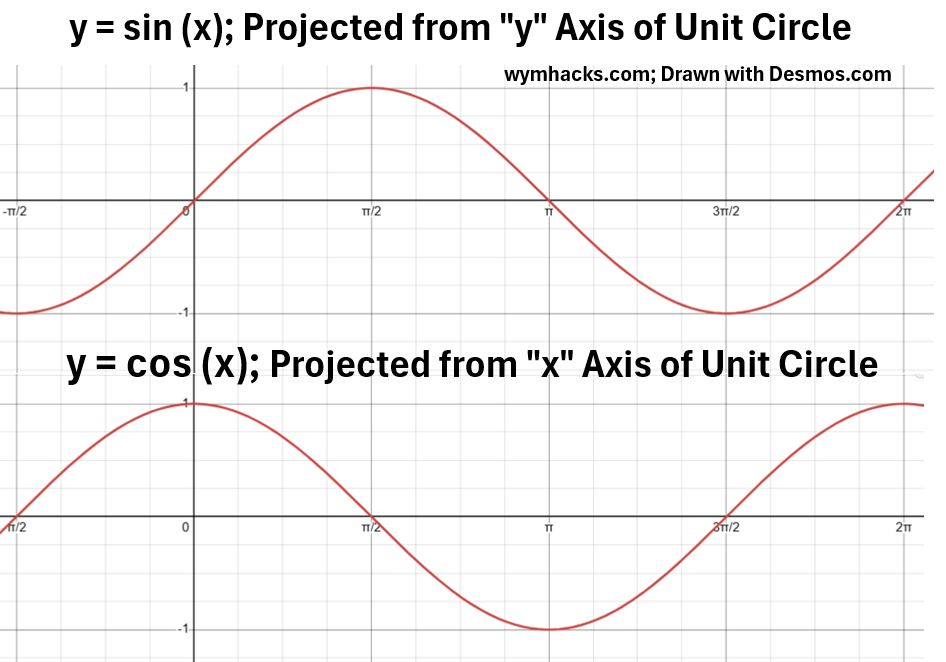
For example, if we take the motion of eiθ in the complex plane, we can project sinusoidal patterns onto magnitude vs angle graphs as shown below.
This can be used to model wave behaviour which is exhibited by many natural phenomena like
- Water Waves,
- Sound Waves,
- Light Waves,
- Seismic Waves,
- Matter Waver (subatomic particles like electrons).
Examples of fields where Complex Numbers are heavily applied:
The list below was generated using Google Gemini.
- “Electrical Engineering
- AC Circuit Analysis
- Signal Processing
Quantum Mechanics:
- Wave Functions
- Quantum Computations
Control Systems:
- System Analysis and Design
Fluid Dynamics:
- Fluid Flow Analysis.”
Complex numbers can simplify solving mathematical descriptions of real world problems.
- Euler’s formula z = eiθ = cosθ + i sinθ allows for the transformation of trigonometric expressions into simpler exponential forms.
- In exponential format, multiplication and division are simplified to addition and subtraction
- example 1: z1z2 = r1eiθ1r2eiθ2 = r1 r2 ei(θ1+θ2)
- example 2: z1/z2 = r1/r2 ei(θ1-θ2)
Conclusion
We’ve described how Complex Numbers unify the Number Classification System. That is , all numbers can be expressed as Complex Numbers.
- Complex Numbers describe a combination of scaling and two dimensional rotation.
- Real Numbers can scale and ,if signed, exhibit one dimensional rotation.
- Multiplying a Real Number by -1 transforms it, by flipping it 180 degrees on the Real Number Line.
- Multiplying a Real Number by an imaginary number i transforms it by flipping it 90 degrees.
- Flipping 90 degrees makes no sense unless we have a two dimensional system where we can do this.
- The Complex Plane is this two dimensional system
- Complex Numbers (actually all Numbers) can be expressed as z = a + bi on the Complex Plane, where a and b are real and imaginary parts, respectively.
- They can be expressed in rectangular or polar form
- z = a + bi (Rectangular Form)
- z = r(cosθ + isinθ) ; Polar / Trigonometric Form of a Complex Number
- z = reiθ ; Polar / Exponential Form of a Complex Number
Complex Numbers are all about rotation in the Complex Plane.
Due to their periodic, oscillatory, sinusoidal nature, Complex Numbers model many natural phenomena and so are used to increase our
- understanding of the world (e.g. quantum mechanics and our understanding of the subatomic world)
- and our control over it (e.g. control and use of electricity, design of new products and technology, etc.)
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.