Menu (linked Index)
Electricity (4/11) – Fundamental Physics
Last Update: January 15, 2026
Introduction
This is the fourth installment in a series of posts on electricity.
This section explores the fundamental laws governing energy conservation and transformation, defining Work as the mechanical transfer of energy through force and distance.
It establishes the relationship between thermodynamics and Power, providing the essential framework for understanding how energy is harnessed and used at a specific rate.
Navigation Index to Electrical Series Posts
Navigate to other posts in this series from the linked index below.
Electricity_(1/11 ) Introduction
Electricity_(2/11 ) Mathematical Foundations
Electricity_(3/11) Motion and Force
Electricity_(4/11) Energy, Work, and Power
Electricity_(5/11) Electrostatics, Current and Voltage
Electricity_(6/11) Electric Field, Magnetic Field, Current, And Voltage Relationships
Electricity_(7/11) Circuits, Resistors, Inductors, and Capacitors
Electricity_(9/11) AC Theory
Electricity_(10/11) Power Systems and the Grid
Electricity_(11/11) Timeline of Key Developments in Electromagnetism
On Line References
Listen, I could have easily listed 100 good references here.
There are indeed many on line references linked in many of my posts.
Here are a few I figured you should definitely have at your fingertips.
The first two are just good references for you to keep your units of measure straight.
The khanacademy.org link houses probably the greatest collection of STEM related videos, taught by several amazing teachers.
Finally, my “best of teachers” listing , gives you a certainly incomplete list of some amazing teachers that post their videos for free on the web.
- Symbols, Units, Nomenclature and Fundamental Constants in Physics – IUPAP 2010 – by Cohen and Giacomo
- NIST Office of Weights and Measures: www.NIST.gov SI units
- https://www.khanacademy.org/
- The Best On-Line Teachers
Law of Conservation of Energy
This fundamental principle states that energy cannot be created or destroyed; only transformed from one form to another (e.g., potential to kinetic, chemical to electrical, etc.).
The total amount of energy in an isolated system remains constant.
Technically, we can incorporate Einstein’s E = mc2 to make the definition a little more complete:
- The Law of Conservation of Mass-Energy states that the total amount of mass-energy in an isolated system remains constant.
- Mass and energy can be converted into each other, but their combined total is always conserved.
- Drop a ball from a height h.
- Assume no friction from the air etc.
- At any given moment in its path downward, its total energy is equal to the sum of
- its kinetic energy of movement and
- its potential energy of position
- Its total energy E is always constant and therefore conserved
- The values of the kinetic or potential energy may change
- e.g. KE is zero before the ball is dropped and PE is zero just before the ball hits the ground but
- The total energy E = KE + PE remains constant
- If we assumed friction, then the law still holds but
- we would have to account for the heat loss due to friction.
Laws of Thermodynamics
Thermodynamics is a branch of physics that deals with energy, heat, work, and temperature, and their relation to the properties of matter.
There are four thermodynamic laws which define how energy behaves in systems.
Zeroth Law (as in 0″th” law)
This one doesn’t excite me too much but for completeness , I’m including it.
If two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.
Basically, it defines temperature and allows us to use thermometers.
First Law of Thermodynamics
Check out these Khanacademy videos:
This is a statement of the Law of Conservation of Energy.
Energy cannot be created or destroyed; it can only be converted from one form to another.
That is, the total energy of an isolated system remains constant.
First law /Non Flow Equation
This law formalizes the conservation of energy in the context of heat, work, and internal energy within a system.
For a closed system (no mass coming in our out of whatever boundary we define) with no external kinetic or potential energy:
ΔU = Q – W = 1st law non-flow process
- U = internal energy = energy of the molecules in the system
- ΔU = change in internal energy of the system
- Q = heat added to the system
- W = work done by the system
- Work occurs on an object when it is moved a distance by a force.
For more details on the First Law check out my post: First Law of Thermodynamics
Second Law of Thermodynamics
Check out these Khanacademy videos:
No process is possible for which the total entropy (the number of possible “states”) decreases.
Conversely, the change in entropy of the universe will in reality always be greater than zero.
In theoretical conditions (reversibility), the change of entropy will be zero.
States are sometimes described as the extent of disorder (misleading) or randomness, but be careful:
- e.g. A room identical in every way including being at the same T and P , will not increase in entropy if I make the room messier.
- e.g. But if I increase the volume of the room, then its entropy will increase (regardless of whether the objects in the room are messy or not.
Entropy can be defined thermodynamically or statistically:
ΔS = Q/T (thermodynamic definition assuming constant temperature)
S = klnω (statistical definition)
where
- S = entropy
- ΔS = change in entropy of a system
- Q = heat added to the system
- T = temperature at which heat is added (in Kelvin)
- k = Boltzmann’s constant
- k relates the average kinetic energy of particles in a gas to the gas’s temperature.
- k = 1.380649… × 10⁻²³ J/K.
- ω = number of states a system can take on
Second Law Intuition Example
Check out this Khanacademy video on “Entropy intuition”
Imagine you have two reservoirs that are in contact with each other where hot reservoir 1 is at temperature T1 and cold reservoir 2 is at T2.
The temperatures will equalize as the heat transfers from the hotter reservoir 1 to the colder reservoir 2 (you’ll never see the opposite).
So, using the thermodynamic definition:
ΔS of the system = ΔS1 + ΔS2 = -Q/T1 + Q/T2 = Q/T2 – Q/T1
where the -Q and +Q indicate the heat flowing out (negative) of reservoir 1 and into (positive) reservoir 2.
Since T1 is bigger that T2, then Q/T1 is smaller than Q/T2
Therefore, ΔS will always be > 0 (2nd law of thermodynamics).
Third Law of Thermodynamics
I might as well mention this law as well.
The Third Law of Thermodynamics states that the entropy of a perfect crystal
- at absolute zero (0 Kelvin)
- is exactly zero,
- providing an absolute reference point for entropy measurement.
This is important because it allows scientists to determine the absolute entropy of substances, which is useful in computing thermodynamic properties.
Energy (Work or Potential Work)
Recall the first law of thermodynamics for non flow processes:
ΔU = Q – W (First Law for Non-Flow Process)
So we can say that Energy is the capacity to take in or produce heat or work.
For most practical purposes, this is a perfectly fine definition.
- Energy is a scalar quantity.
- Energy can be categorized as energy of motion or energy of position
- Energy of Motion = Kinetic Energy
- Energy of Position and/or Storage = Potential Energy
- SI units for energy: joule (J)
- 1 joule (J) = 1 newton-meter = 1Nm
- 1 newton (N) = 1 J/m
- While the joule (J) is the standard SI unit for energy (and work), other units are
- kilowatt-hour (kWh) for electrical energy,
- 1 kWh = 3.6e6 J = 3.6 million J (see section on power for watt definition)
- calories (cal) for thermal energy,
- The temperature of 1 gram of water will increase by 1 degree Celsius when one calorie of heat is put into it. (This refers to the “small” calorie, often denoted as “cal”).
- 1 thermal calorie = 1 cal = 4.184 J
- Be aware of the dietary Calorie (Cal). It is equal to 1000 thermal calories.
- The BTU (British thermal unit) is a common unit of measure for heating and cooling in England and the US.
- The temperature of 1 pound of water will increase by 1 degree Fahrenheit when one BTU of heat is put into it.
- 1 BTU = 1 British Thermal Unit = 1055.06 J
Work = Energy = (Force)(Distance)
If we apply a force on an object and displace that object in the direction of force, then we have done work on the object.
- Work is a measure of energy transfer.
- Work is energy transferred by a force.
- Work is a scalar quantity.
- W = work (don’t confuse with the unit of measure W = watt)
Work = (F)(cosӨ)(d) = FcosӨd
- F = force
- Ө = angle between force and displacement line
- F*cosӨ = the force component parallel to the displacement.
- d = displacement or distance
- W = Fd (when Ө = 0)
Picture: Example for Block of Mass m: W = Fd because Ө = 0
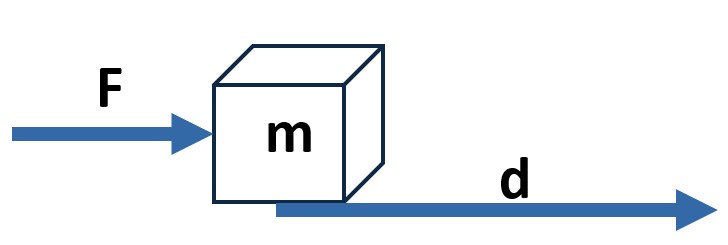
SI Unit for work: 1 joule = 1 J = 1 newton-meter = 1 Nm
Heat and work are
- forms of energy and
- both have units of joules.
Check out my dedicated post on this topic for more details (derivations, etc.): Work and Energy
References
The links below get you to some great Khanacademy videos. Watch them.
Power (Work Rate)
Here is a nice video on the topic:
Work and power – Mahesh Shenoy – Khanacademy
Power = Energy Rate = Work Rate
Power is defined as the
- rate at which work is done or, equivalently,
- the rate at which energy is transferred.
This means that a more powerful machine can perform the same amount of work in a shorter time.
The formula for power is:
Power = Work/time = W/t = ΔE/t
where:
- P = Power, measured in watts (W)
- W = watt (a unit of power)
- One watt is equal to one joule per second (1 W=1 J/s).
- t is the time interval, measured in seconds (s).
- ΔE is the change in energy, measured in joules (J).
- SI unit (base units): m2kg/s3
- SI unit (other units): J/s
- 1 W = 1 watt = 1 J/s = 1 m2kg/s3
In electrical power we will often see the Watt expressed as
- kilo Watts = kW = thousands of Watts
- mega Watts = MW = millions of Watts
- giga Watts = GW = billions of Watts
Whereas the kW is an energy rate, we can compute an energy quantity with the kilo Watt hour.
- 1 kilo Watt hour
- = 1 kWh
- = 1000 J/s* 60 s/min * 60 min/hr*1hr
- = 3.6 million J
- = 3.6e6 J = 3.6E6 J
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
