Exploring Euler’s Formula
Exploring Euler’s Formula
Last Update: December 18, 2024
Euler’s Identity
It all started for me when I came across the formula below. It’s called Euler’s Identity.
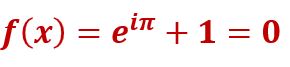
If you are a mathematician, you are getting pretty excited right now just seeing this equation.
- Kind of like a sportscaster’s reaction when you talk about “Mahomes” or
- a Swiftie’s response when you mention Taylor Swift.
All kidding aside, it’s a pretty simple (elegant?) expression that contains a lot of interesting mathematical terms.
So, I thought it would be fun to derive it and in the process maybe learn or remember a little math.
Euler’s Formula
In order to derive Euler’s Identity, you have to derive its progenitor first.
Euler’s Formula, shown below, relates Euler’s Number e, raised to the “ix”, to trigonometric functions cosine and sine.
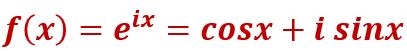
This is a bit bewildering to look at if you don’t have some basic understanding of i (the Imaginary Number) and a few other math concepts (like what a derivative is).
In the spirit of trying to explain every mathematical step, I ended up writing 6 articles.
Organization and Links
The articles are listed and linked below.
I wrote Articles 1, 2, 4, 5, and 6 below to provide some depth and context to Article 3.
You should read Article 3 first (derivation) and then Article 5 (incorporation into Complex Number format).
You’ll actually (probably) need to jump around to the various posts as needed, but you can do that via links in each of these articles.
I wrote these hoping that anyone with a high school level education should be able to understand.
- Unit Circle – Understand π, Radians, and basic trigonometric functions
- Number Classifications – Understand the basic Hierarchical order of numbers
- Euler’s Formula Derivation – Derive Euler’s Formula using Calculus, Taylor Series, Algebra, and Trigonometry
- Euler’s Number – Understand e
- Complex Numbers – Learn about the Imaginary Unit, Complex Numbers, the Complex Plan, and how Euler’s Formula Fits in
- Complex Number Math – Learn some basic Complex Number mathematical operations
Happy reading!
References
I think the references below are fantastic. If you search their web sites or you tube sites for “complex number” or “imaginary unit” or “Euler” you’ll find a lot of great videos taught by very smart and skilled teachers.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
