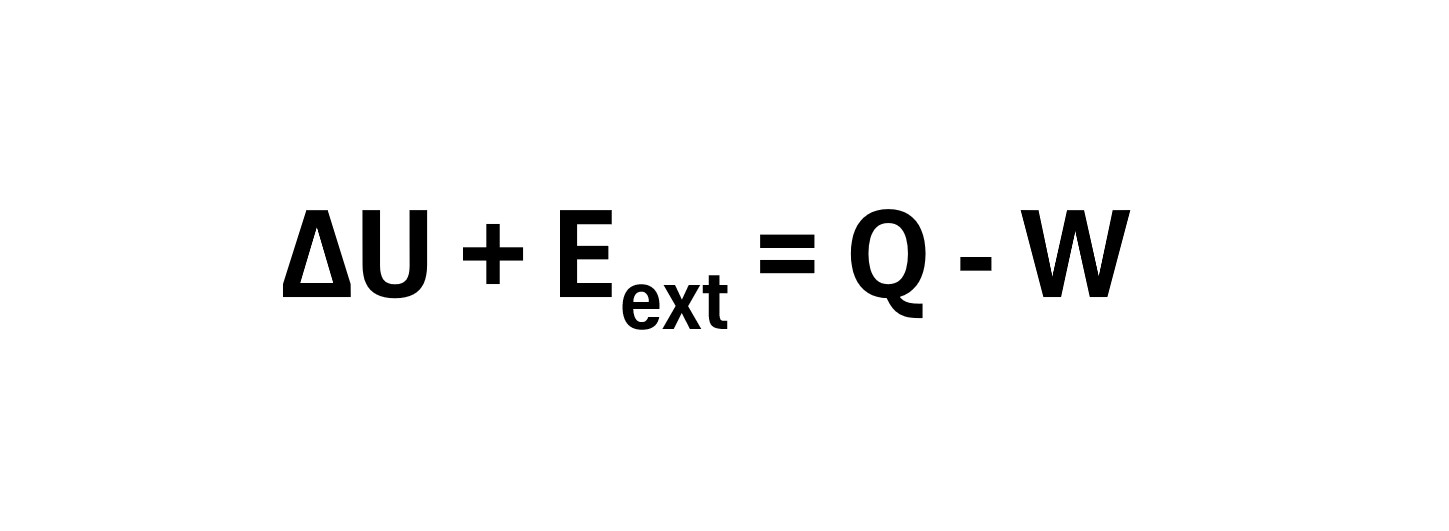First Law of Thermo – Dynamics

Leave a Comment / Physics, Science, Thermodynamics / By

Menu (linked Index)

First Law of Thermodynamics

Last Update: July 10, 2025 

Introduction

In this post, I describe some of the key aspects of the formula for the 1st Law of Thermodynamics (for closed systems i.e. no mass flow).

My goal is to give you a high level almost superficial understanding but hopefully enough to make you want to learn more.  

References/Sources

You have so much information at your fingertips for deeper learning. 

I’ve used all the following resources and found them helpful: 

Another way to get a deeper understanding is to learn more about the historical development of thermodynamic concepts and the key contributors. 

Consider learning more about:

  • Antoine Lavoisier (1743-1794) & Pierre-Simon Laplace (1749-1827) – Concepts of heat using calorimetry.
  • Sadi Carnot (1796-1832) – Heat engines and efficiency (work and heat relationships).
  • Julius Robert von Mayer (1814-1878) – Conservation of energy
  • James Prescott Joule (1818-1889) – 1840s experiments showing mechanical equivalent of heat
  • Hermann von Helmholtz (1821-1894) – Conservation of energy. Articulated that Energy changes form but is neither created or destroyed.
  • Rudolf Clausius (1822-1888) – 1850 Formally articulated the 1st Law of Thermodynamics. 

Return to Menu

Work and Energy

Work is force acting through a distance. 

Kinetic Energy

(1) dW = Fdl

Where F is is the component of the force acting in the direction of the displacement dl.

  • The dW and dl mean infinitesimal changes to the work W and displacement l.
  • The differentials account for those situations where the Force might not be constant 
  • By making the displacement super tiny (dl), we can assume the force remains constant and produces a tiny W or dw.
  • If the force is constant across the full displacement then the equation can be written as W = Fl  (or W = Fd more commonly).

You have to integrate equation (1) to determine the work for a finite process (from l1 to l2 for example).

From Newton’s 2nd Law of Motion:

(2) F = ma = mass*acceleration

More generally, 

(2.1) More generally,  F = ma/gc
  • gc is a proportionality constant.
  • gc = 1 (kgm)/(Ns2) when SI units are used and
  • gc = 32.174 (lbm ft)/(lbfs2) when English Engineering System (EES) units are used.
  • Many American engineering firms still use the EES.
  • If you don’t see the gc in the force formula, you can assume we are using SI units. 

Substitute (2) into (1): 

(3) dW = madl

Acceleration a is change of velocity v over change in time t: 

(4) a = dv/dt

Substitute (4) into (3):

dW = (m)(dv/dt)dl

rearrange:

(5) dW = (m)(dl/dt)dv

Velocity is the change of distance l over time t:

(6) v = dl/dt

Substitute (6) into (5):

(7) dW = mvdv 

Integrate for a finite change in velocity v1 to v2: 

(9) W = 1/2m(v2-v1) = 1/2mΔv= Kinetic Energy =ΔKE

This term was coined the Kinetic Energy by Lord Kelvin (William Thomson) in the period 1849-51. 

Potential Energy (of Gravitation)

We have to start with Newton’s Law of Universal Gravitation:

(10) Fg = G(m1)(m2)/r2
  • Fg = gravitational force
  • G= universal gravitational constant = 6.67e-11 Nm/kg2
  • m1, m2 = mass of objects 1 and 2
  • r = distance between objects (don’t confuse with radius)

Let’s reconfigure the equation to apply to an object on earth.

  • Fg = G(m1)(m2)/r2
  • Let m1 = mass of earth and m2 = m = mass of object on earth where
  • m1 = mass of earth =  ~5.97e24 kg
  • r = distance from center of object on surface (or “near” surface…see Note below) of earth to center of the earth = ~6378 km
  • so, Gm1/r2 = [(6.67e-11 Nm/kg2)(5.97e24 kg)]/(6378 km)2  =
  • g = ~ 9.8 m/s2 . So, 
(11) Fg =  mg = Gravitational Force between earth and object with mass m.

Note, for objects further away from the earth (e.g. satellites), Gm1/r2  wont be “g” anymore as r becomes significantly larger than the earths radius

If we want to lift an object a distance from h1 to h2, then the work done will be

(12) W = Fg* distance

Substituting for Fg and h we get, 

(13) W = mg(h2-h1) = mgΔh = Gravitational Potential Energy = ΔPEg

This term was coined Potential Energy in 1853 by William Rankine.

Kinetic and Potential Energy can be Macroscopic or Microscopic

I want to make sure we are clear on this before we delve into more detail below. 

The kinetic energy of motion and the potential energy (of position) are

  • always present on a microscopic scale and
  • can be present on a macroscopic scale.

That is, a substance can be moving in space or be positioned in space such that it has kinetic or potential energy.

  • This describes the object as a whole (i.e. macroscopic)

But every object or substance is made up (internally) of molecules and atoms and these possess kinetic and potential energy as well. 

This microscopic energy that an object or substance will possess is called its Internal Energy.

Return to Menu

Internal Energy (U)

Often we refer to systems and surroundings when we talk about energy. 
  • The system is where the process occurs and
  • everything not in the system is in the surroundings. 
This allows us to account for all the different energy components we are going to discuss. 
 
So, let’s choose our process to be a human body, where the system is the human body and the surrounding is everything around it.
 
Consider the drawing below where I depict a simple idealized molecule consisting of two atoms and a chemical bond between them.
  
Picture: Internal Energy (U) Components 
 
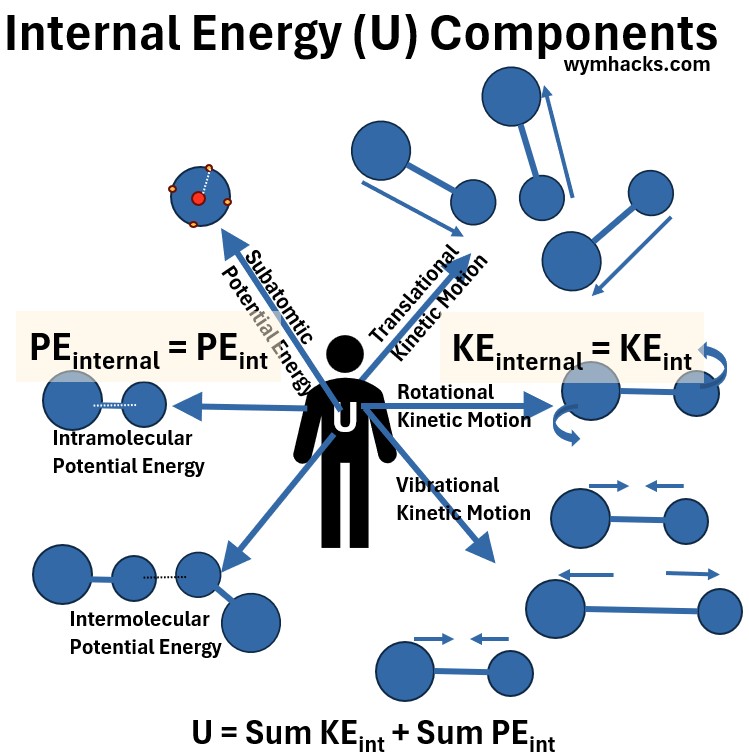
The Internal Energy (U) of this body is the sum of all the atomic and molecular energies that make up the body. 
 
These can be movement (Kinetic) energies like 
  • the bulk motion of molecules (Translational) or
  • the rotational movement of molecules (Rotational) or
  • the vibrational movement of molecules (Vibrational).
The total energy will also include position and configuration (Potential) energies consisting of electromagnetic or strong force attractions among the atoms including
  • atomic nuclear binding forces
  • atomic attractive forces inside (within) the molecules (Intramolecular)
  • atomic attractive forces among or between the molecules(Intermolecular)

We can define U in equation form as

(14) U = ΣKEint  +ΣPEint 

where
  • U = the total Internal Energy
  • ΣKEint  = sum of all Kinetic Energies of the atoms and molecules
  • ΣPEint = sum of all Potential Energies of the atoms and molecules

A few important characteristics of U are:

  • It is a property of the body at
  • any instance in time (instantaneous). 
  • U is therefore a State (or Point) Function. 

Return to Menu

External Energy of a System

We want to ensure we’ve identified all the energies associated with a system. 

Any process (or body or substance etc.) as a whole (i.e. on a macroscopic or bulk scale) will possess

  • Kinetic Energy if it is moving relative to a reference point
  • Potential Energy if is configured or positioned differently than a reference point

These are the same concepts as discussed for internal energy but in this case they are being applied to the system as a whole (macroscopically)

So we can comprehensively define the energy of a system by adding up all its Internal and External energies. 

Picture: A System Can Possess both Internal and External Energies

The total energy of a system in equation form is:

(15) Etot = U + Eext
(16) Etot = U + Eext
(17) Etot = ΣKEint + ΣPEint + KEext + PEext
  • E tot = Total energy of a substance/object/body
  • U = the total Internal Energy
  • ΣKEint  = sum of all Kinetic Energies of the atoms and molecules (internal)
  • ΣPEint = sum of all Potential Energies of the atoms and molecules (internal)
  • KEext = kinetic energy of the system as a whole (bulk, external)
  • PEext = potential energy of the system as a whole (bulk, external)

And just like U, all the other terms above are also an instantaneous properties of the system. 

Return to Menu

1st Law of Thermodynamics for A Closed System

The First Law of Thermodynamics may be stated as follows:
 
Although energy assumes many forms,
  • the total quantity of energy is constant, and
  • when energy disappears in one form,
  • it appears simultaneously in other forms

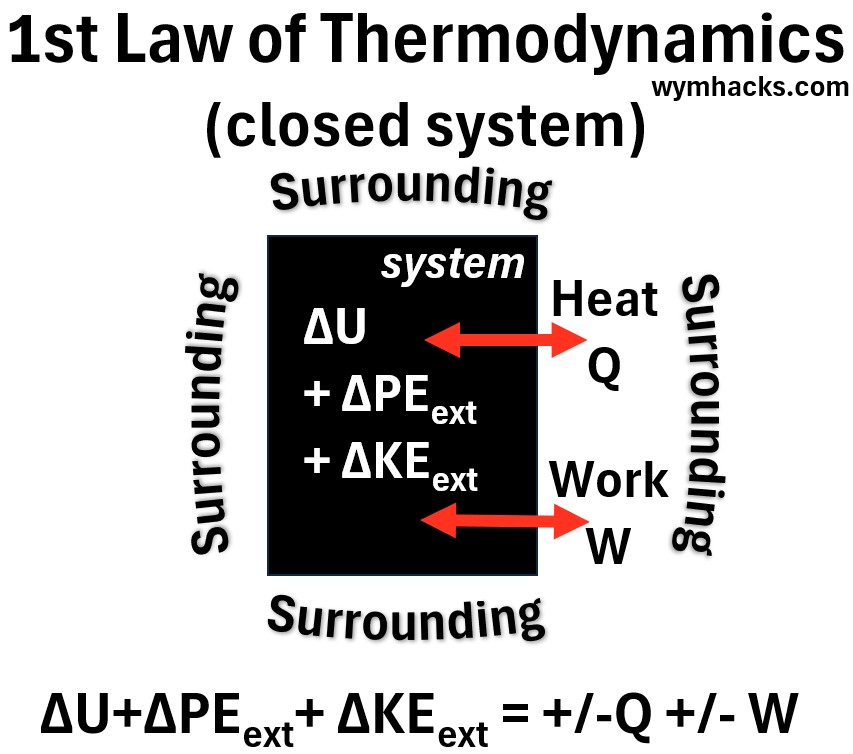
Consider a system represented by the black box in the picture below. 

  • Assume the system is closed meaning the mass is constant (no flow of mass across the boundary).
  • Assume a finite change to the systems energy has occurred. 
Picture: First Law of Thermodynamics – Closed System

Then we can start with equation (17) and state 

The First Law of Thermodynamics for a closed system as:

(18) ΔEtot =ΔΣKEint +ΔΣPEint +ΔKEext +ΔPEext = +-Qnet+- Wnet  (closed system)

where

  • Δ indicates a finite change
  • Qnet  and Wnet are the (cumulative) net heat and work being added or subtracted from the system.
  • A (+) means Q or W is being added to the system (work done to or on system).
  • A (-) means Q or W is being subtracted from the system (work done by system).

I think its clear and logical to use the +/- signage on the right hand side to indicate energy entering (+) or leaving (-) the system. 

Sadly, the most common convention is to show the right hand side as Q – W where +W is interpreted as work being done by the system.

The conventional way is just confusing and and non-intuitive.

It makes more sense to 
  • Write the right hand side as Q + W 
  • then assign the + or – to the Q or W depending on whether its being added (+) or subtracted (-).
  • Any energy or work entering the system will increase the system energy and so should be a positive. 
  • Any energy or work leaving the system will decrease the system energy and so should be a negative.
  • Ill call this the MMS method. 

For example, in the conventional system, the required thinking if you have work being done on the system is:

  • +W is work done by the system, so work done on the system is -W
  • then I must plug it into Q – W = Q–W = Q + W (right result but circuitously derived.
  • Whereas if I use the MMS method, I know work is being done on the system so it has to be positive.
  • So, Q + W is the right set up….done. 

Ok, thanks for letting me rant a little. 

Back to the equation. Take (18) and

  • substitute for U (the internal PE and KE terms)

You get, 

(19) ΔEtot = ΔU  + ΔKEext + ΔPEext = +-Qnet+- Wnet (closed system)

Take (19) and

  • Get rid of the ΔEtot and
  • assume that the system is stationary and the system PEext is negligible. 

You get, 

(20) ΔU  = +-Qnet+- Wnet (closed system) 

or if we understand that Q and W are the culmination of all the work and heat

(21) ΔU  = +-Q+- W (closed system)

where +- indicate whether energy from Q and W are either 

  • increasing (+) the system energy or
  • decreasing (-) the system energy

Conventionally you will see (21) written as

(22) ΔU = Q – W  (closed system)

where

  • Q = heat added to the system
  • W = Work done by the system

Remember that these equations apply only to closed systems where no mass is moving in or out.

The Right Hand Side

The right hand sides of equations (21 or 22) involve energy in transit across the system boundary.

Q and W are not instantaneous properties of the system or surroundings. 

They are energy moving into or out of the system boundary resulting in a quantity that accumulates or dissipates over time. 

These kind of functions are called Path Functions

  • as opposed to the Left Hand Side of the equation
  • which involves State or Point functions.  

A few more comments on heat…

Heat

Heat (Q) is defined as the

  • transfer of energy between a system and its surroundings
  • due to a temperature difference.

In the 1st law equations above, Q is the 

  • heat done by the system on its surroundings (-Q), or
  • heat done by the surroundings on the system (+Q).

Its important for you to understand that heat is not temperature. 

  • Heat is energy in transit due to a temperature difference.
  • Temperature is the driving force for the transfer of energy as heat.
  • The amount of heat transferred is a function of the heat capacity C (specific heat) of a substance and the temperature difference
    • dQ = mCdT , where m is mass, C is specific heat, and T is temperature range
    • Q=mC(T2−T1) , when the specific heat capacity (C) of the substance can be considered constant over the temperature range being considered.
  • Temperature is a State or Point function.
    • It is an instantaneous property (like U).
  • Heat is a quantity and depends on the path taken (Path Function).
  • Heat is energy in transit which takes time and results in the accumulation or loss of energy.
  • The result of heat transfer is a change in the internal energy of the system (which manifests as changes in the kinetic and/or potential energies of the molecules within the system)

When you are holding a cup of warm water, the warmness is a property of the system that is described by temperature. 

  • This cup of water does not have a heat. It has a temperature.
  • The transfer of heat might have caused that temperature but the warmness you feel is the temperature.  

Work

 on the right-hand side of the First Law of Thermodynamics represents

  • work done by the system on its surroundings (-W), or
  • work done by the surroundings on the system (+W).
  • It is a transfer of energy across the system boundary
  • due to a macroscopic force acting through a distance.

This work can exist in various ways. Some examples are:

  • Boundary work (PV work): When a gas expands and pushes a piston, it does work on the surroundings.
    • Force * distance
    • = Force * Volume/Area
    • = Force/Area * Volume
    • = Pressure* Volume
    • = PV work
  • Shaft work: A rotating shaft delivering power out of or into the system.
  • Electrical work: Current flowing through a resistor in the system, or a motor within the system doing work on an external load
  • Other work

Return to Menu

State and Path Functions

I’ve mentioned this a few times but its worth repeating. 

There are two distinct types of terms listed in the 1st Law of Thermodynamics equation. 

  • State (Point) terms (or variables or functions) and
  • Path terms or (variables or functions)

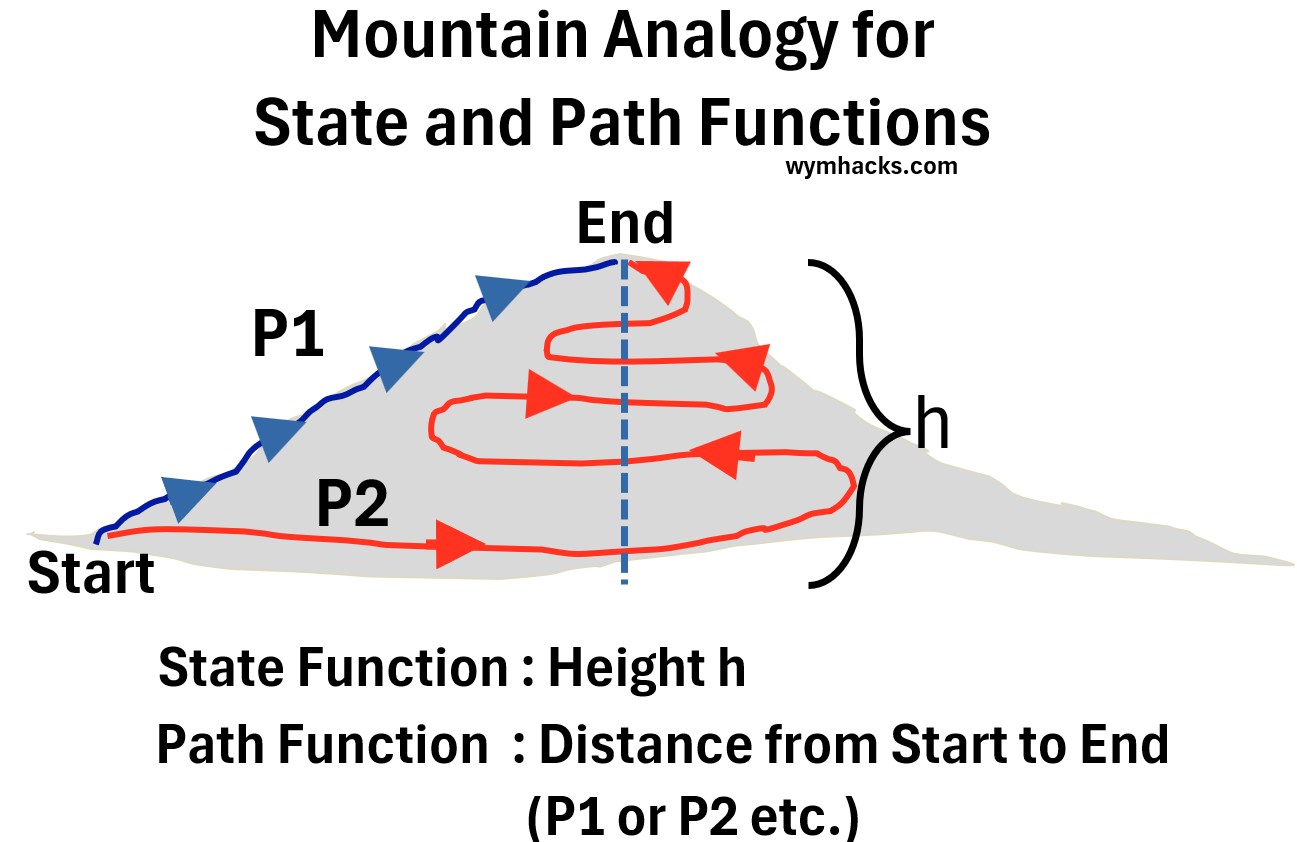
Consider the mountain analogy picture below as you read this section.

Picture: State and Path Functions Mountain Analogy

Recall the 1st Law equation in its full form

(19) ΔU  + ΔKEext + ΔPEext = +-Qnet+- Wnet (closed system)

The terms on the Left hand side (U and the macroscopic movement and position energies of the system as a whole) 

  • are State (or Point) Functions
  • U and the external energies are instantaneous properties of the system.
  • They are instantaneous indicators of the state of the system. 
  • They do not depend on the path taken to get to that point or condition or state.
  • The height of the mountain is a State Function in the mountain analogy picture above. 

The Work and Heat terms on the right hand side, however, 

  • are Path Functions. 
  • Q and W are energies in transit. 
  • They will accumulate or reduce in the system over time. 
  • i.e. they are not instantaneous and depend on the path taken.
  • There is no instantaneous condition or property called heat or work. 
  • The P1 and P2 routes in the mountain analogy picture above produce path functions
    • The distance or energy expended to get to the top are path functions
    • They will be different depending on whether route P1 or P2 is taken. 

The distinction between state and path functions is

  • crucial for applying thermodynamic laws,
  • calculating energy changes, and
  • understanding the efficiency of processes.

Return to Menu

Enthalpy

Enthalpy is always defined as

(23) H = U + PV (any system, always)

where

  • H = Enthalpy
  • U = internal energy
  • P = Absolute pressure
  • V = volume

H, U and PV have units of energy. 

  • PV is energy also because,
  • Force * distance
  • = Force * Volume/Area
  • = Force/Area * Volume
  • = Pressure* Volume
  • = PV

U, P, and V are all State Functions so H is also.

For a finite change the enthalpy equation can be written as: 

(24) ΔH = ΔU + Δ(PV)

Recall the First Law (for closed system, with negligible external system energies)

(21) ΔU  = +-Q+- W (closed system)

Assume heat is added to the system and work is being done by the system

(22) ΔU  = Q – W (closed system)

Substitute (22) into (24)

(25) ΔH = Q – W + Δ(PV)

Assume that only PV work is being considered (e.g. a piston is being moved up by an expanding volume).

(26) ΔH = Q – PΔV + Δ(PV)

Assume constant Pressure.

(27) ΔH = Q – PΔV + PΔV

The last two terms cancel , giving us

(28) ΔH = Q (closed system, PV work only, constant Pressure)

So, given all the assumptions we made are true, the change in enthalpy is exactly equal to the heat transferred.

Return to Menu

Steady State Flow Process

Consider a process depicted in the picture below where

  • conditions within it are constant at all time (steady state) and
  • there is no accumulation of mass or energy in the system
Picture: Steady State Flow Process

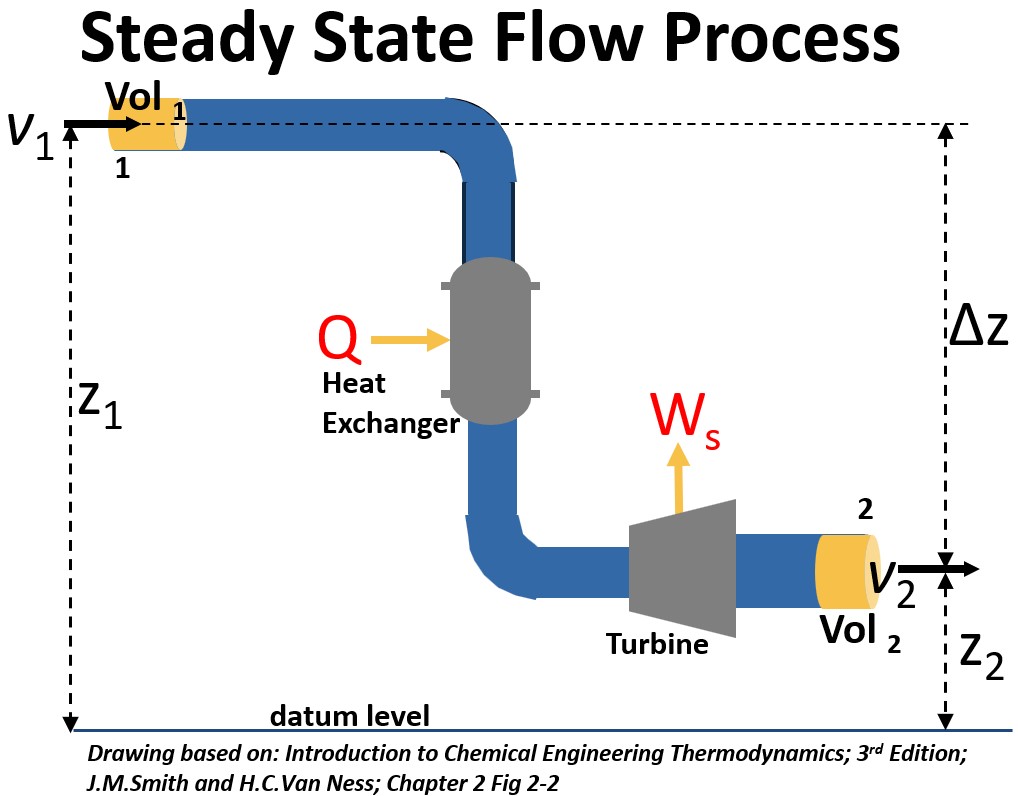
In the diagram above, a fluid flows from the entrance at 1 to the exit at 2.

  • A unit of mass = 1 is flowing
  • Conditions at 1 are
    • elevation from the datum level of z1 
    • velocity v1,
    • volume V1,
    • a pressure P1 and
    • an internal energy U1
  • Conditions at 2 are z2 , v2, V2, P2 , and internal energy U2
  • m1 = m2 = m

Lets apply the First Law of Thermodynamics equation for closed (constant mass) systems:

(19) ΔU  + ΔKEext + ΔPEext = +-Qnet+- Wnet (closed system)

The change in Kinetic Energy of the system from equation (9) is therefore

(29) ΔKEext = 1/2mΔv/gc =1/2(v2-v1)/gc 

where 

  • m = 1 and 
  • the proportionality constant gc is included for those who use English units (lbf and lbm).

The change in the Potential Energy of the system from equation (13) is therefore

(30) ΔPEext = mg/gcΔz =g/gc(z2-z1) 

where

  • m = 1 and 
  • the proportionality constant gc is included for those who use English units (lbf and lbm) and
  • h in equation (13) is replaced with z which is our symbol for height from the datum plane

We can substitute (29) and (30) into (19) and get

(31) ΔU + 1/2Δv/gc  + g/gcΔz  = Qnet+ Wnet (closed system)

where

  • Q and W are the heat and work on a mass = 1 basis (i.e. per unit mass; e.g. energy/mass)

We need to “work” on the Work term now.

There are really two work types that are happening in this steady state system, PV work and Shaft Work. 

  • At the entrance boundary at 1, the fluid is effectively being pushed into the system boundary we’ve defined.
  • So, at entrance 1, work is being done on the system.
    • W1 = Force * distance = F*Volume 1/Area 1 = F*V1/A1 =  F/A1* V1 = +P1V1
  • And, at exit 2, work is being done by the system on the surroundings.
    • W2 = Force * distance = F*Volume 2/Area 2 = F*V2/A2 =  F/A2* V2 = -P2V2
  • We can designate the second kind of work, done by the mechanical turbine, as the shaft Work being done on the surroundings =  – Ws

Let’s put these work terms into equation (31).

(32) ΔU + 1/2Δv/gc +  g/gcΔz  = Q + P1V1 – P2V2 – Ws

Move the PV terms to the left hand side. 

(33) ΔU + P2V2– P1V1 + 1/2Δv/gc +  g/gcΔz  = Q – Ws

Express the PV terms as a Δ (change) expression.

(34) ΔU +Δ(PV) + 1/2Δv/gc +  g/gcΔz  = Q – Ws

Use the enthalpy equation (24) ΔH = ΔU + Δ(PV) to put ΔH into equation (34).

(35) ΔH + 1/2Δv/gc +  g/gcΔz  = Q – Ws (1st Law, Steady State flow process)  

For many applications the kinetic and potential terms can be assumed to be zero. So, 

(36) ΔH = Q – Ws (1st Law, Steady State flow process, negligible KE and PE)

Equations (35) and (36) are commonly used in industry when dealing with steady state flow of fluids through equipment. 

Return to Menu

Deriving Mechanical Energy Equations from The 1st Law

Consider the First Law of Thermodynamics equation that we derived: 
 
(19)  ΔU + ΔKEext + ΔPEext = +-Qnet +- Wnet (closed system)

From my Work and Energy post (go to Mechanical Energy Equations section) we know that

(37) Wnet = Wc + Wnc

Where

Wc  =  Work done by a Conservative Forces (produce path dependent work)

Wnc  =  Work done by Non – Conservative Forces (work is path dependent)

We also know that Wc is equal to the potential energy:  

(38) Wc  = – ΔPE

Substituting for Wnet and Wc  in equation (19) gives

(39) ΔU + ΔKEext + ΔPEext = +-Qnet +-(Wc + Wnc) 
(40) ΔU + ΔKEext + ΔPEext = +-Qnet +-(– ΔPE + Wnc)

assume that the PE from the Wc  is absorbed in the PE term on the left hand side of equation (40).

(41) ΔU + ΔKEext + ΔPEext = +-Qnet +-Wnc

Assuming ΔU and Q are negligible (i.e. go to 0), we get

(42) ΔKEext + ΔPEext =  +-Wnc

If we assume Wnc is = 0, 

(43) ΔKEext + ΔPEext =  0

Note that the “ext” subscript

  • means external or macroscopic or system has a whole.
  • When we talk about mechanical energy equations we are talking about these external type energies.  
  • This differentiates it from the Internal Energy U which is the energy of the atoms and molecules that make up that object. 

(43) is generally called the “Conservation of Mechanical Energy” equation. 

If there are no Non – Conservative forces doing work on an object, its mechanical energy is conserved (i.e. constant).

Return to Menu

Appendix 1 – History Of Energy

  • 1676-1689: Leibniz introduces vis viva (mv2).
  • 1802-1807: Thomas Young introduces the term “energy” to refer to the quantity formerly known as vis viva.
  • 1828-1829:
    • Coriolis formalizes “work” and the 1/2mv2 formula for the energy of motion.
    • Poncelet popularizes these ideas.
  • 1840s-1850s: 
  • 1849-1851: William Thomson (Lord Kelvin) coins the specific term “kinetic energy“.
  • 1853: William Rankine coins the term “potential energy“.

So, while Young coined the general term “energy”, 

  • the specific forms “kinetic energy” and “potential energy” and
  • the comprehensive understanding of energy as a conserved quantity that transforms between these forms,

was the result of the work of many scientists over more than a century. 

Return to Menu

Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for  professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.

Leave a Comment

Your email address will not be published. Required fields are marked *