Menu (linked Index)
Geometry and Trigonometry Rules
Last Update: November 8, 2025
- Introduction
- Area and Volume Equations for Basic Shapes
- Similar Triangles
- Exterior and Interior Angles of Triangles
- Law of Cosines and Sines
- Right Triangle Trigonometric Functions
- Pythagorean Trigonometric Identities
- Sum and Difference Angle Formulas
- Product-to-Sum Formulas
- Even-Odd Identities (Identities for Negative Angles)
- Some Useful Sine and Cosine Equivalence identities
- Derivatives of Trig. Functions
- Circle Properties
- Small Angle Approximations
- Radius of Curvature
- Normal (Perpendicular) Line to Circle Surface
Introduction
This post summarizes some useful geometric and trigonometric functions and rules.
Check out this nice video tutorial :
All the TRIG you need for calculus actually explained – Dr. Trefor Bazett
Areas/Volumes of Basic Shapes
The drawings below were copied from the Wikipedia – Area page.

Square: Area of a Square = s2
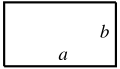
Rectangle: Area of a Rectangle = ab
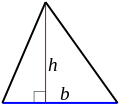
Triangle: Area of a Triangle = (1/2)bh

Parallelogram: Area of a Parallelogram = aha

Trapezoid: Area of a Trapezoid = (a+c)h/2

Circle: Area of a Circle = π r2
Circle: Circumference of a Circle = 2π r
π ∼= 3.14159…

Sphere: Surface Area of a Sphere = 4π r2
Sphere: Volume of Sphere = (4/3)π r3
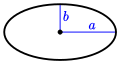
Ellipse: Area of an Ellipse = πab
Similar Triangles
Similar Triangle geometry: If two triangles are similar, then their corresponding angle measures are equal , and their corresponding side lengths are in the same ratio.
So for Similar Triangles ABC and DFE:
θ1=θ7 ; θ2=θ8 ; θ3=θ9
and
b/f = a/d = c/e
Exterior and Interior Angles of a Triangle
Exterior Angle Geometry: When a triangle’s side is extended, the resultant exterior angle formed is equal to the sum of the measures of the two opposite interior angles of the triangle:
So for Triangle ABC:

θ6 =θ1+ θ2
θ5= θ3 +θ1
θ4 =θ3 +θ2
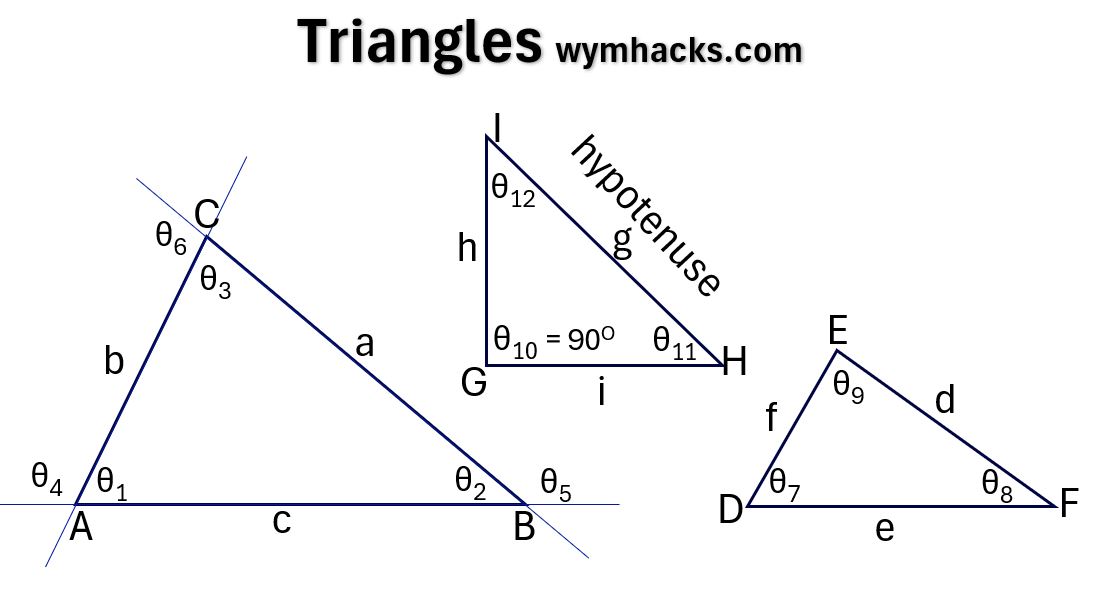
Law of Cosines and Law of Sines
Law of Sines
a/sin(A) = b/sin(B) = c/sin(C) ; Law of Sines
Picture: Law of Sines Triangle
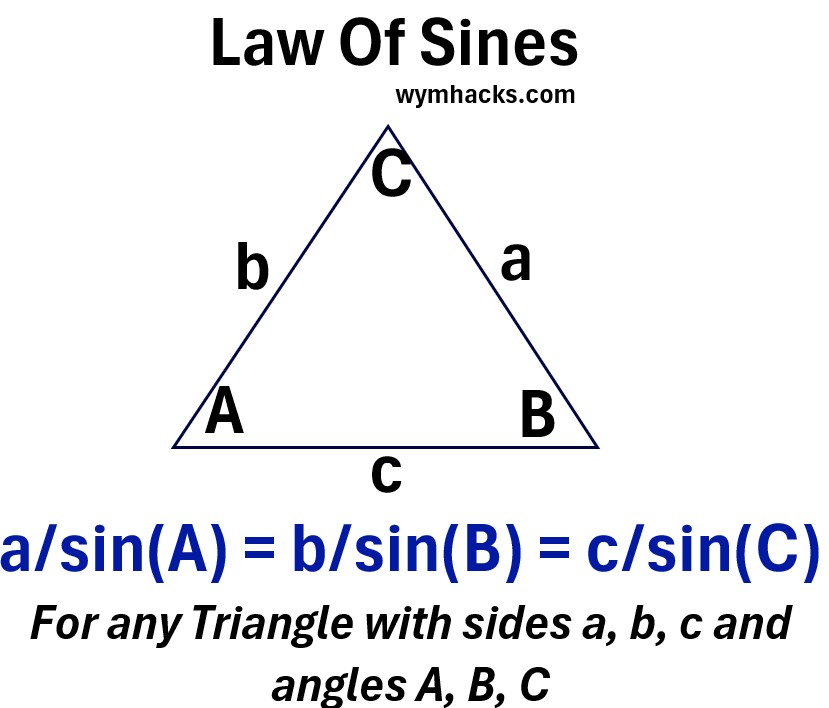
Law of Cosines
a2= b2+c2 – 2bccos(A) ; Law of Cosines
b2= a2+c2 – 2accos(B) ; Law of Cosines
c2= a2+b2 – 2abcos(C) ; Law of Cosines
Picture: Law of Cosines Triangle
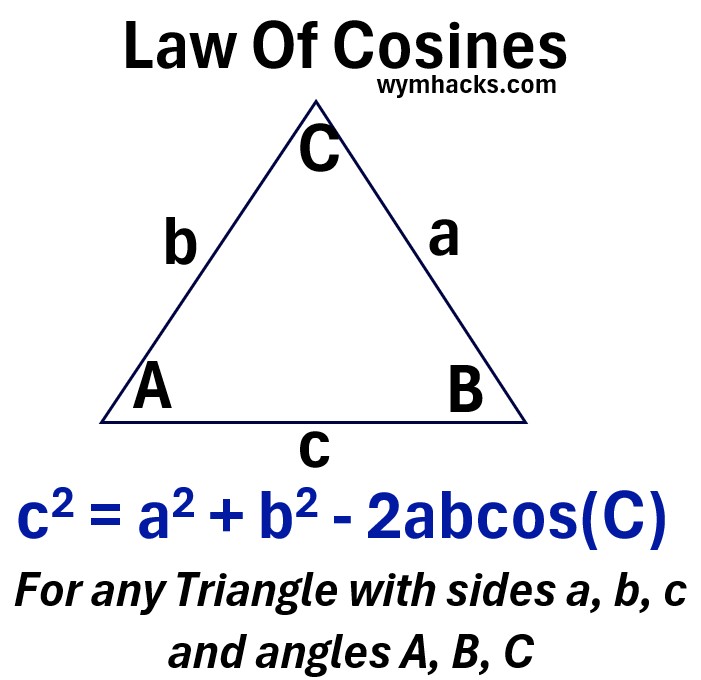
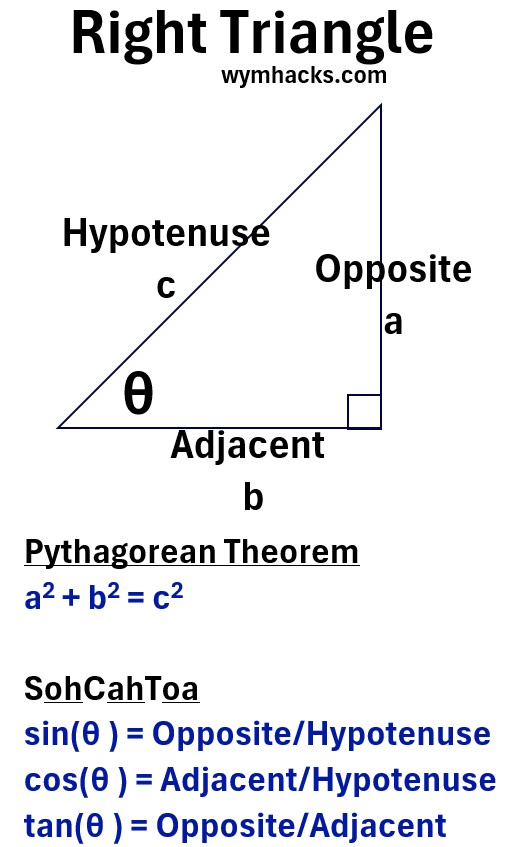
Right Triangle Trig Functions
For a right triangle as shown below:
Pythagorean Theorem: a2 + b2 = c2
sin(θ) = opposite/hypotenuse
cos(θ) = adjacent/hypotenuse
tan(θ) = opposite/adjacent = (hypotenuse)(sin(θ))/(hypotenuse)(cos(θ)) = sin(θ)/cos(θ)
mnemonic: SohCahToa
Pythagorean Identities
From the Pythagorean theorem we know that
- a2 + b2 = c2
- sin(θ) = a/c
- cos(θ) = b/c
- tan(θ) = a/b
Divide Equation 1 by c2
a2/c2+ b2/c2= c2/c2
Simplify and substitute using 2. and 3. to get
sin2(θ) + cos2(θ) = 1 ; Pythagorean Identity
Divide equation 1 by a2
a2/a2+ b2/a2= c2/a2
Simplify and substitute in 4. and 2. to get
1+ 1/tan2(θ) = 1/sin2(θ)
or
1+ cot2(θ) = csc2(θ) ; Pythagorean Identity
Divide equation 1 by b2
a2/b2+ b2/b2= c2/b2
Simplify and substitute in 4. and 3. to get
tan2(θ)+ 1 = 1/cos2(θ)
or
1+ tan2(θ) = sec2(θ) ; Pythagorean Identity
These identities are always true.
For completeness, let’s prove that in the next section.
Derivation of Trig Identities from a Unit Circle
Consider a unit circle with a radius of 1 centered at the origin (0,0):
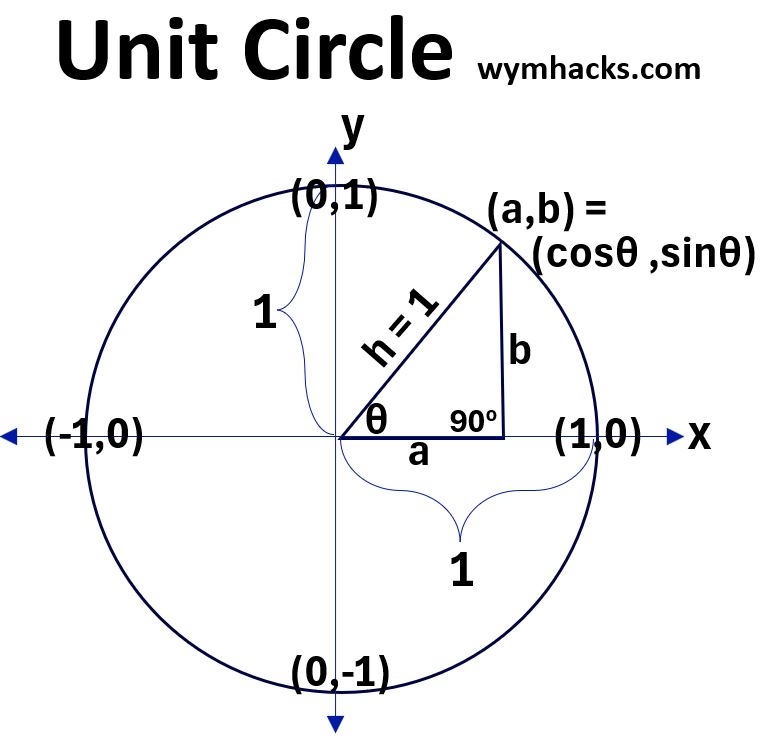
On a unit circle, by definition, every point on the circumference will have coordinates (a,b) = (x,y) = (cosθ,sinθ)
x = cosθ
y = sinθ
The equation for the unit circle is
x2 + y2 = 1
So , substituting for x and y we get
cos2θ + sin2θ = 1 ; Pythagorean Identity
Divide “cos2θ + sin2θ = 1″ by cos2θ to get
cos2θ /cos2θ+ sin2θ/cos2θ = 1/cos2θ
or
1 + tan2θ = sec2θ ; Pythagorean Identity
Divide “cos2θ + sin2θ = 1″ by sin2θ to get
cos2θ /sin2θ+ sin2θ/sin2θ = 1/sin2θ
or
cot2θ + 1 = csc2θ ; Pythagorean Identity
Sum and Difference Angle Formulas
These trig identities can come in useful (solving integrals, etc.).
They can be derived from applying basic trig and geometry to two right triangles.
You can see the detailed derivation in my post: Sum and Difference Angle Formula Proofs
sin(α + β) = sinα cosβ + cosα sinβ
sin(α – β) = sinα cosβ – cosα sinβ
cos(α + β) = cosα cosβ – sinα sinβ
cos(α – β) = cosα cosβ + sinα sinβ
tan(α + β) = (tanα + tanβ) / (1 – tanα tanβ)
tan(α – β) = (tanα – tanβ) / (1 + tanα tanβ)
Product-to-Sum Formulas
The product-to-sum trigonometric identities convert a product of sine or cosine functions into a sum or difference of sine or cosine functions.
These identities are derived from the angle sum and difference formulas.
Sine times Sine
The product of two sines is converted to a difference of cosines:
sin(mx)sin(nx) = 1/2[cos(mx – nx) – cos(mx + nx)]
or
sin(mx)sin(nx) = 1/2[cos((m-n)x) – cos((m+n)x)]
Cosine times Cosine
The product of two cosines is converted to a sum of cosines:
cos(mx)cos(nx) = 1/2[cos(mx – nx) + cos(mx + nx)]
or
cos(mx)cos(nx) = 1/2[cos((m-n)x) + cos((m+n)x)]
Sine times Cosine
sin(mx)cos(nx) = 1/2[sin((m+n)x) + sin((m-n)x)]
Cosine times Sine
cos(mx)\sin(nx) = 1/2[sin((m+n)x) – sin((m-n)x)]
Even-Odd Identities (Identities for Negative Angles)
cos(−a) = cos(a) ; The cosine function is even.
- The cosine function is even because the sign of the angle doesn’t change the value of the function.
sin(−a)=−sin(a); The sine function is odd.
- The sine function is odd because it is symmetric about the origin, meaning the function value flips its sign.
tan(−a)=−tan(a); The tangent function is odd like the sine function
- The tangent function is odd because it is a quotient of an odd and an even function (sin(a)/cos(a))
Useful Cosine and Sine Equivalence Identities
cos(-θ) = cos(θ)
cos(θ + π/2) = -sin(θ)
cos(θ – π/2) = sin(θ)
cos(π/2 – θ) = sin(θ)
sin(-θ) = -sin(θ)
sin(θ + π/2) = cos(θ)
sin(θ – π/2) = -cos(θ)
sin(π/2 – θ) = cos(θ)
Derivatives of Trig Functions
Derivatives of sin(x) ,cos(x) , tan(x), cot(x), sec(x), csc(x)
- d/dx(sinx) = cosx
- d/dx(cosx) = -sinx
- d/dx(tanx) = sec2x
- d/dx(cscx)=−cscxcotx
- d/dx(secx)=secxtanx
- d/dx(cotx)=−csc2x
- !! These derivatives are only true if x is in units of Radians i.e. not degrees. (due to the limit assumptions made in the derivations).
Circle Properties
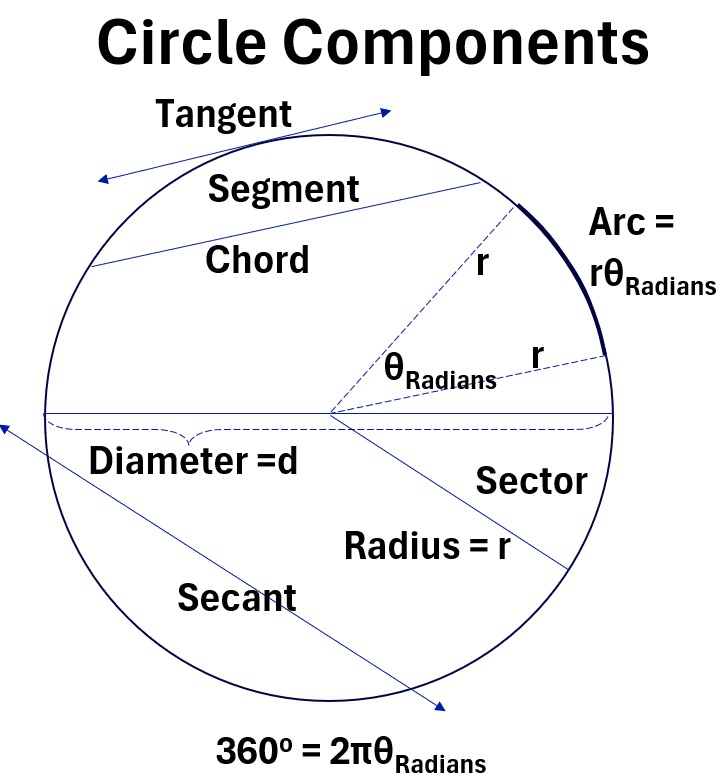
Area of a Circle = πr2
Circumference of a Circle = 2πr
π ∼= 3.14159…
A radian is the angle subtended at the center of a circle by an arc that has a length equal to the circle’s radius.
- Arc length = rθRadians
- One complete revolution around a circle is equal to 2π radians,
- which is also equal to 360 degrees.
- Therefore, 1 radian is approximately 57.3 degrees.
Small Angle Approximations
Small angle geometry: If angle θ is small,
sin(θ) ≈ θ
cos(θ) ≈ 1 – θ2/2 ≈ 1
tan(θ) ≈ θ
Radius of Curvature
Circle geometry: Consider the drawing below comparing the red shaded (flat) curve with the blue (steep) shaded curve.
If we fit a circle to each curve, we get the two circles shown in the drawing below.
Picture_Radius of Curvature of a Curve
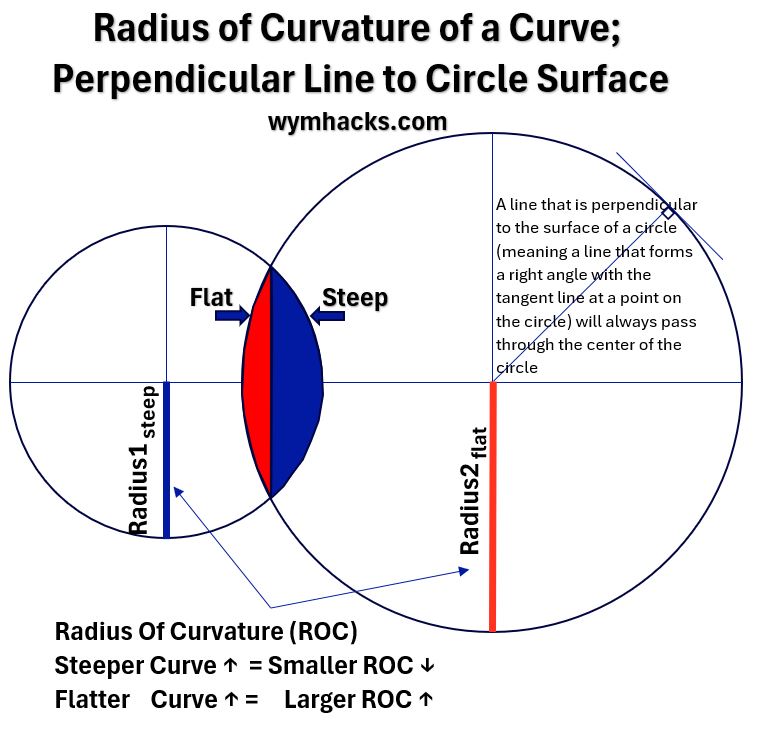
The Radius of Curvature for each curve is the radius of the fitted circle.
- The Radius of Curvature of the red curve is longer. The red curve , relative to the blue curve, is described as being “flat”.
- The Radius of Curvature for the blue curve is shorter. The blue curve , relative to the red curve, is described as being “steep”.
If the curves are not perfectly spherical, the same concept is applied but the Radius of Curvature could vary from point to point on the surface.
With respect to lenses, the focal length (distance between the focal point and the optical center) of the lense will be proportional to the Radius of Curvature.
- A lens with A longer focal length will focus light rays to a point further away from the lens (and vice versa).
- For a spherical lens, the focal length is approximately half the radius of curvature of the lens surface.
- The above relationship holds true when the lens is thin compared to its radius of curvature.
- For non-spherical lenses, the relationship between focal length and Radius of Curvature is more complex.
Perpendicular Line to the Surface of a Circle
Circle geometry: Since we have a nice drawing of a circle above, we can also define the normal line or perpendicular line to the surface of a circle:
A line that is perpendicular (normal) to the surface of a circle (meaning a line that forms a right angle with the tangent line at a point on the circle) will always pass through the center of the circle.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.