Menu (linked Index)
Rotational Motion Variables
Last Update: October 28, 2025
Introduction
This post addresses rotational (circular) motion and the key variables describing it.
We are probably familiar with linear movement described by position x, velocity v, and acceleration a, but describing things that rotate requires a new set of variables:
- angular position θ,
- angular velocity ω,
- and angular acceleration α.
These rotational variables are intrinsically linked to their linear counterparts (v and a) by the radius r of the object’s path.
Understanding this relationship—how r connects the spinning motion to the straight-line speed—is key to mastering circular physics.
I used these very helpful sources to write this article:
- University Physics Volume 1; 10.1 Rotational Variables
- Circular Motion Everything You Need To Know! Brain Station Advanced
- Angular motion variables
- Relating angular and regular motion variables
- Introduction to rotational motion review
- Rotational kinematic formulas
- Angular kinematics review
- UP1 (9C) Rotational variables- Learn Physics with Dr. Viv!
- Google Gemini
Angular Displacement and Radian Definition
Consider rotational (circular) motion of a point on the circumference of a circle on the xy plane as shown in the picture below.
Rotational (Circular) Motion: Arc Length ; s
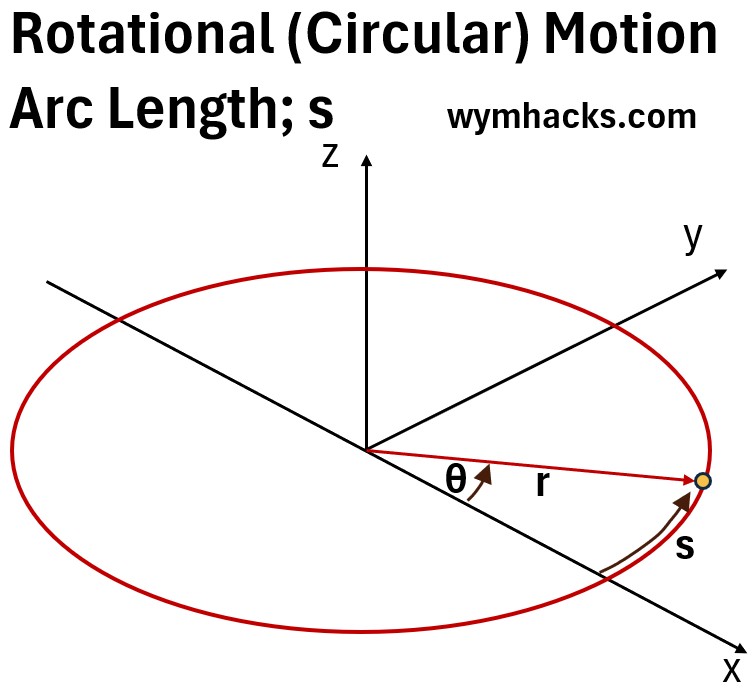
- The point is travelling along the arc “s” from the positive x axis and moving counterclockwise.
- The position vector r represents the position of the point on the circumference of the circle relative to the circle center (origin).
Let θ be the angle that subtends the arc “s”.
- We’ll call it angular position or
- angular displacement when seen as a movement from an initial position to a final position.
By definition,
(1) θ = s/r or s = r θ ; Angular position in radians (rad)
- The radian is a ratio of lengths so it is dimensionless (even though we say it has units of radians).
- When θ = 1 rad, the length of the arc subtended by it is equal to the radius
- 1 radian = 57.296° (degrees)
- π radians = 180° and 2π radians = 360°
Angular Velocity ω
Angular velocity ω is the rate of change of angular displacement with respect to time.
The average magnitude of angular velocity = ω = ∆θ/∆t in radians/s = rad/s
(2) ω = ∆θ/∆t in radians/second (rad/s); Average magnitude of angular velocity
Using finite quantities like ∆θ/∆t calculates the average angular velocity, which is an approximation of the rotation across a measurable time interval.
By contrast, using differentials (e.g. dθ/dt) calculates the instantaneous angular velocity by finding the rate of change as the time interval approaches zero, providing the exact rotational speed at a single instant.
This is crucial because it allows for the accurate modeling and calculations in real-world, non-uniform rotational motion.
So let’s use the instantaneous (infinitesimal) equivalent for ω (as time goes towards zero):
(3) ω (∆t -> 0) = dθ/dt; Instantaneous magnitude of angular velocity
We want to now take the time derivative of “s” using equation (1) θ = s/r or s = r θ :
(4) ds/dt = d/dt(rθ) = θdr/dt + rdθ/dt
where we’ve used the differentiation product rule (see my post: The Derivative ).
We know (or assume) that:
- r is constant, so dr/dt = 0
- ds/dt = vt = magnitude of the tangential velocity (i.e. speed) of a point on the circumference
- dθ/dt = ω = magnitude of the angular velocity (equation (3))
So, equation (4) becomes
(5) vt = ωr; Magnitude of the tangential velocity (speed)
Equation (5) states that the tangential speed of the particle is its angular velocity ω times the radius of the circle.
It tells you that, for a constant angular velocity ω, the tangential speed of the particle increases with its distance from the axis of rotation.
vt and ω have both magnitude and direction so they can be expressed as vectors.
(6) vt = ω x r ; Tangential velocity vector
- The tangential velocity vt is the cross product of the angular velocity vector ω and the position vector r
- Using the right hand rule (explained below) , vector ω points up the z axis with counterclockwise motion and
- points down the z axis with clockwise motion.
A picture is worth a thousand words, so take a look below at the circular motion of a point in the xy plane of a cartesian coordinate system.
Picture: Rotational Motion; Angular Velocity ω
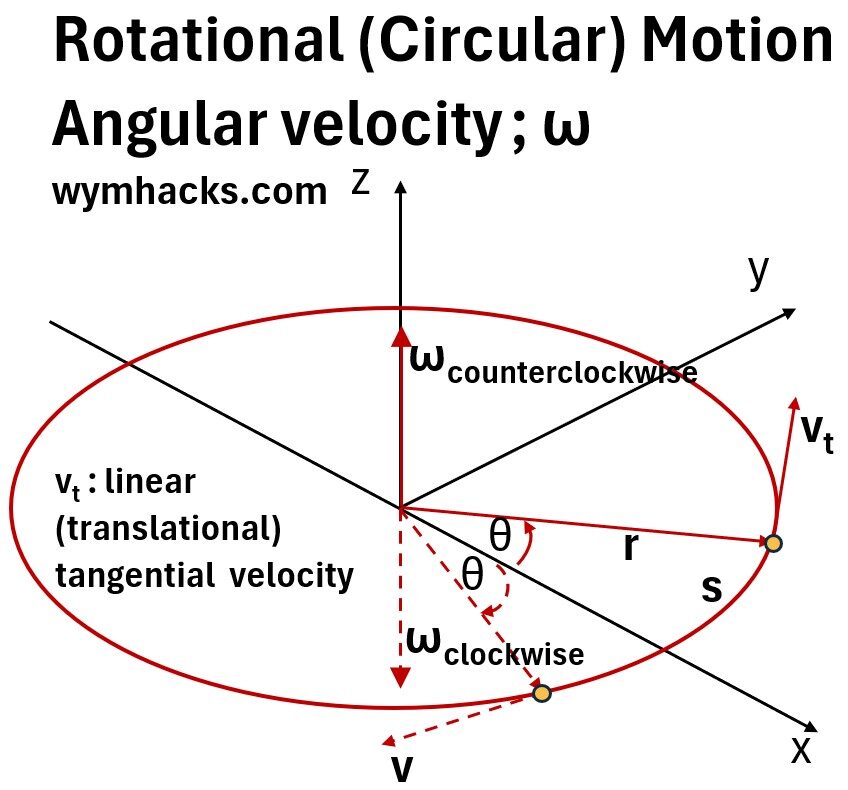
- The angular velocity vector ω points along the axis of rotation (the z axis).
- This is useful because when a body is rotating, we want to know both the axis of rotation and the direction that the body is rotating about the axis, clockwise or counterclockwise.
- The angular velocity ω has a direction determined by the right-hand rule.
- The right-hand rule: Wrap right hand fingers in direction of motion and thumb will point in direction of vector ω
- So ω points up for counterclockwise motion and the opposite way for clockwise motion.
Picture: Right Hand Rule
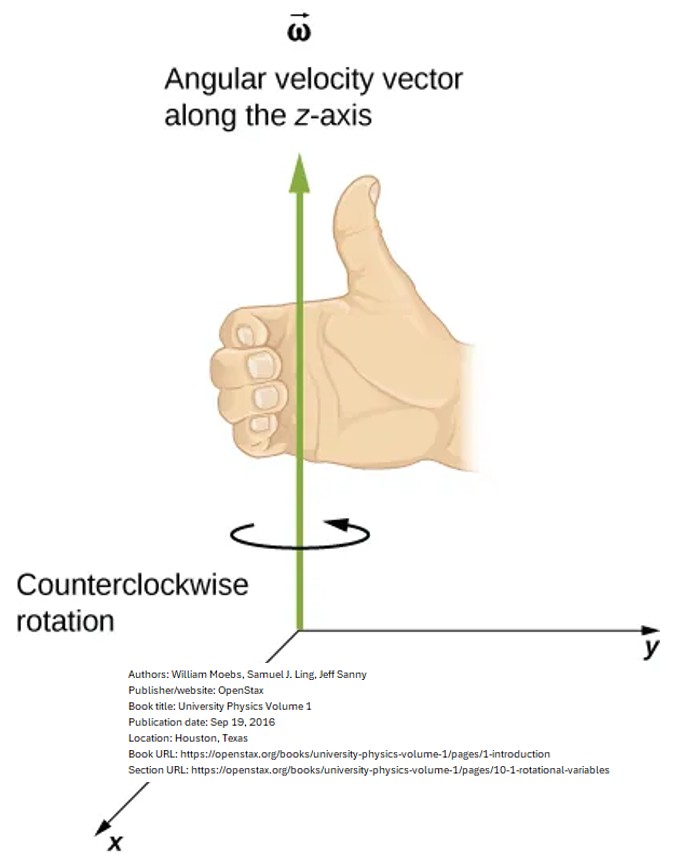
- The tangential velocity vector vt moves in the direction of rotation and is perpendicular to both the position vector r and the angular velocity vector ω
- The cross product equation (6) vt = ω x r tells us this by definition (see my post Vector Math)
- Using the cross product right hand rule (see this video by Physics Peer), we can determine the direction of vt
- Right Hand, fingers/palm open palm, fingers up towards ω direction
- Direction of palm is direction of r
- Thumb direction is vt
Finally, notice that we can derive equation (5) from (6) (see my post Vector Math):
- eq (6): vt = ω x r
- magnitude of vt = |vt| =|ω||r|sin (90°) = wr
- eq (5): vt = wr
Now let’s explore angular acceleration, the rate of change of angular velocity with respect to time.
Angular and Linear Acceleration
Angular acceleration α is the rate of change of angular velocity with respect to time.
The average magnitude of angular acceleration = α = ∆ω/∆t in radians/s/s = rad/s2
(7) α = ∆ω/∆t (rad/s2); Average magnitude of angular acceleration
Let’s use the instantaneous (infinitesimal) equivalent for α (as time goes towards zero):
(8) α (∆t -> 0) = dω/dt; Instantaneous Magnitude of Angular Acceleration
Note that dω/dt = d2θ/dt2
We want to now take the time derivative of “vt” using equation (5) vt = ωr
(9) dvt/dt = d/dt(ωr) = rdω/dt + ωdr/dt
where we’ve used the differentiation product rule (see my post: The Derivative ).
We know (or assume) that:
- r is constant, so dr/dt = 0
- dvt/dt = at = magnitude of the tangential acceleration of a point on the circumference
- dω/dt = α = magnitude of the angular acceleration (equation (8))
So, equation (9) becomes
(10) at = αr ; magnitude of the tangential acceleration
Equation (10) states that the tangential acceleration of the particle is its angular acceleration α times the radius of the circle r.
at and α have both magnitude and direction so they can be expressed as vectors.
(11) at = α x r ; tangential acceleration vector is the cross product of α and r
- The tangential acceleration at is the cross product of the angular acceleration vector α and the position vector r
Lets take a look at how these variables look on a 3D cartesian picture.
Picture: Rotational Motion; Angular Acceleration α
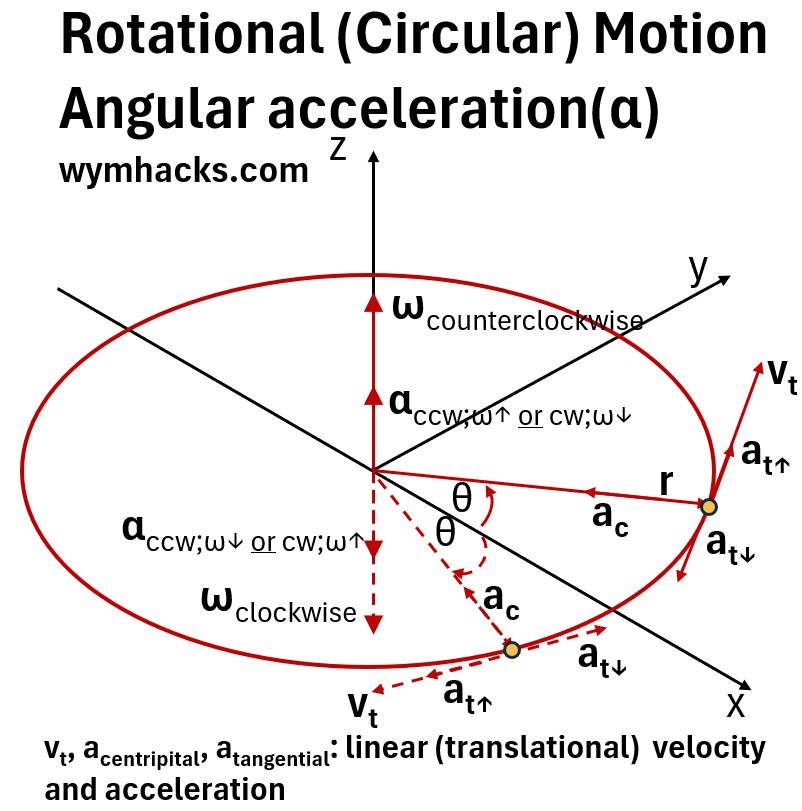
Angular and Linear Acceleration
- The angular acceleration vector α is on the z axis (like ω, the angular velocity vector)
- The angular acceleration vector α points up on the z axis
- with counterclockwise motion and ω increasing or
- with clockwise motion and ω decreasing
- The angular acceleration vector α points down on the z axis
- with counterclockwise motion and ω decreasing or
- with clockwise motion and ω increasing
- The tangential acceleration at vector points in the same direction as the tangential velocity vector vt if w is increasing
- The tangential acceleration at vector points in the opposite direction of the tangential velocity vector vt if w is decreasing
- The centripetal acceleration vector = ac = ω x vt
- |ac| =|ω||vt|sin90 = ωvt
- but vt = ωr from equation (5)
- ac =ωvt = ωωr = ω2r = (vt)2
- The centripetal acceleration vector ac always points inward toward the center of the circle.
- at = α x r is the tangential acceleration component of the total acceleration atot
- atot = (α x r) + (ω x vt ) = at + ac
- Although not shown in the picture above, the vector atot would be located between at and ac, pointing inward (simple vector addition).
Cross Product Right Hand Rule
- Use the cross product right hand rule, to determine the direction of the cross product vectors
- For a = b x c
- Right Hand, fingers/palm open, fingers towards b direction
- Direction of open palm is direction of c
- Thumb direction is direction of a
Derivation of Scalar Equations from Vector Cross Products
Note that we can derive equation (10) from (11) (see my post Vector Math):
- eq (11): at = α x r
- magnitude of at = |at| =|α||r|sin (90°) = αr
- eq (10): at = αr
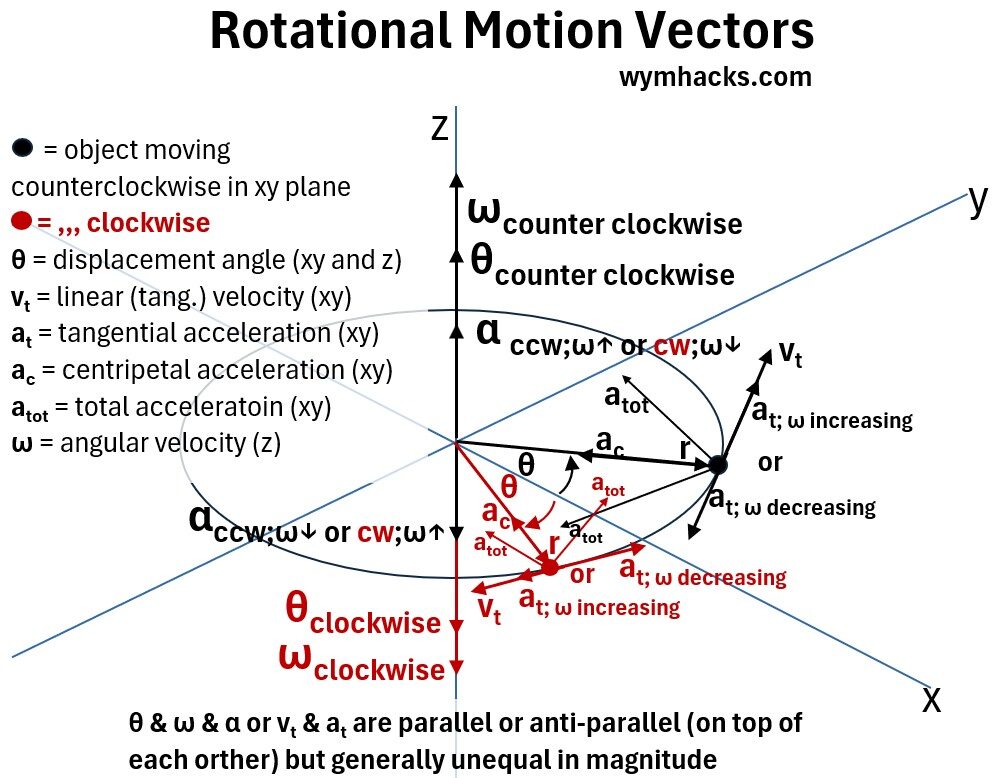
Rotational Motion Vectors
A rendering of all the key vectors related to rotational motion are shown in the picture below.
Notice that I show θ as a vector both in the xy plane and on the z axis.
- This assumption is only valid for infinitesimal changes which I will discuss in the next section.
Picture: Rotational Motion Vectors: Detailed
Notice that
- while the linear acceleration vector has two components (atot = at + ac) the tangential velocity vt does not.
- the linear acceleration and velocity vectors are in the xy plane while the rotational vectors ω, α, θ are perpendicular to them on the z axis.
- the tangential acceleration at points in the direction of vt when ω is increasing and points in the opposite direction when ω is decreasing.
- the angular acceleration vector α points along the z-axis (up or down) based on two factors: the direction of rotation and whether the rotation is speeding up or slowing down.
- Counter-Clockwise / Speeding Up / ω vector on z pointing up/ α vector on z pointing up
- Counter-Clockwise / Slowing Down / ω vector on z pointing up/ α vector on z pointing down
- Clockwise / Speeding Up /ω vector on z pointing down/ α vector on z pointing down
- Clockwise / Slowing Down / ω vector on z pointing down/ α vector on z pointing up
- Speeding Up or Slowing Down means: both the linear and angular components of its motion are increasing/decreasing in magnitude.
- We have angular components (θ, ω, α) and related linear components (r, v, and a)
- which are perpendicular to each other
- suggesting there is a cross product relationship (there is). (see my post: Vector Math)
Deriving the Key Rotational Equations From their Vectors
We can derive our key rotational equations using cross product relationships.
Lets start with the angular displacement θ (or Δθ ).
Picture: Rotational Motion Angular Displacement θ
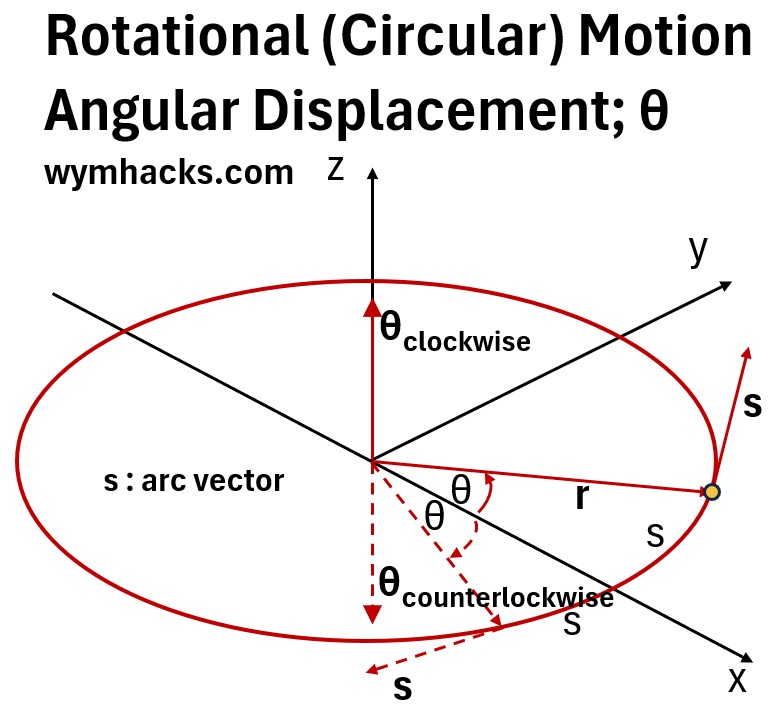
Assume the arc vector s is the cross product of θ and r:
s = θ x r
- take the differential of s with respect to t
- ds/dt = dθ/dt x r + dr/dt x θ
- We’ve used the Differentiation Product Rule specifically adapted for the cross product of two vectors.
- see my post: The Derivative
- see my post: Vector Math
- for fixed r, dr/dt = 0, so the second term drops out
- ds/dt = dθ/dt x r
- ds/dt = vt and dθ/dt = ω so,
- vt = ω x r
- taking the magnitude of both sides we get
- |vt| = |ω||r|sin(90) = v = ωr
vt = ωr ; magnitude of tangential velocity (tangential speed)
Starting with vt = ω x r:
- take the differential of v with respect to t
- dvt/dt = dω/dt x r + dr/dt x ω
- for fixed r, dr/dt = 0, so second term drops out
- dvt/dt = dω/dt x r
- dvt/dt = at and dω/dt = α so,
- at = α x r
- |at| = |α||r|sin(90) = a = αr
- at = αr ; magnitude of tangential acceleration
Kinematic Equations
See my post: Work and Energy where I develop the linear Kinematic equations.
It’s easy to develop the rotational kinematic equations from the linear ones by just dividing by the radius r.
(12a) vf =vi + at ; Linear Kinematic Equation
- Divide by radius r
- vf /r = vi /r + at/r
- vf /r = ωf
- vi /r = ωi
- at/r =αt
(12b) ω = ω0 + αt ; Rotational Kinematic Equation
(13a) d = (1/2)(vi +vf)t ; Linear Kinematic Equation
- Divide by radius r
- d/r = (1/r)(1/2)(vi +vf)t
- d/r = s/r = θ,
- v/r = ω,
(13b) θ – θi = (1/2)(ωi + ω)t ; Rotational Kinematic Equation
(14a) d=vit + (1/2)at2 ; Linear Kinematic Equation
- Divide by radius r
- d/r=(1/r)vit + (1/r)(1/2)at2
- d/r = s/r = θ,
- v/r = ω
- a/r = α
(14b) θ = θ0 + ω0t + 1/2αt2 ; Rotational Kinematic Equation
(15a) (vf2-vi2) = 2ad ; Linear Kinematic Equation
- Divide by radius r
- v/r = ω
- a/r = α
(15b) ω2– ωi2 = 2α(θ – θi) ; Rotational Kinematic Equation
These Kinematic Equations apply only to constant acceleration.
Variables:
- d; di = final and initial displacement
- v; vi = final and initial velocity
- a = acceleration (constant)
- ω; ωi = final and initial angular velocity
- α = angular acceleration (constant)
- θ; θi = final and initial angular displacement
Polar Vectors vs Axial Vectors (Pseudo Vector)
I’ve included this section for completeness.
Since it’s not really a primary focus of this article, you’ll have to do your own research to dig into the topic. (It might confuse the shit
I used Google Gemini to give me a succinct summary of these definitions.
The difference between polar vectors (or “true vectors”) and pseudovectors (or “axial vectors”) lies in how they transform under an improper rotation, specifically a spatial inversion or reflection of the coordinate system.
What is Spatial Inversion?
- A spatial inversion or parity transformation is a fundamental operation in physics and mathematics that reverses the direction of all three spatial coordinate axes.
- It is essentially a specific type of reflection: a reflection through the origin of the coordinate system
Polar Vectors
- A Polar Vector is a vector that is a straight-line displacement or relates to a force/motion along a direction.
- Transformation: Under a coordinate inversion (e.g., (x, y, z) \to (-x, -y, -z) or a mirror reflection),
- a polar vector reverses its direction (it flips sign).
- Why “Polar”? The name is less about poles and more about representing a direction or displacement that extends from a point (like a position vector r in a straight line.)
- Rotational Examples: Position Vector r , Linear Velocity v, Linear Momentum and Force.
Pseudo Vectors (Axial Vectors)
- Axial Vectors are a vector-like quantity associated with rotation or a directional loop.
- They are typically defined using the cross product of two polar vectors
- Transformation: Under a coordinate inversion (reflection), a pseudovector retains its direction (it does not flip sign),
- because the two polar vectors in the cross product both flip sign, which cancels out (-A x – B = A x B).
- Why “Pseudo/Axial”?
- They are called pseudo because they look and behave like vectors under normal rotation/translation, but fail the test of reflection.
- They are called axial because they are always directed along the axis of rotation.
- Rotational Examples: Angular Velocity ω, Angular Acceleration α, Angular Momentum, Torque, Magnetic Field.
The Curious Case of Angular Displacement
Finite angular displacement Δθ is NOT a vector because it fails the fundamental test of vector addition: commutativity (e.g. for vectors, A + B + C = A + C + B; i.e. order does not matter).
Δθ has magnitude and direction but does not obey vector addition rules.
Usually a book rotation analogy is provided to show the violation of this law.
- If you take a book and rotate it 90 degrees on its y axis and then rotate it around the z axis by 90 degrees,
- the final orientation will not be equal to rotating this book first from the z axis and then the y axis.
Infinitesimal angular displacement , dθ, is a vector because when rotations are extremely small, the order in which they are added does not matter (they commute).
This is what allows angular velocity ω to be a true vector derived from dθ (ω = dθ/dt).
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.