Menu (linked Index)
Sum and Difference Angle Formula Proofs
Last Update: October 7,2025
Introduction
In this post, I derive the sine, cosine, and tangent sum and difference angle formulas.
The sum and difference angle formulas are some of the most powerful tools in trigonometry.
While they’re often used to find the exact values for unusual angles like 75∘ or 15∘, their deeper power lies in rewriting expressions—a crucial skill in higher mathematics.
These formulas directly lead to the double-angle identities, which in turn are algebraically rearranged to create the vital Power-Reduction Formulas.
For instance, the identity cos2(x) =1/2(1+cos(2x)) reduces the square of a cosine to a linear form, making it significantly easier to integrate in Calculus.
Sum and difference angle formulas are also used to
- derive the half-angle formulas,
- verify complex trigonometric identities in proofs, and
- solve a wide variety of trigonometric equations.
The Equations
- sin(α + β) = sinα cosβ + cosα sinβ
- sin(α – β) = sinα cosβ – cosα sinβ
- cos(α + β) = cosα cosβ – sinα sinβ
- cos(α – β) = cosα cosβ + sinα sinβ
- tan(α + β) = (tanα + tanβ) / (1 – tanα tanβ)
- tan(α – β) = (tanα – tanβ) / (1 + tanα tanβ)
To memorize the sine and cosine identities think of them as follows:
sin(α ± β) = sinα cosβ ± cosα sinβ
cos(α ± β) = cosα cosβ ∓ sinα sinβ
Good References
Trigonometry Review
We’ll need to remember some trigonometry so here is your relevant review.
Refer to my post Geometry and Trigonometry Rules for more details.
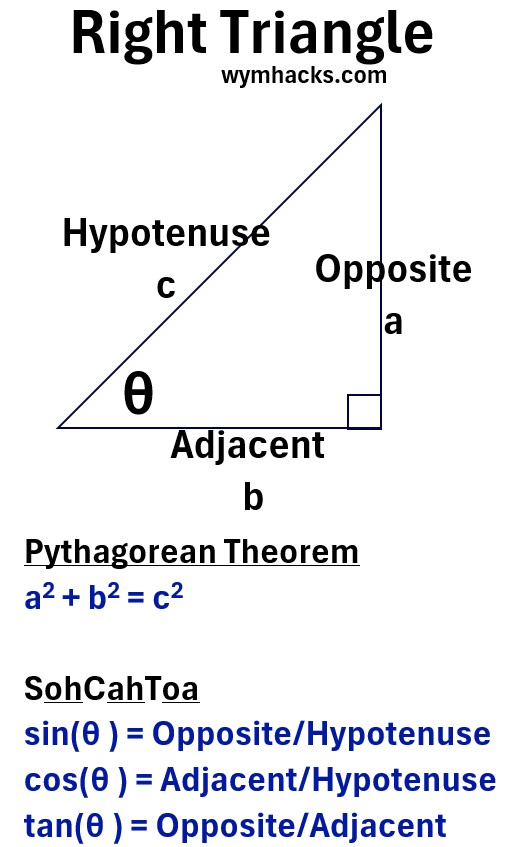
Right Triangle Rules
For a right triangle as shown below:
Pythagorean Theorem: a2 + b2 = c2
sin2(θ) + cos2(θ) = 1 ; Pythagorean Identity
sin(θ) = opposite/hypotenuse
cos(θ) = adjacent/hypotenuse
tan(θ) = opposite/adjacent = (hypotenuse)(sin(θ))/(hypotenuse)(cos(θ)) = sin(θ)/cos(θ)
mnemonic: SohCahToa
Even-Odd Identities (Identities for Negative Angles)
cos(−a) = cos(a) ; The cosine function is even.
- The cosine function is even because the sign of the angle doesn’t change the value of the function.
sin(−a)=−sin(a); The sine function is odd.
- The sine function is odd because it is symmetric about the origin, meaning the function value flips its sign.
tan(−a)=−tan(a); The tangent function is odd like the sine function
- The tangent function is odd because it is a quotient of an odd and an even function (sin(a)/cos(a))
Two Right Triangles
The proof for the sum and difference angle formulas comes from constructing two right triangles and doing some basic trig on them.
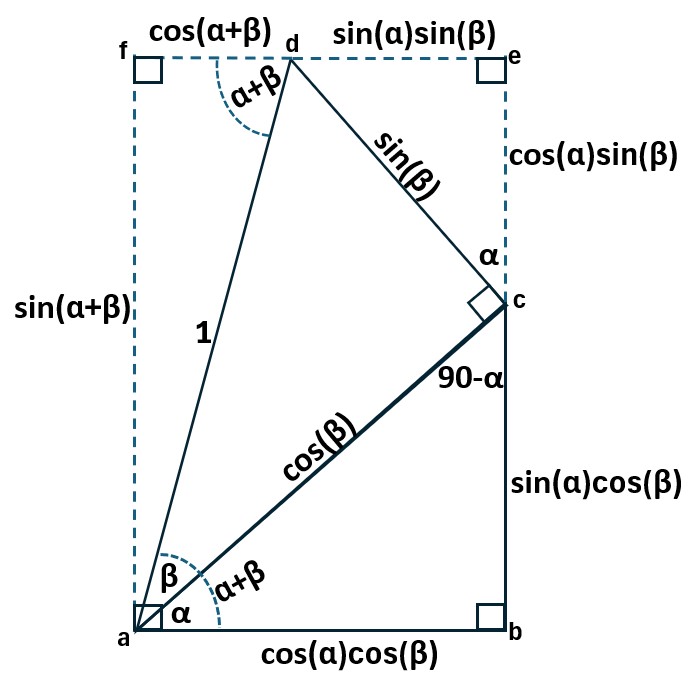
Consider the picture below as you read the set up steps.
1. Draw a right Triangle abc
2. Draw another right Triangle acd whose base is the hypotenuse of the Triangle abc
3. Designate angle cab (∠cab) as α and ∠dac as β, and ∠dab as (α+β)
4. Let the hypotenuse of Triangle acd = 1
Picture: Right Triangle Set Up for Proving Sum and Difference Angle Formulas
5. Draw perpendicular lines ce and ed such that e is at the same “height” as d.
6. Do the same to draw lines af and fd.
7. Since line ad intersects parallel lines ab and fe , their alternate interior angles are equal.
8. When a line intersects two parallel lines, the alternate interior angles are equal. Since line ad intersects parallel lines fe and ab, then angles ∠dab = α+β = ∠fda.
9. 180 degrees = ∠cab + ∠abc + ∠bca = α + 90 + ∠bca; so ∠bca = 90 – α
10. 180 degrees = ∠bca + ∠acd + ∠dce = 90 – α + 90 + ∠dce; so ∠dce = α
We can define all the sides now.
Use Right Triangle Trig Identities to Define the sides
We have the same picture below.
We can apply basic trig rules now to define the sides:
Picture: Right Triangle Set Up for Proving Sum and Difference Angle Formulas
11. Since Triangle Δacd is a right triangle with a hypotenuse of 1, then:
11.1 sinβ = opp/hyp → dc = sinβ
11.1 cosβ = adj/hyp → ac = cosβ
12. Since Triangle Δabc is a right triangle with a hypotenuse of cosβ, then:
12.1 sinα = opp/hyp → bc = sinαcosβ
12.1 cosα = adj/hyp → ab = cosαcosβ
13. Since Triangle Δdec is a right triangle with a hypotenuse of sinβ, then:
13.1 sinα = opp/hyp → de = sinαsinβ
13.2 cosα = adj/hyp → ec = cosαsinβ
14. Since Triangle Δdfa is a right triangle with a hypotenuse of 1, then:
14.1 sin(α+β) = opp/hyp → af = sin(α+β)
14.2 cos(α+β) = adj/hyp → df = cos(α+β)
Sin and Cos Angle Addition (Sum) Formulas
We’ll bring the same picture down here again.
Picture: Right Triangle Set Up for Proving Sum and Difference Angle Formulas
This rectangle has equal sides, so line fe = line ab and line fa = line eb, so
15. fe = fd + de = ab → cos(α+β) + sinαsinβ = cosαcosβ
15.1 cos(α+β) = cosαcosβ – sinαsinβ ; Cosine Angle Addition Formula
16. and fa = eb = ec + cb → sin(α+β) = cosαsinβ + sinαcosβ
16.1 sin(α+β) = cosαsinβ + sinαcosβ ; Sine Angle Addition Formula
Return to Menu
Sin and Cos Angle Subtraction (Difference) Formulas
Let’s get the difference versions of 15.1 and 16.1
In 15.1 we can substitute -β for β:
17. cos(α+-β) = cosαcos(-β) – sinαsin(-β)
but cos(-β) = cos(β) and sin(-β) = -sin(β) , so
17.1 cos(α-β) = cosαcosβ + sinαsinβ; Cosine Angle Subtraction (Difference) Formula
In 16.1 we can substitute -β for β:
18. sin(α+-β) = cosαsin(-β) + sinαcos(-β)
but cos(-β) = cos(β) and sin(-β) = -sin(β) , so
18.1 sin(α-β) = sinαcos(β) – cosαsin(β); Sine Angle Subtraction (Difference) Formula
Return to Menu
Tan Angle Addition (Sum) and Subtraction (Difference) Formulas
From the tangent trig identity, we know that,
19. tan(α+β) = opposite/adjacent = sin(α+β)/cos(α+β)
so substituting equations (17.1) and (18.1) into (19) we get,
20. tan(α+β) = (cosαsinβ + sinαcosβ)/(cosαcosβ – sinαsinβ)
Divide the Numerator and Denominator by cosαcosβ:
21. tan(α+β) = (cosαsinβ/cosαcosβ + sinαcosβ/cosαcosβ)/(cosαcosβ/cosαcosβ – sinαsinβ/cosαcosβ)
The four terms in equation (21) simplify neatly:
21.1 cosαsinβ/cosαcosβ = (1)(tanβ)
21.2 sinαcosβ/cosαcosβ = (tanα)(1)
21.3 cosαcosβ/cosαcosβ = 1
21.4 sinαsinβ/cosαcosβ = tanαtanβ
so (21) becomes
22. tan(α+β) = ((1)(tanβ) + (tanα)(1))/(1 – tanαtanβ)
or
23. tan(α+β) = (tanβ + tanα)/(1 – tanαtanβ); Tangent Angle Addition (Sum) Formula
We can get the difference version of equation 23 by repeating what we did for the sin and cos expressions.
Substitute -β for β in (23):
24. tan(α+-β) = ((tan(-β)) + (tanα))/(1 – tanαtan(-β))
Like sin, tan is an odd function, which means
25. tan(α-β) = ((-tan(β)) + (tanα))/(1 + tanαtan(β))
or
25. tan(α-β) = (tanα-tanβ)/(1 + tanαtanβ) ; Tangent Angle Subtraction (Difference) Formula
Return to Menu
Example: Cos2(x)
The derivation of the Root Mean Square (RMS) of a sinusoidal function requires solving the integral of Cos2(x).
The integration simplifies when we replace ∫cos2(wt)dt with its equality ∫1/2(1+ cos(2wt)dt.
See this great video to learn more about this RMS example : Ch 12 AC Power (23 of 58) How to Calculate the RMS Current? Michel van Biezen
We can show that cos2(wt) equal 1/2(1+ cos(2wt)) by using the cosine angle summation identity.
15.1 cos(α+β) = cosαcosβ – sinαsinβ ; Cos Angle Addition Formula
So, let’s show that cos2(wt) = 1/2(1+ cos(2wt)).
Start with cos(2x) and apply equation 15.1:
1. cos(2x) = cos(x + x) = cosxcosx – sinxsinx = cos2(x) – sin2(x)
We also know (Pythagorean identity; see my Geometry and Trigonometry Rules post) that :
2. sin2(x) + cos2(x) = 1 ; Pythagorean Identity
so
3. sin2(x) = 1 – cos2(x)
Substitute for sin2(x) in the cos(2x) expression (equation 1)
4. cos(2x) = cos2(x) – (1 – cos2(x)) = 2cos2(x) – 1
solving for cos2(x) we get,
5. cos2(x) = 1/2(cos(2x) – 1)
Lets integrate the original problem using this equality.
∫1/2(1+ cos(2wt)dt
Separate the terms and apply the basic rules of integration.
Separate the Constant and Terms:
Integrate the First Term:
Integrate the Second Term (using Substitution):
For , let
Then the derivative is
This means
Substitute into the integral:
- Substitute back : ω)sin(2ωt)
Solution:
Summary – Sin, Cos, Tan Sum and Difference Angle Formulas
cos(α+β) = cosαcosβ – sinαsinβ ; Cosine Angle Addition Formula
sin(α+β) = sinαcosβ + cosαsinβ ; Sine Angle Addition Formula
cos(α-β) = cosαcosβ + sinαsinβ ; Cosine Angle Subtraction (Difference) Formula
sin(α-β) = sinαcos(β) – cosαsin(β) ; Sine Angle Subtraction (Difference) Formula
tan(α+β) = (tanα + tanβ)/(1 – tanαtanβ) ; Tangent Angle Addition (Sum) Formula
tan(α-β) = (tanα-tanβ)/(1 + tanαtanβ) ; Tangent Angle Subtraction (Difference) Formula
Return to Menu
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
