Menu (linked Index)
The Derivative
Last Update: August 6, 2025
Introduction
This article is a high level introduction to the mathematical tool called differentiation.
At its core, differentiation is the process of finding the instantaneous rate of change of a function i.e. the exact rate of change at a single moment.
Differentiation is used to solve a wide variety of real-world problems.
Here are some real world application of differentiation:
- Physics: Calculating the velocity and acceleration of a moving object.
- Velocity is the derivative of position with respect to time, and acceleration is the derivative of velocity
- Many other physics problems involving fluid flow, electromagnetism and electrodynamics, etc.
- Engineering: Designing structures and vehicles by calculating stress, strain, and material strength.
- Economics: Determining marginal cost, marginal revenue, and marginal profit for businesses to optimize production and pricing.
- Finance: Analyzing the rate of change of stock prices or investment returns to inform trading strategies.
- Medicine: Modeling the rate at which a drug is absorbed or eliminated from the body to determine appropriate dosages.
- Biology: Predicting the growth rates of populations, such as bacteria in a petri dish or animals in an ecosystem.
- Optimization Problems: Finding the maximum or minimum value of a function.
- Can contribute heavily to value analysis in economics and finance (in all businesses)
- Computer Graphics: Creating smooth, continuous curves and surfaces for animations and 3D modeling.
- Machine Learning: Powering gradient descent, a key algorithm used to train models by minimizing an error function.
- Meteorology:
- Modeling the rate of temperature change or atmospheric pressure to help predict weather patterns.
- Wind pattern modelling
- Geography and Geology: Contour maps
In the following sections we’ll define differentiation and establish its primary rules.
The Derivative
If you want to give your brain a precious gift, go to Khanacademy.org and review some of the introductory Calculus material.
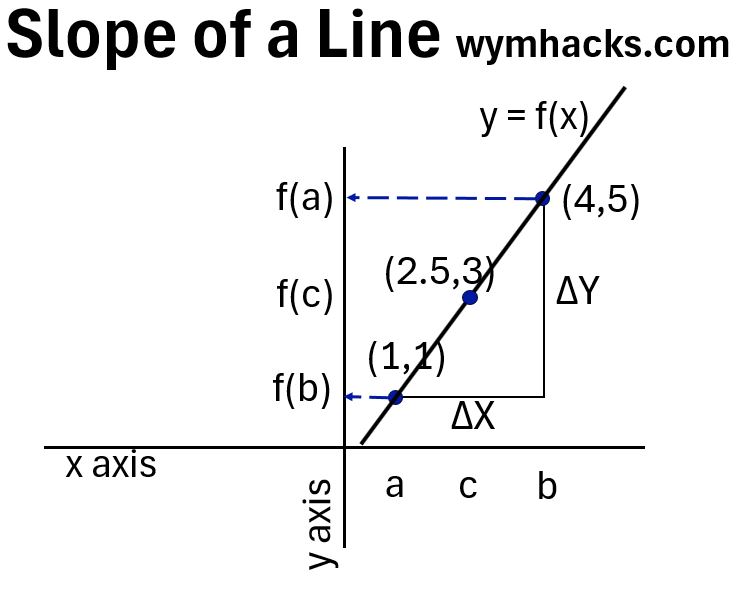
Slope of a Line
The slope of a line is the “rise over the run” i.e. (the change in y)/(the change in x) = Δy/Δx in a Cartesian coordinate system.
In the graph below, the slope of the line y = f(x) can be defined by the two points (4,5) and (1,1) where we are using (x,y) notation on a Cartesian coordinate system.
Graph_Slope of a Line y=f(x)
The slope using points a and b will be = Rise/Run
= Δy / Δx = (f(a) – f(b)) / (b-a)
= (5-1)/(4-1) = 4/3 = 1.33
Lines by definition have the same slope , so we’ll get the same slope for any other pair of points.
If we use points c and b
= (3-1)/(2.5-1) = 1.33
= (5-3)/(4-2.5) = 1.33
What if we wanted to find the slope of a curve?
Slope of a Curve
Consider the curve in the graph below.
Graph_Slope of a Curve
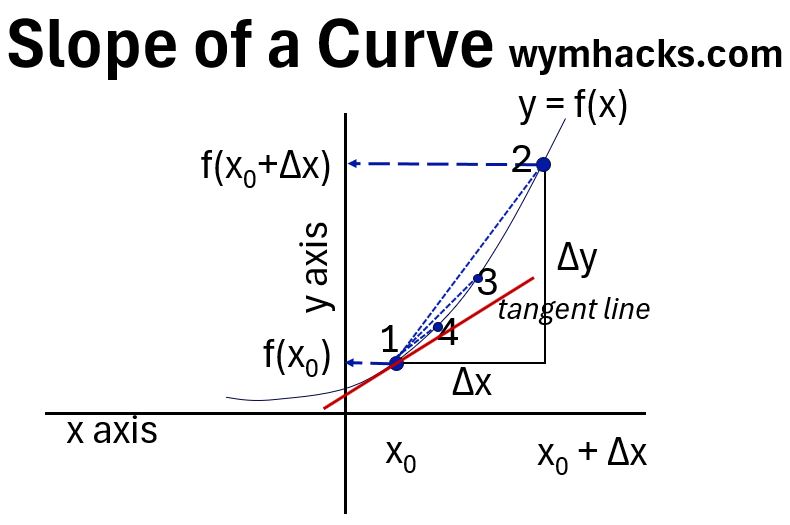
The Curve at each point has a different slope. So, What is the slope at point 1?
We still need two points to compute a slope so let’s choose Points 1 and 2 (see graph above).
- Slope 1 to 2 = Rise/Run = ∆y / ∆x
- Will give the slope of the Secant Line 12 (the dotted line between the two points in the graph)
This slope will not be very accurate.
We could compute the slope of Secant Line 13. It’ll be better but will still be off.
We could improve on this and compute the slope of Secant Line 14.
Ideally, if we could make the distance between the x points , ∆x, infinitely small, we would get the true slope at point 1.
We call this the slope of the tangent line at point 1 or the derivative of y = f(x) evaluated at point 1.
The general formula for a derivative states that
- as the limit of the difference in x values goes to zero,
- the slope will be equal to the (change in f(x))/(change in x).
or
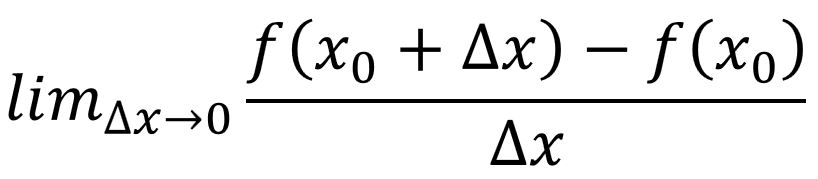
We can notate the derivative in a few ways:
- Derivative of f(x)
- f prime x or f'(x) ; Lagrange Notation
- df(x)/dx = dy/dx; Leibniz Notation
- slope of tangent line at x
For a curve, each point has a unique tangent line with a unique slope (a unique derivative).
Check out these two nice introductory videos on the derivative:
Derivative Rules
I’ve listed some of the main calculus derivative rules below.
Use Khanacademy.org’s excellent videos to learn more about these.
The primary rule for derivatives is the power Power Rule and is defined as follows:
Power Rule: d/dx(xn) = nxn-1 where n cannot be zero.
For example, the derivative of 3x3 is 3*3x2 = 9x2
Here is a summary of the main derivative rules including the Chain Rule which is very useful.
Table_Some Derivative Rules
Derivatives of Some Useful Functions
We’ll also run into some functions we’ll need to take the derivatives of.
These are equalities that you would basically have to memorize if you were taking a calculus class.
Derivatives of sin(x) ,cos(x) tan(x), cot(x), sec(x), csc(x)
- d/dx(sinx) = cosx
- d/dx(cosx) = -sinx
- !! These derivatives are only true if x is in units of Radians i.e. not degrees. ( due to the limit assumptions made in the derivations).
Note that that the derivatives of the co-functions (cosine, cosecant, cotangent) are negative.
Derivative of 𝑒ˣ
- d/dx(ex) = ex
- You can learn more at my blog on e (Euler’s Number) and ex
Derivative of ln(x)
- d/dx(lnx) = 1/x
Table_Derivatives of cosx, sinx,ex, and lnx
Ordinary Derivative
The derivatives we’ve discussed above are more properly called ordinary derivatives.
An ordinary derivative is the derivative of a function with a single independent variable ( y = f(x) )
It measures the instantaneous rate of change of the function at a specific point.
- It’s the derivative of a function whose
- domain (set of all possible input values) is one-dimensional (in R1 space), and
- whose graph is visualized in two dimensions (in R2 space).
- Notation: It’s typically written using standard derivative notation, such as or .
- Interpretation: Geometrically, the ordinary derivative at a point is the slope of the tangent line to the function’s graph at that point.
The term “ordinary” is used to distinguish it from a partial derivative, which applies to functions of multiple variables. (e.g. z = f(x,y))
An ordinary derivative deals exclusively with a function that only has one variable to begin with, while a partial derivative holds all other variables constant to measure change with respect to just one.
Partial Derivative
A partial derivative is a derivative of a multivariable function with respect to one variable, while all other variables are held constant.
- It measures the rate of change of the function along a specific axis.
- The symbol for a partial derivative is:
- The partial derivative is applied to equations that are functions of at least two independent variables. (e.g. f(x,y,..))
- For a 2 variable function f(x,y), for example,
- The domain of input variables is in the 2 dimensional the xy plane (R2).
- The graph of the function is in the 3 dimensional R3 space.
How to Calculate a Partial Derivative
- Identify the variable you’re differentiating.
- Treat all the other variables as constants.
- Differentiate by applying the rules of differentiation.
Example Partial Differentiation
Consider a function with two variables,
Partial Derivative with Respect to
To find the partial derivative with respect to
- ∂/∂x(
- ∂/∂x(sin(
So, ∂/∂x() = 2xy + 0 = 2xy
Partial Derivative with Respect to
To find the partial derivative with respect to constant):
- ∂/∂y(
- ∂/∂y(sin(
So, ∂/∂y() =
Formal Definition of a Partial Derivative
For a multivariable function f(x,y,..), the partial derivative of the function with respect to its variables x, y, z.. is:
- ∂x (a,b,c,..) = lim h→0 [ (f(a+h,b,c) – f(a,b,c..))/h ]
- ∂y (a,b,c,..) = lim h→0 [ (f(a,b+h,c) – f(a,b,c..))/h ]
- ∂z (a,b,c,..) = lim h→0 [ (f(a,b,c+h) – f(a,b.c..))/h ]
- etc..
where
- (a,b,c,..) is some point in two (R2), three (R3), or higher dimensional space.
- h is an infinitesimal change in the direction of x or y or z or etc..
and
- Each partial derivative is a separate result that measures the instantaneous rate of change of the function with respect to one specific variable, while holding all other variables constant.
The number of partial derivatives you can calculate is equal to the number of variables in the function’s domain.
Check these great Grant Sanderson Khanacademy videos.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.
