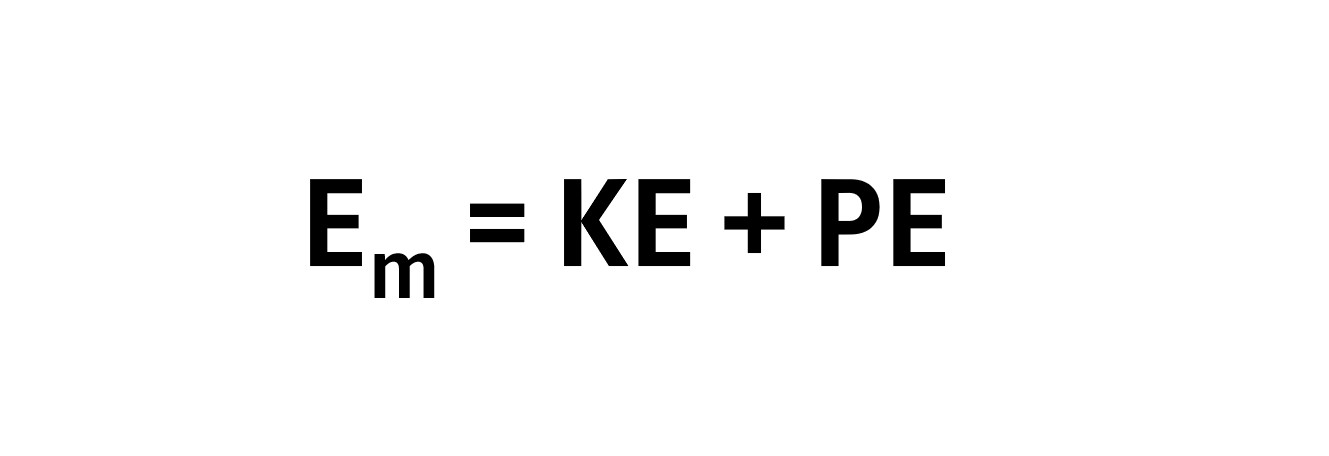Menu (linked Index)
Work and Energy
Last Update: October 28, 2025
Introduction
In this post we’ll review some fundamental principles that govern motion and energy in our universe.
The exploration begins with the Work Equation, to understand how forces transfer energy.
We’ll then develop the Kinematic Equations, which will allow us to develop the concept of Kinetic Energy.
We’ll then review Gravitational Potential Energy, the stored energy of position.
I’ll show a simple example of how the Law of Conservation of Mechanical Energy can be applied using these concepts.
I’ll also explore and develop the Spring Force equations (Hooke’s Law).
Things will then get a little more complicated (but interesting!!) when I try to relate Conservative Forces and Potential Energy to the four Fundamental Forces.
I’ll wrap it up by developing a few more work and mechanical energy relationships.
Let’s get started!
Some Great Khan Academy Resources
The links below get you to some great Khanacademy videos because
- Sal Khan,
- Mahesh Shenoy, and
- David SantoPietro
are great teachers.
Watch them.
Work
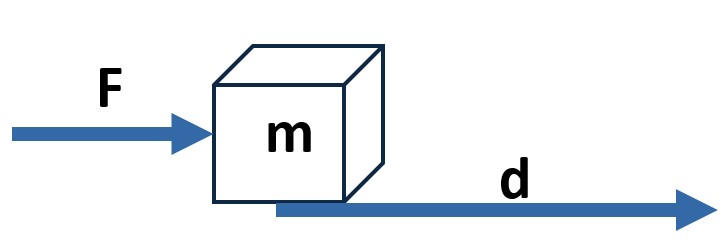
Consider a block of mass m being moved a distance d by a net force F.
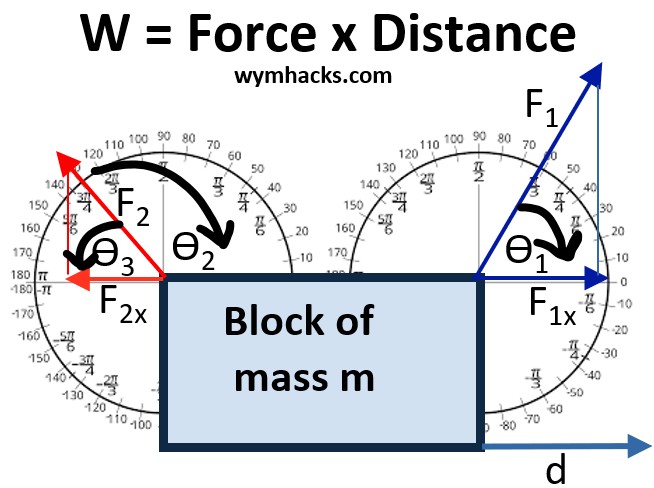
The work done on the block, W, is done by the component of the force that is in the same direction (or reverse direction) of the movement.
Work = W = Fcos(θ)d
- F is the magnitude of the force
- d is the magnitude of the displacement.
- θ = angle between force and displacement vector (having direction and magnitude)
- cos(θ) in a right triangle = (Length of side Adjacent to θ)/(Length of Hypotenuse)
- Fcos(θ) = is the component of the force in the direction of the displacement
In the example shown in the picture above, there are two force components that result in the block moving to the right a distance d.
- Work1 = F1cos(θ1)d = F1xd
- Work2 = F2cos(θ3)d = F2cos(180-θ2)d = –F2xd
- Net Work = (F1x–F2x)d
Angle implication on force:
- When θ=00: The force is in the exact same direction as the displacement.
- cos(00)=1, so W=Fd. The entire force contributes to the work.
- When θ=1800: The force is in the exact opposite direction of the displacement.
- cos(1800)=−1, so W=−Fd. In this case, the work done is negative, meaning the force is opposing the motion (e.g., friction).
- When θ=900: The force is perpendicular to the displacement.
- cos(900)=0, so W=0. No work is done by this force (e.g., the normal force on a horizontally moving object).
The component of the force that does the work is the component that is parallel to the direction of the displacement (either in the same direction, resulting in positive work, or in the opposite direction, resulting in negative work).
Any component of the force perpendicular to the displacement does no work.
No displacement also results in no work.
Kinematic Equations
See this great video by Mahesh Shenoy at Khanacademy: Deriving 3 equations of motion (from v-t graph)
The Work-Energy Theorem states that
- The net work done on an object is equal to the change in its kinetic energy.
We want to develop the equation form of this statement but we don’t have all the tools yet.
We first need to develop the Kinematics Equations in order to do this.
Linear Kinematic Equations
Kinematics equations
- describe the motion of objects with constant acceleration.
- relate distance (displacement), time, initial velocity, final velocity, and acceleration.
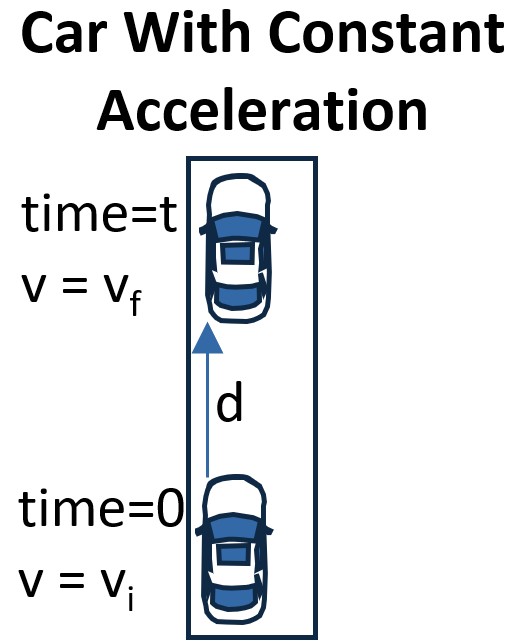
I want to derive them from the simple example of a car with
- constant acceleration
- at initial velocity vi at time zero
- and final velocity vf
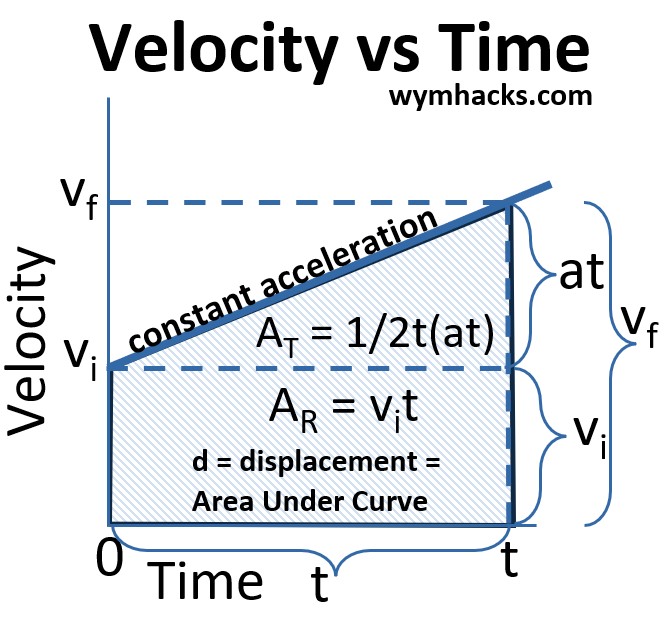
Plotting velocity versus time, we get the chart below.
Let a = acceleration = ∆v/∆t
(1) a = (vf -vi)/t
Solve for vf:
(2a) vf =vi + at ; Linear Kinematic Equation
Solve (2) for t:
(3) t = (vf -vi)/a
Let d =
-
- distance travelled
- = displacement
- = velocity x time
- = area under the curve
- = area of a trapezoid
- = 1/2(base1 + base2)height
The area of the shaded region in the graph is therefore,
(4a) d = 1/2(vi +vf)t ; Linear Kinematic Equation
The area can also be computed as the sum of the areas of the rectangle and triangle in the shaded region:
(5) d=vit + 1/2t(at)
(6a) d=vit + 1/2at2 ; Linear Kinematic Equation
Substitute (3) into (4):
(7) d = 1/2(vi +vf)(vf -vi)/a
(8) d = 1/(2a)(vf2– vi2)
Rearranging,
(9a) (vf2-vi2) = 2ad ; Linear Kinematic Equation
Equations 2, 4, 6, and 9 are called the Linear Kinematic Equations and only apply in constant velocity or constant acceleration situations.
These each can be used to compute a motion related variable if three of the four variables are known.
Rotational Kinematic Equations
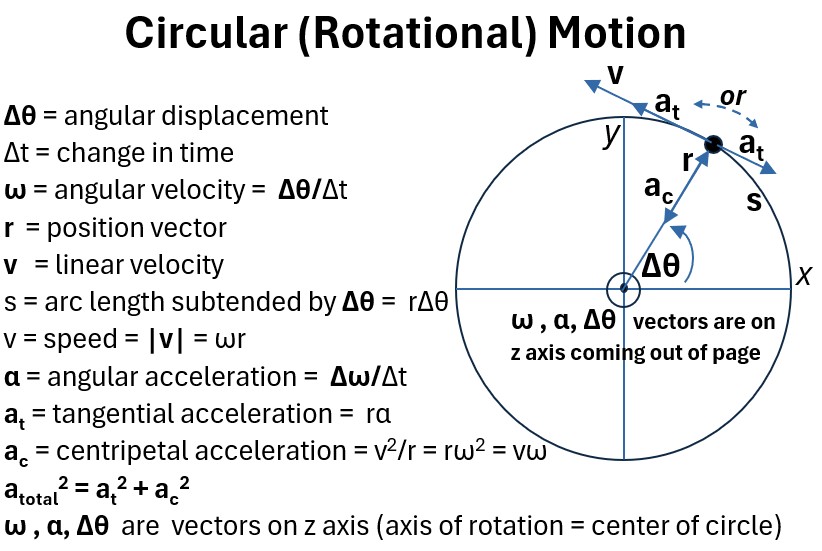
See my post Rotational Motion Variables for a thorough discussion of the rotational variables shown in the picture below.
Using the same methodology we can derive analogous kinematic Equations for rotational motion (valid only when angular acceleration α is constant).
Picture: Rotational Motion , XY plane, Counterclockwise Example
The four rotational kinematic equations analogous to linear equations (2a), (4a), (6a), and (9a) are:
(2b) ω = ω0 + αt ; Rotational Kinematic Equation
(4b) θ – θ0 = 1/2(ω0 + ω)t ; Rotational Kinematic Equation
(6b) θ = θ0 + ω0t + 1/2αt2 ; Rotational Kinematic Equation
(9b) ω2– ω02 = 2α(θ – θ0) ; Rotational Kinematic Equation
where
- ω; ω0 = final and initial angular velocity
- α = angular acceleration
- θ; θ0 = final and initial angular displacement
Kinetic Energy
Lets apply a force F on a block of mass m in the direction of distance d for a certain distance d.
Picture: Moving Block with Mass m a Distance d
We want to compute the velocity of the block after its travelled the distance d.
Start with,
1. W = Fd
Kinematic equation 9 from the previous section is
2. (vf2-vi2) = 2ad
- where a is the acceleration
- and d is the distance travelled
Because F = ma, we can express a as
3. a = F/m
Assuming vi = 0, and substituting for a, equation 2 becomes
4. vf2 = 2ad = 2(F/m)d = 2(Fd)/m = 2W/m
where W = work.
So
5. vf = v = sqrt (2Fd/m)
We can also adjust equation 4 and get an interesting equation for W
6. W = (1/2)mv2
Equation 6 is the equation for kinetic energy.
We see that
7. W = Fd = (1/2)mv2 = kinetic energy
We see that that the work we applied to move the block of mass m from rest to a final velocity is equal to the kinetic energy of the object.
Equation 7 is sometimes referred to as the Work Energy Theorem.
Gravitational Potential Energy
Picture: Lifting a Block of Mass m
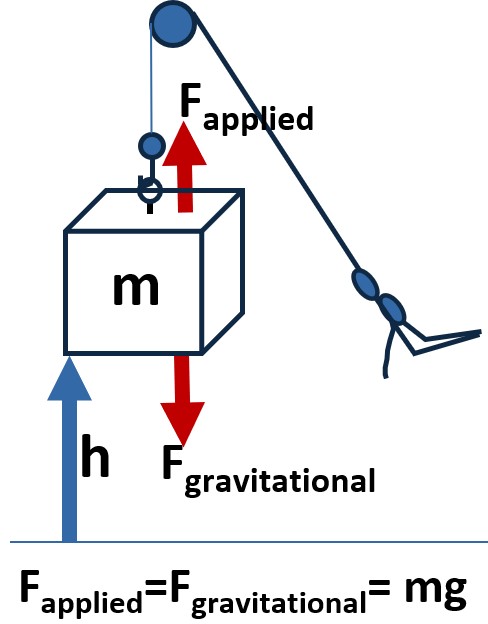
The block is now suspended and not moving at height h.
For the block to remain suspended at height h the applied force upwards has to equal the downward force of gravity.
Lets derive the gravitational force expression (mg) that I show in the picture.
We have to start with Newton’s Law of Universal Gravitation:
- Fg = G(m1)(m2)/r2
- Fg = gravitational force
- G= universal gravitational constant = 6.67e-11 Nm/kg2
- m1, m2 = mass of objects 1 and 2
- r = distance between objects (don’t confuse with radius)
- Let’s reconfigure the equation to apply to an object on earth.
- Fg = G(m1)(m2)/r2
- Let m1 = mass of earth and m2 = m = mass of object on earth where
- m1 = mass of earth = ~5.97e24 kg
- r = distance from center of object on surface (or “near” surface…see Note below) of earth to center of the earth = ~6378 km
- so, Gm1/r2 = [(6.67e-11 Nm/kg2)(5.97e24 kg)]/(6378 km)2 = g = ~ 9.8 m/s2
- Fg = mg = Gravitational Force between earth and object with mass m
- g = acceleration of gravity for earth (~9.8 m/s2)
- Note, for objects further away from the earth (e.g. satellites), Gm1/r2 wont be “g” anymore as r becomes significantly larger than the earths radius
- Note, the more general form of
So, knowing what we know, what work as been done on the block?
- W = Force * Distance and we know that the applied force has to equal the force of gravity on the block for it to remain suspended at that height.
- and from Newtons Law of Universal Gravitation, we have an expression for Fgravitational
- W =Fapplied* height = Fgravitational * height = (mg)(h) = mgh
W = mgh = gravitational potential energy
Gravitational potential energy is the energy an object possesses due to its position within a gravitational field.
It’s a form of stored energy that has the “potential” to be converted into kinetic energy (energy of motion) if the object is allowed to fall or move under the influence of gravity.
Law of Conservation of Energy
Energy cannot be created or destroyed; just transformed.
Remember also that E = mc2 a i.e. the equivalence of mass and energy.
Even with mass-energy equivalence, the core idea holds:
- energy doesn’t just vanish into nothing, nor does it appear from nothing.
- It’s always accounted for, either in a different form of energy or as a change in mass.
Consider a block that we drop down an uneven hill, that we say is frictionless.
- Assuming no friction allows us to ignore other forms of energy (that we have to account for) but still make our point.
The Law of Conservation of Energy allows us to compute the velocity of the block at any point on its path downwards.
Picture: Block Sliding Down a Hill
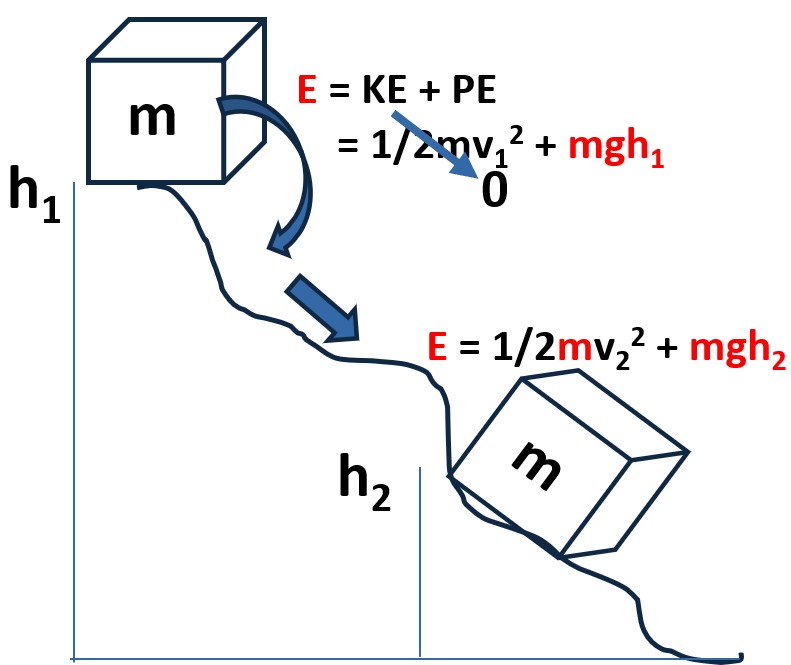
The red fonted variables in the picture above are known.
Since
- we know the total energy E and
- we know it is conserved, then
- we can compute the velocity v2 at h2
Spring Forces (Hooke’s Law)
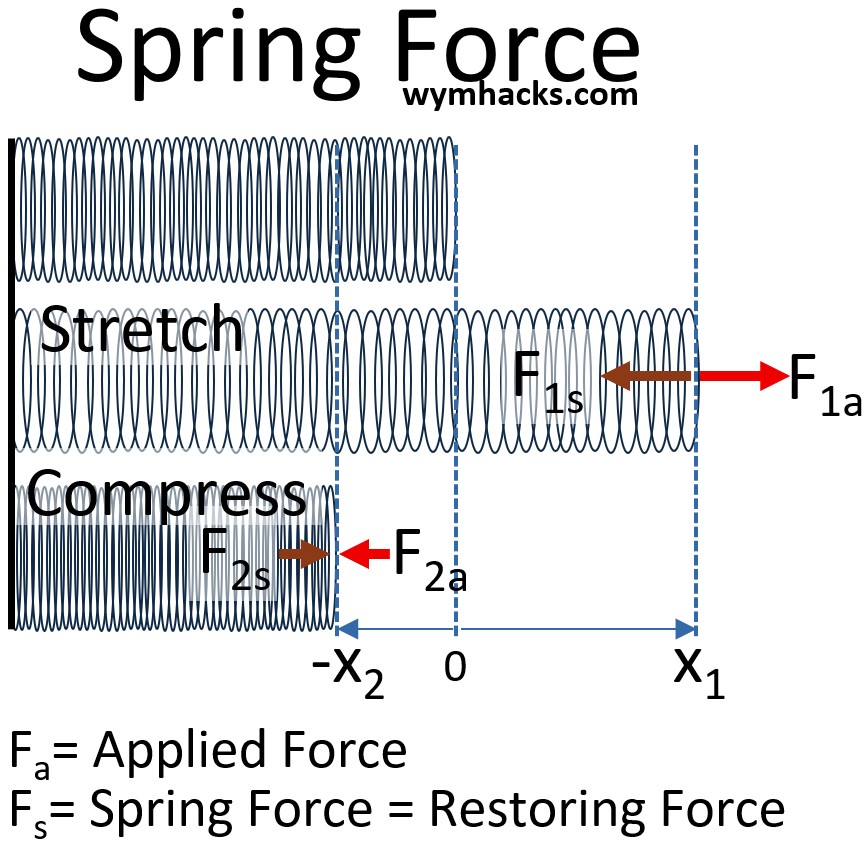
Imagine we have a spring and we stretch it and compress it.
- We can apply a pulling force and stretch the spring.
- We can apply a pushing force and compress the spring as well.
The picture below depicts this.
Picture: Spring Forces
Hooke’s law describes these actions.
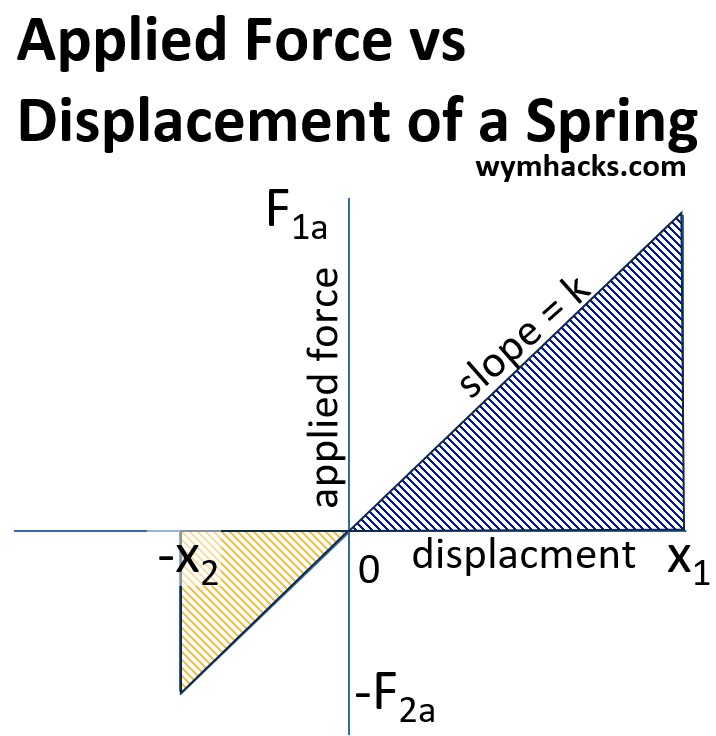
Graphing the Applied Force on a Spring
In the lab we can the measure the force it takes to stretch or compress a spring.
If we plot the force measured for a given displacement, we would (ideally) get a graph like the one below.
I say ideally because springs have deformation (elastic) limits.
- If you stretch or compress the spring too far, it will undergo plastic deformation.
- The Force vs displacement line will then begin to curve.
Graph: Spring Applied Force vs Displacement Graph
The Spring Force Equation
The graph above suggest a simple relationship between the force and the displacement and indeed there is.
The Spring Force Equation, also known as Hooke’s Law, is:
Fs =−kx
Where:
- F is the restoring force exerted by the spring.
- k is the spring constant
- k is a positive value unique to each spring, representing its stiffness.
- A higher k means a stiffer spring.
- x is the displacement of the spring from its rest position.
- It’s how much the spring is stretched or compressed.
- By convention, x is positive if the spring is stretched and negative if compressed
The negative sign indicates that the spring’s restoring force is always in the opposite direction to the displacement.
- If you stretch a spring (positive x), it pulls back (negative F).
- If you compress a spring (negative x), it pushes outward (positive F).
Hooke’s Law is an approximation that
- holds true only for deformations within the spring’s elastic limit.
- Beyond this limit, the spring may be permanently deformed or break.
Other names for the spring force are:
- Hooke’s Law force
- Restoring force
- Elastic force:
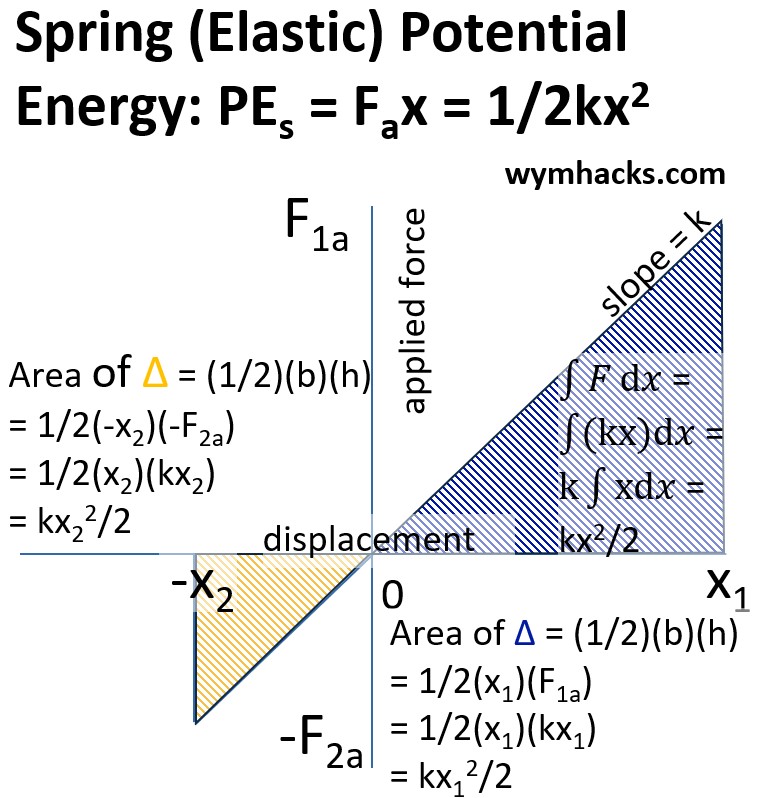
Work Done on The Spring
We know that work is defined as a force applied over a distance: (W = Force x Distance)
When you compress or stretch a spring, you
- apply a force that acts in the direction of the spring’s displacement (the compression).
- apply a force that acts in the direction of the spring’s displacement (the extension).
This work done on the spring is stored as spring (or elastic) potential energy within the spring.
- i.e. The spring has the “potential” to do work itself as it returns to its equilibrium state.
- The spring potential energy can be computed as the triangle area created by F vs displacement (see graph below)
- The spring potential energy can be computed as the mathematical integral of Fdx (see graph)
Graph: Spring (Elastic) Potential Energy – Area of the Fx (or Fdx) Triangle
So,
The Spring (Elastic) Potential Energy equation is:
PEs=kx2/2
Where:
- PEs is the Elastic (Spring) Potential Energy.
- k is the spring constant
- x is the displacement of the spring from its rest position.
Conservative Forces
A Conservative Force is a force for which
- work done in moving an object between 2 points
- is independent of the path taken.
- A Conservative Force is inherent because
- It arises directly from the fundamental nature of the objects and their interaction,
- without external intervention or dissipation.
- The force is built into the system’s configuration.
- A Conservative Force is an instantaneous property (of the field/interaction).
- The force exerted at any given point in space depends only on the position of the object at that instant.
- It doesn’t depend on the path taken to get to that position or
- the velocity of the object or
- How long the force has been acting.
This is precisely why we can define a potential energy for conservative forces.
The potential energy at a given point in space (relative to a reference point) is solely a function of position.
- The work done by a conservative force moving an object between two points is simply the negative change in this potential energy, regardless of the path
Summary of The Characteristics of A Conservative Force
- Path Independent
- The work done is independent of the path taken.
- Zero Work in Closed Loop
- The work done by a conservative force on an object moving around any closed path (returning to its starting point) is zero.
- Associated with Potential Energy
- A potential energy function can be defined for a conservative force.
- Energy Conservation (in isolated systems)
- When only conservative forces do work, the total mechanical energy (kinetic + potential) of the system is conserved.
- Reversible Work
- The work done by a conservative force is reversible; the energy transferred can be completely recovered.
Examples of Conservative Forces
Gravitational Force
The gravitational force between two masses is inherent.
- This is one of the 4 Fundamental Forces.
- It exists simply because there are masses and they are at a certain distance from each other.
- Newtons Law of Gravitational Motion defines the gravitational force
-
Fg = Gm1m2/r2
- Fg = gravitational force
- G= universal gravitational constant = 6.67e-11 Nm/kg2
- m1, m2 = mass of objects 1 and 2
- r = distance between objects (don’t confuse with radius)
-
Potential Gravitational Energy Equation
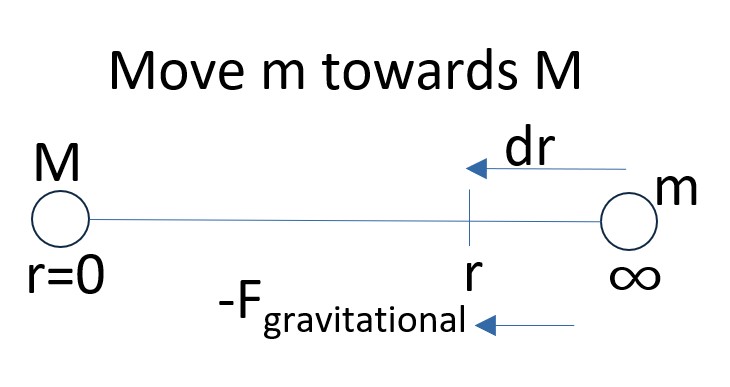
Consider the drawing below where we want to
- Infinitesimally move (test) mass m closer to (source) mass M by dr.
Picture: Move Test Mass m to Source Mass M
- Work = ∫∞r Fdr = ∫∞r -G(m)(M)/r2dr
- Integral of 1/r2 is -1/r, so
- Work = W = GmM/r
- If only conserved forces are in play, then W = -Potential Energy. So,
-
PEg = – GmM/r = Gm1m2/r
- Intuitively you can get to the result without doing all the math if
- you assume that the force is constant and
- you know work = force x distance so, GmM/r2 * r = GmM/r
Electrostatic Force
The electrostatic force between two charges is inherent.
- It exists due to the two charges and their separation.
- This is a component of the Electromagnetic Fundamental Force.
- Coulomb’s law defines the Electrostatic Force.
- Electrostatic force (Coulomb’s law)
-
Fe = kq1q2/r2
- Fe = electrostatic force
- q1, q2 =The quantity of charge of objects 1 and 2
- r = distance between the charges.
-
Potential Electrostatic Energy Equation
Consider the drawing below where we want to
- Infinitesimally move (test) charge q closer to (source) charge Q by dr.
- We can do this for like charged or oppositely charged particles.
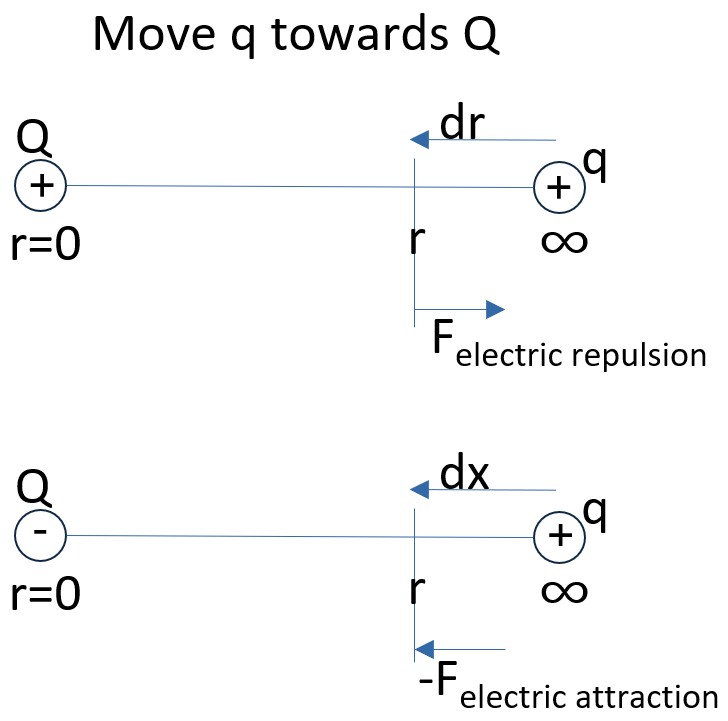
- Lets do the math for like charged particles.
- Work = ∫∞r Fdr = ∫∞r +kqQ/r2dr
- Integral of 1/r2 is -1/r, so
- Work = W = -kqQ/r
- If only conserved forces are in place, then W = -Potential Energy. So,
-
PEe = kQq/r = kq1q2/r
- Intuitively you can get to the result without doing all the math if
- you assume that the force is constant and
- you know work = force x distance so, KqQ/r2 * r = KqQ/r
- You’ll get the same result if you do the oppositely charge particle example.
Ideal Spring Force
The restoring force of an ideal spring is inherent in its stretched or compressed state, a property of its material and geometry.
We’ve already derived the Force and Potential Equations for springs:
Fs =−kx = Spring Force
PEs=kx2/2 = Spring (Elastic) Potential Energy
The examples above are typically provided in high school and even college physics texts as work (potential energy) produced by Conservative Forces.
Now, let’s broaden our view and look at conservative and Non – Conservative forces from the perspective of the four Fundamental Forces.
In order to understand Fundamental Forces a little better, you can read my article on Standard Particle Physics here.
Fundamental Forces and their Emergent Macroscopic Forces
Consider the chart below where I categorize various ’emergent’ macroscopic forces under one of the four Fundamental Forces.
Chart: Fundamental Forces and Emergent Macro Forces
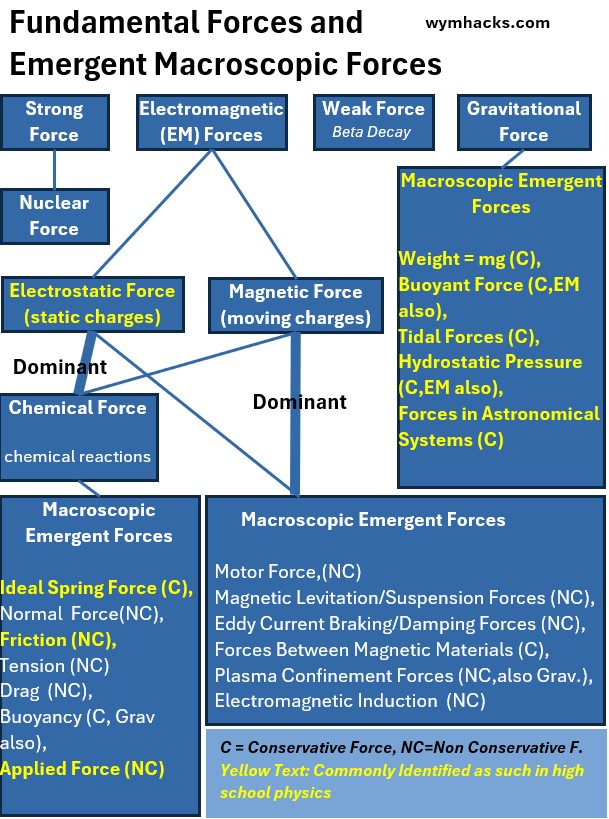
The Gravitational Force
Emergent Gravitational Forces fit well with the classical definition of Conservative Forces and are associated with the Gravitational Potential Energy as I described in an earlier section:
PEg = – GmM/r = Gm1m2/r
Now it gets a little murkier.
The Electromagnetic Force (EM Force)
This one is a bit more complicated since the EM force is a combination of electric and magnetic forces.
- The Electromagnetic Force is one of the four fundamental forces.
- It governs the interactions between electrically charged particles.
- It’s responsible for all chemical and biological processes, including how atoms bond to form molecules, the structure of matter, and how light interacts with matter.
- The EM Force underlies electricity, magnetism, and light itself,
- forming the basis for technologies like electric motors, generators, radios, and all electronic devices.
The two emergent Electromagnetic Forces are the Electrostatic Force and the Magnetic Force.
- The Electrostatic Force , as we discussed above, is a conserved force
- PEe = kQq/r = kq1q2/r
- but the magnetic force is typically not (charges have to be moving).
- for many systems governed by EM forces there will be a complicated interplay between electrical and magnetic forces.
- I try to show this complexity in the chart above.
The Strong Force
The Strong Force is associated with potential energy (nuclear binding energy)
- because it holds quarks within nucleons and nucleons within atomic nuclei.
- Energy is released when these particles bind.
However, the Strong Force is not considered a classical Conservative Force because it doesn’t follow the path independence requirement of conservative forces as defined by classical physics.
Weak Force
The Weak Force
- is associated with potential energy because
- it mediates processes like beta decay, where
- an unstable nucleus (higher potential energy) transforms into a more stable configuration (lower potential energy),
- releasing the difference as energy (kinetic energy of particles and changes in mass-energy).
- This stored energy is crucial for nuclear stability.
- However, it is not considered a classical Conservative Force because:
- it doesn’t follow the path independence requirement of conservative forces as defined by classical physics.
More on the Law of Conservation of Energy and the Mechanical Energy Equation
In the Law of Conservation of Energy section we introduced the following equation:
(1) Mechanical Energy = Em = KE + PE
Where KE and PE are the macroscopic kinetic and potential energy respectively.
We can define the change in Mechanical Energy as:
(2) ΔEm =ΔKE + ΔPE
Recall the Work Energy Theorem:
(3) W = (1/2)mv2 = KE = kinetic energy (Work Energy Theorem)
The Work Energy Theorem relates the net work done on an object to its change in kinetic energy, along a path from point 1 to point 2.
Let
(4) Wnet = ΔKE = KE2 – KE1
and let
(5) Wnet = Wc + Wnc
Where
Wc = Work done by a Conservative Forces
Wnc = Work done by Non – Conservative Forces
We know that Wc is equal to the potential energy:
(6) Wc = – ΔPE
Substitute (6) into (5)
(7) Wnet = -ΔPE + Wnc
Re-arrange.
(8) Wnc = Wnet + ΔPE
Substitute (4) into (8)
(9) Wnc = ΔKE + ΔPE
So, the work done by Non – Conservative Forces is equal to the sum of the changes in potential and kinetic energies.
But we know from equation (2) that the right hand side of (9) is equal to the change in the mechanical energy of an object:
(10) Wnc = ΔEm
So, Non – Conservative Force work = the change in the Mechanical Energy of a system.
Equation (10) says energy is conserved
(11) 0 = –Wnc + ΔEm
If there are no Non – Conservative forces doing work on the object:
(12) Wnc = ΔEm = 0 = ΔKE + ΔPE (no Non – Conservative Forces)
This is generally called the “Conservation of Mechanical Energy”.
- i.e. If there are no Non – conservative forces doing work on an object, its mechanical energy is conserved (i.e. constant).
We can simplify equation (12) to
(13) ΔKE = – ΔPE (for no Non – Conservative Forces)
That is,
- the sum of the changes in potential and kinetic energies of the object is always zero.
- If the potential energy of the object increases, then the kinetic energy of the object decreases by the same amount.
In another blog I describe how you can derive these mechanical energy equations from the First Law Of Thermodynamics.
Disclaimer: The content of this article is intended for general informational and recreational purposes only and is not a substitute for professional “advice”. We are not responsible for your decisions and actions. Refer to our Disclaimer Page.